1014-最佳观光组合

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:24 2023-09-13 16:06:24 Updated    

给你一个正整数数组 values，其中 values[i] 表示第 i 个观光景点的评分，并且两个景点 i 和 j 之间的 距离
为 j - i。

一对景点（i < j）组成的观光组合的得分为 values[i] + values[j] + i - j ，也就是景点的评分之和 减去
它们两者之间的距离。

返回一对观光景点能取得的最高分。

示例 1：

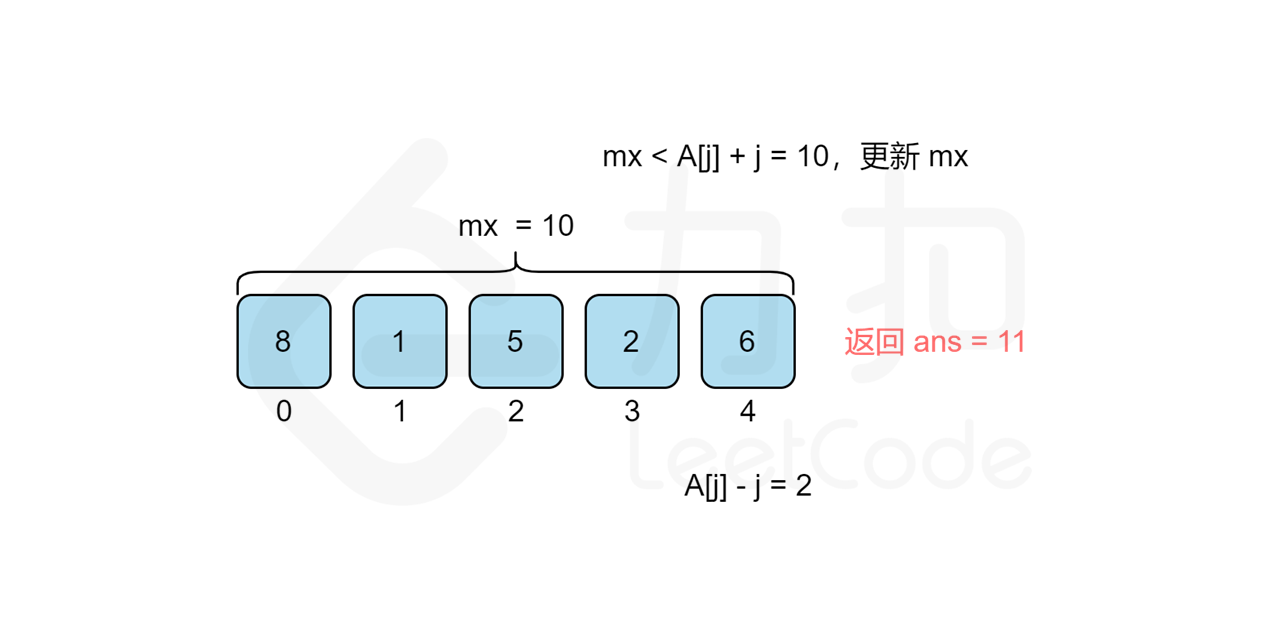
**输入：** values = [8,1,5,2,6]
**输出：** 11
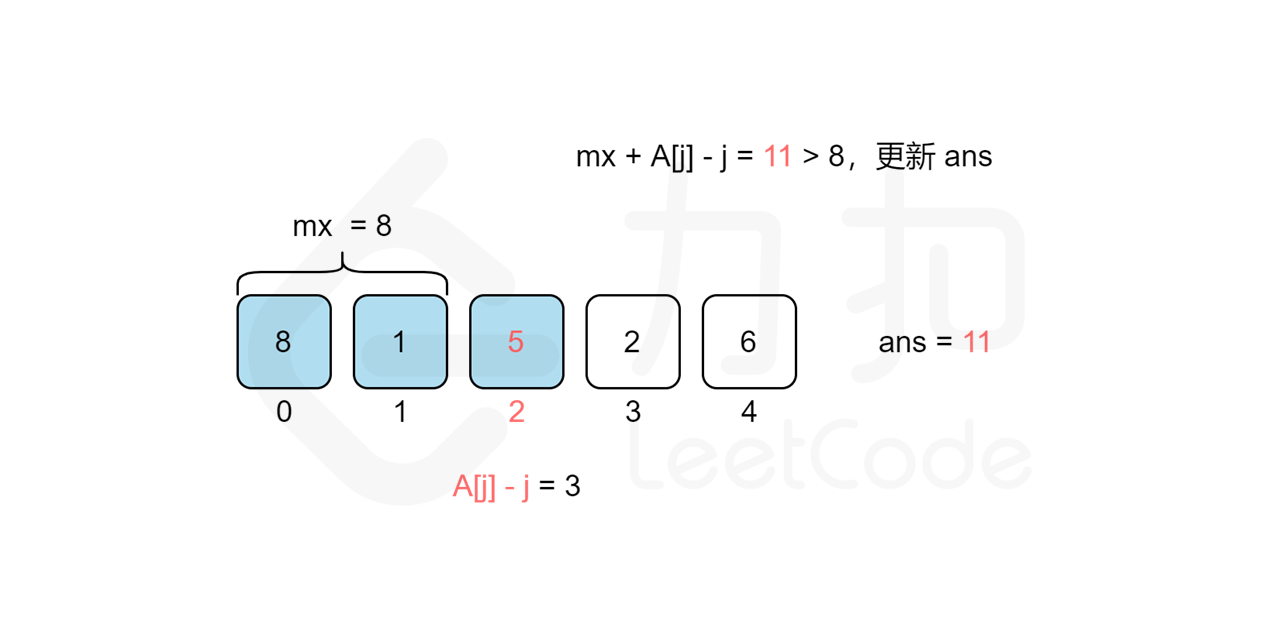
**解释：** i = 0, j = 2, values[i] + values[j] + i - j = 8 + 5 + 0 - 2 = 11

示例 2：

**输入：** values = [1,2]
**输出：** 2

提示：

  • 2 <= values.length <= 5 * 104
  • 1 <= values[i] <= 1000

方法一：遍历

思路和算法

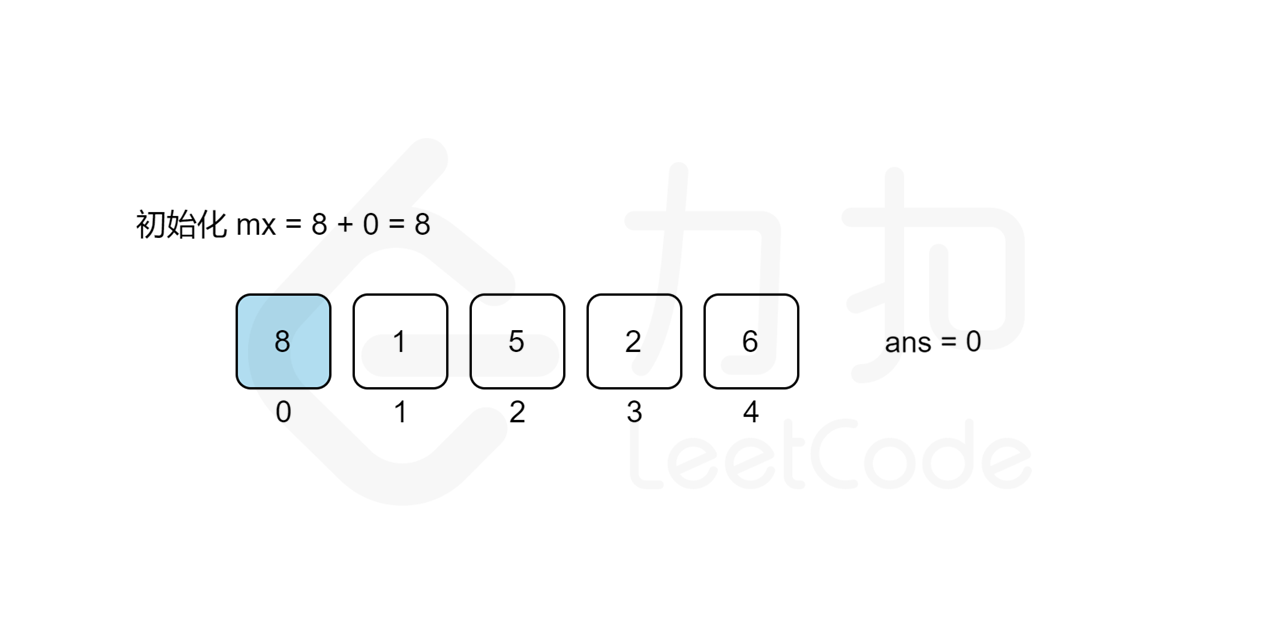
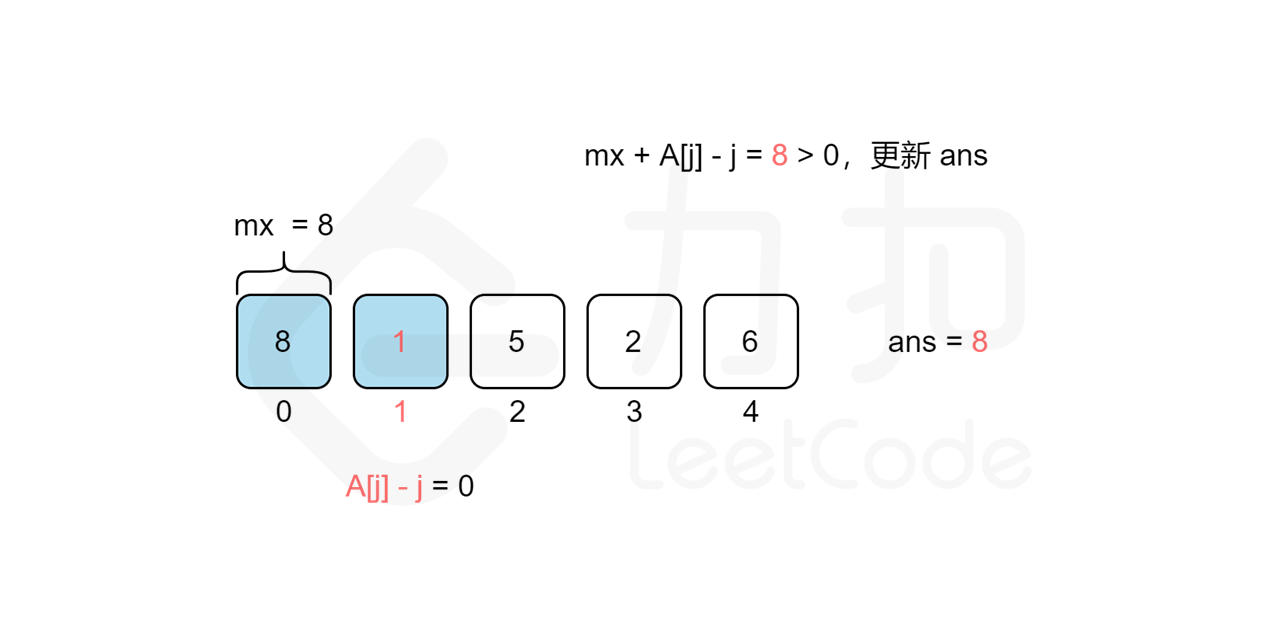
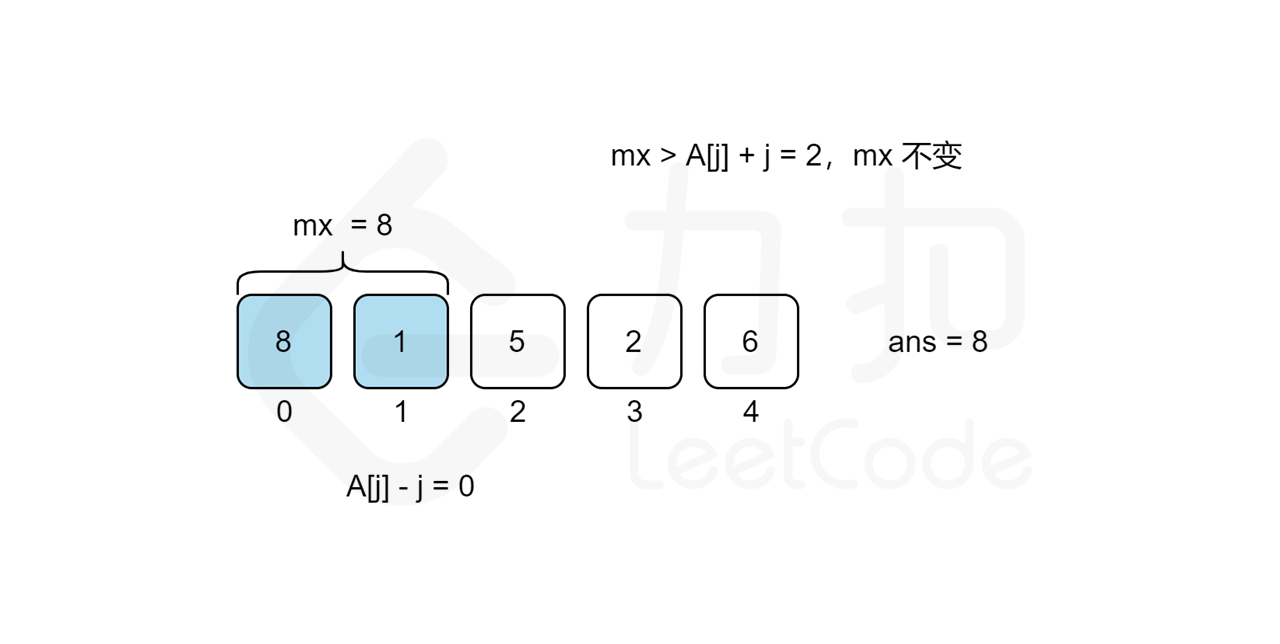
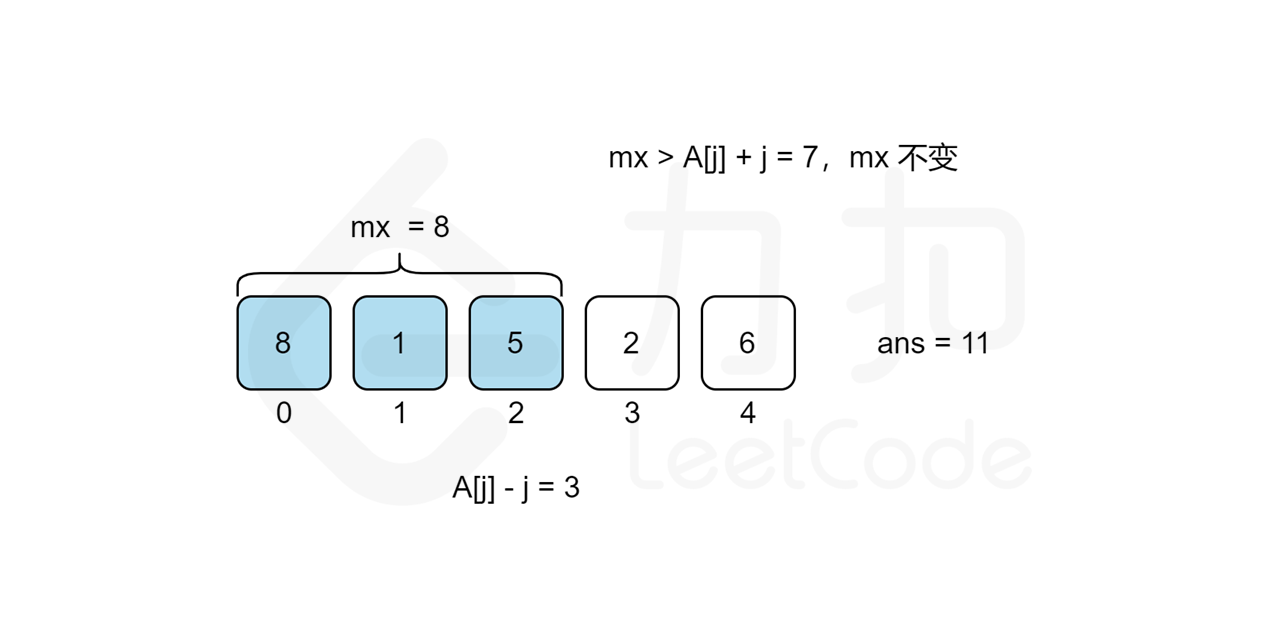
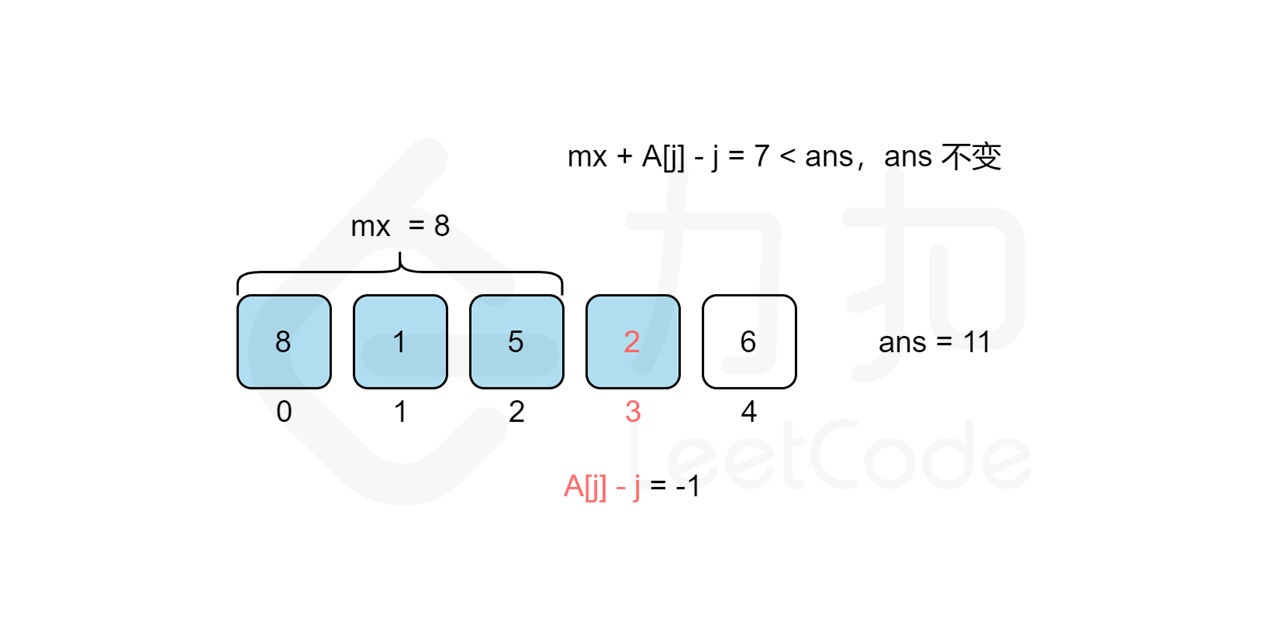
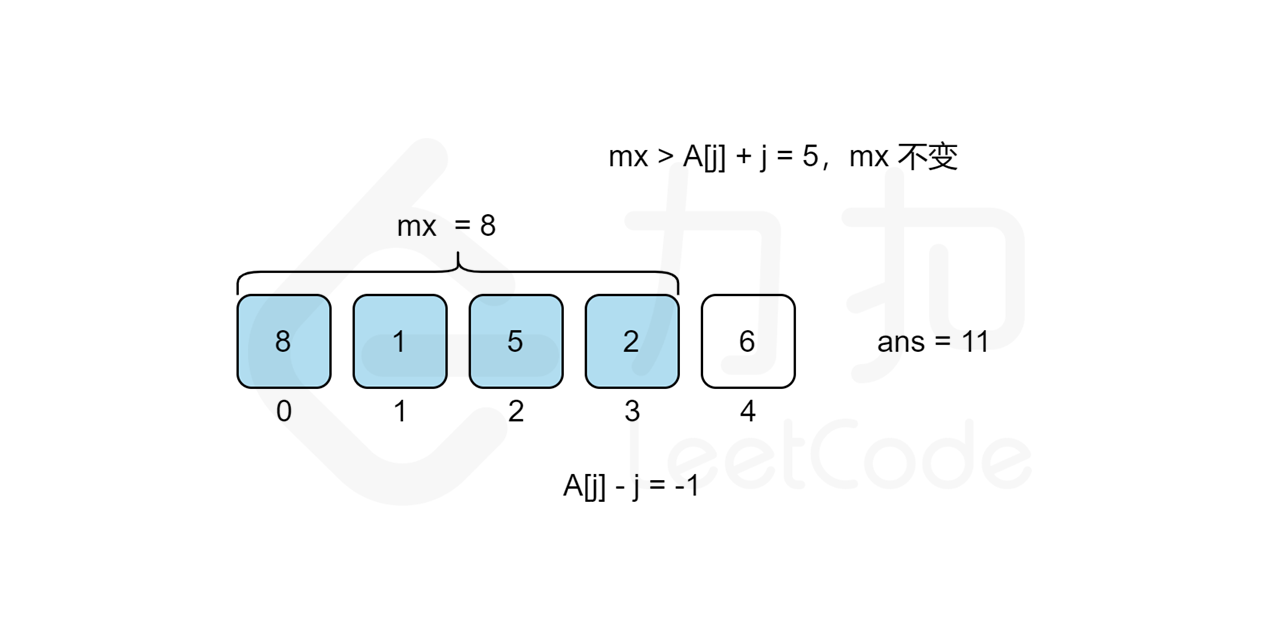
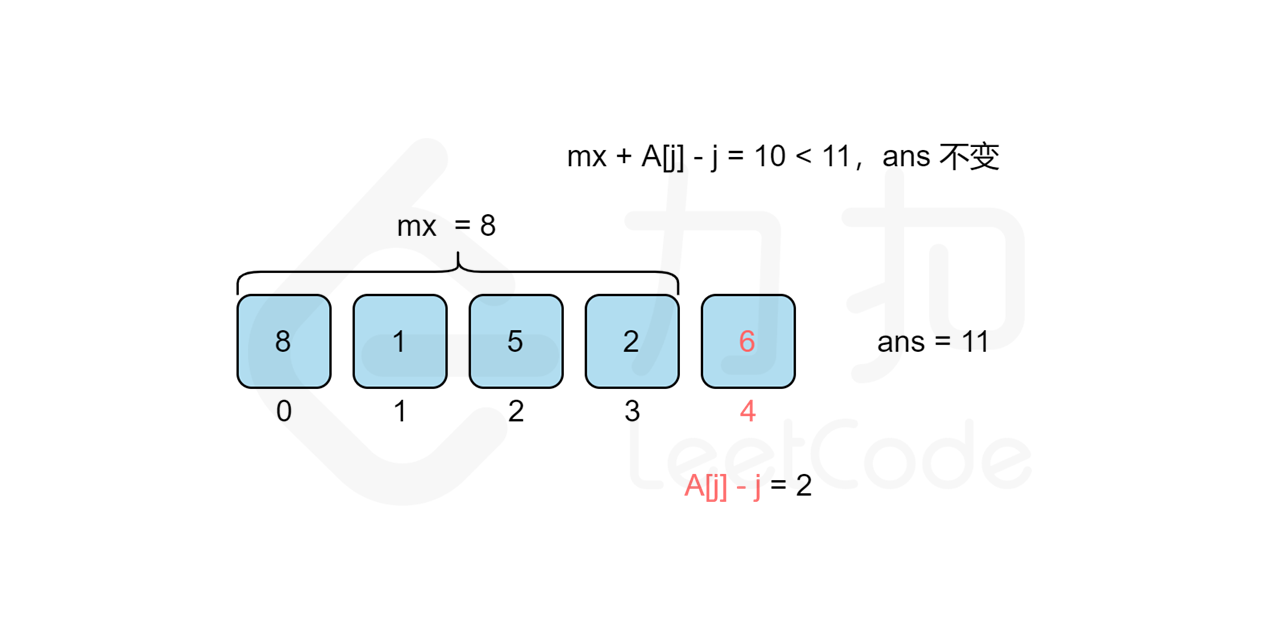
我们考虑从前往后遍历 j 来统计答案，对于每个观光景点 j 而言，我们需要遍历 [0,j-1] 的观光景点 i 来计算组成观光组合 (i,j) 得分的最大值 cnt}j 来作为第 j 个观光景点的值，那么最后的答案无疑就是所有观光景点值的最大值，即 \max{j=0..n-1}{cnt_j\。但是遍历 j 需要 O(n) 的时间复杂度，遍历 [0,j-1] 的观光景点 i 也需要 O(n) 的时间复杂度，因此该方法总复杂度为 O(n^2)，不能通过所有测试用例，我们需要进一步优化时间复杂度。

我们回过头来看得分公式，我们可以将其拆分成 values}[i]+i 和 values}[j]-j 两部分，这样对于统计景点 j 答案的时候，由于 values}[j]-j 是固定不变的，因此最大化 values}[i]+i+\textit{values}[j]-j 的值其实就等价于求 [0,j-1] 中 values}[i]+i 的最大值 mx，景点 j 的答案即为 mx}+\textit{values}[j]-j 。而 mx 的值我们只要从前往后遍历 j 的时候同时维护即可，这样每次遍历到景点 j 的时候，寻找使得得分最大的 i 就能从 O(n) 降至 O(1) 的时间复杂度，总时间复杂度就能从 O(n^2) 降至 O(n)。

<fig1,fig2,fig3,fig4,fig5,fig6,fig7,fig8,fig9>

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int maxScoreSightseeingPair(vector<int>& values) {
        int ans = 0, mx = values[0] + 0;
        for (int j = 1; j < values.size(); ++j) {
            ans = max(ans, mx + values[j] - j);
            // 边遍历边维护
            mx = max(mx, values[j] + j);
        }
        return ans;
    }
};
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public int maxScoreSightseeingPair(int[] values) {
        int ans = 0, mx = values[0] + 0;
        for (int j = 1; j < values.length; ++j) {
            ans = Math.max(ans, mx + values[j] - j);
            // 边遍历边维护
            mx = Math.max(mx, values[j] + j);
        }
        return ans;
    }
}
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
func maxScoreSightseeingPair(values []int) int {
    ans, mx := 0, values[0] + 0
    for j := 1; j < len(values); j++ {
        ans = max(ans, mx + values[j] - j)
        // 边遍历边维护
        mx = max(mx, values[j] + j)
    }
    return ans
}

func max(x, y int) int {
    if x > y {
        return x
    }
    return y
}
[sol1-C#]
1
2
3
4
5
6
7
8
9
10
11
public class Solution {
    public int MaxScoreSightseeingPair(int[] values) {
        int ans = 0, mx = values[0] + 0;
        for (int j = 1; j < values.Length; ++j) {
            ans = Math.Max(ans, mx + values[j] - j);
            // 边遍历边维护
            mx = Math.Max(mx, values[j] + j);
        }
        return ans;
    }
}

复杂度分析

  • 时间复杂度：O(n)，其中 n 为数组 values 的大小。我们只需要遍历一遍数组即可。

  • 空间复杂度：O(1)。我们只需要常数空间来存放若干变量。

 Comments
On this page
1014-最佳观光组合