1026-节点与其祖先之间的最大差值

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:32 2023-09-13 16:06:32 Updated    

给定二叉树的根节点 root，找出存在于 不同 节点 A 和 B 之间的最大值 V，其中 V = |A.val - B.val|，且 A 是 B 的祖先。

（如果 A 的任何子节点之一为 B，或者 A 的任何子节点是 B 的祖先，那么我们认为 A 是 B 的祖先）

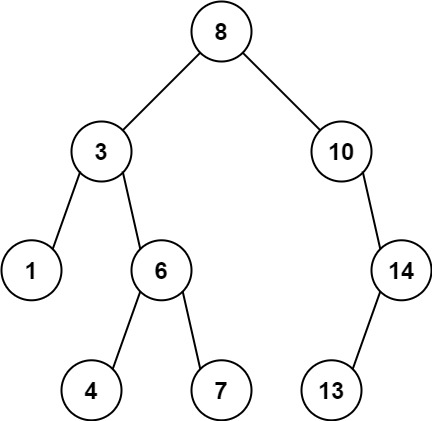
示例 1：

**输入：** root = [8,3,10,1,6,null,14,null,null,4,7,13]
**输出：** 7
**解释：**
我们有大量的节点与其祖先的差值，其中一些如下：
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
在所有可能的差值中，最大值 7 由 |8 - 1| = 7 得出。

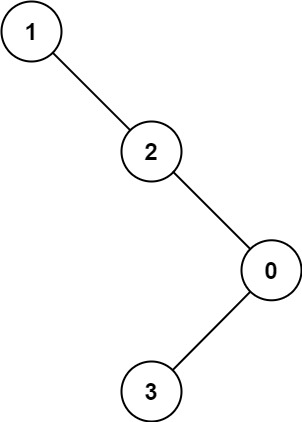
示例 2：

**输入：** root = [1,null,2,null,0,3]
**输出：** 3

提示：

  • 树中的节点数在 2 到 5000 之间。
  • 0 <= Node.val <= 105

方法一：深度优先搜索

题目要求找出所有祖先节点与它的子孙节点的绝对差值的最大值。按照枚举的思路，我们可以枚举子孙节点，然后找出它的所有祖先节点，计算绝对差值。同样地，我们也可以枚举祖先节点，然后找出它的所有子孙节点，计算绝对差值。

以第一种思路为例，并非所有祖先节点都需要被考虑到，我们只需要获取最小的祖先节点以及最大的祖先节点。我们对二叉树执行深度优先搜索，并且记录搜索路径上的节点的最小值 mi 与最大值 ma。假设当前搜索的节点值为 val，那么与该子孙节点与它的所有祖先节点的绝对差值最大值为 \max(|\textit{val} - \textit{mi}|, |\textit{val} - \textit{ma}|)，搜索该节点的左子树与右子树时，对应的 mi} = \min(\textit{mi},\textit{val})，ma} = \max(\textit{ma}, \textit{val})。

  • 为什么只需要获取最小的祖先节点以及最大的祖先节点？

    假设某一子孙节点为 x，对应的最小的祖先节点为 mi，最大的祖先节点为 ma。有任一祖先节点为 y，显然 mi} \le y \le \textit{ma。如果 x \le y，那么 |x - y| = y - x \le \textit{ma} - x = |x - \textit{ma}|，如果 x \gt y，那么 |x - y| = x - y \le x - \textit{mi} = |x - \textit{mi}|，因此最大的绝对差值与祖先节点 y 无关。

  • 第二种思路是否可行？

    可行，需要返回当前子树的最小值和最大值，方法类似。

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int dfs(TreeNode *root, int mi, int ma) {
        if (root == nullptr) {
            return 0;
        }
        int diff = max(abs(root->val - mi), abs(root->val - ma));
        mi = min(mi, root->val);
        ma = max(ma, root->val);
        diff = max(diff, dfs(root->left, mi, ma));
        diff = max(diff, dfs(root->right, mi, ma));
        return diff;
    }

    int maxAncestorDiff(TreeNode* root) {
        return dfs(root, root->val, root->val);
    }
};
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int maxAncestorDiff(TreeNode root) {
        return dfs(root, root.val, root.val);
    }

    public int dfs(TreeNode root, int mi, int ma) {
        if (root == null) {
            return 0;
        }
        int diff = Math.max(Math.abs(root.val - mi), Math.abs(root.val - ma));
        mi = Math.min(mi, root.val);
        ma = Math.max(ma, root.val);
        diff = Math.max(diff, dfs(root.left, mi, ma));
        diff = Math.max(diff, dfs(root.right, mi, ma));
        return diff;
    }
}
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
    def maxAncestorDiff(self, root: Optional[TreeNode]) -> int:
        def dfs(root, mi, ma):
            if root == None:
                return 0
            diff = max(abs(root.val - mi), abs(root.val - ma))
            mi = min(mi, root.val)
            ma = max(ma, root.val)
            diff = max(diff, dfs(root.left, mi, ma))
            diff = max(diff, dfs(root.right, mi, ma))
            return diff
        return dfs(root, root.val, root.val)

[sol1-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
var maxAncestorDiff = function(root) {
    return dfs(root, root.val, root.val);
};

function dfs(root, mi, ma) {
    if (root === null) {
        return 0;
    }
    var diff = Math.max(Math.abs(root.val - mi), Math.abs(root.val - ma));
    mi = Math.min(mi, root.val);
    ma = Math.max(ma, root.val);
    diff = Math.max(diff, dfs(root.left, mi, ma));
    diff = Math.max(diff, dfs(root.right, mi, ma));
    return diff;
}
[sol1-C#]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public class Solution {
    public int MaxAncestorDiff(TreeNode root) {
        return DFS(root, root.val, root.val);
    }

    public int DFS(TreeNode root, int mi, int ma) {
        if (root == null) {
            return 0;
        }
        int diff = Math.Max(Math.Abs(root.val - mi), Math.Abs(root.val - ma));
        mi = Math.Min(mi, root.val);
        ma = Math.Max(ma, root.val);
        diff = Math.Max(diff, DFS(root.left, mi, ma));
        diff = Math.Max(diff, DFS(root.right, mi, ma));
        return diff;
    }
}
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

func min(a, b int) int {
    if a < b {
        return a
    }
    return b
}

func abs(a int) int {
    if a < 0 {
        return -a
    }
    return a
}

func dfs(root *TreeNode, mi, ma int) int {
    if root == nil {
        return 0
    }
    diff := max(abs(root.Val - mi), abs(root.Val - ma))
    mi, ma = min(mi, root.Val), max(ma, root.Val)
    diff = max(diff, dfs(root.Left, mi, ma))
    diff = max(diff, dfs(root.Right, mi, ma))
    return diff
}

func maxAncestorDiff(root *TreeNode) int {
    return dfs(root, root.Val, root.Val)
}
[sol1-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
static int max(int a, int b) {
    return a > b ? a : b;
}

static int min(int a, int b) {
    return a < b ? a : b;
}

int dfs(struct TreeNode *root, int mi, int ma) {
    if (root == NULL) {
        return 0;
    }
    int diff = max(abs(root->val - mi), abs(root->val - ma));
    mi = min(mi, root->val);
    ma = max(ma, root->val);
    diff = max(diff, dfs(root->left, mi, ma));
    diff = max(diff, dfs(root->right, mi, ma));
    return diff;
}

int maxAncestorDiff(struct TreeNode* root){
    return dfs(root, root->val, root->val);
}

复杂度分析

  • 时间复杂度：O(n)，其中 n 是二叉树的节点数目。遍历二叉树的所有节点需要 O(n)。

  • 空间复杂度：O(n)。最坏情况下，二叉树退化为链表，递归栈的空间为 O(n)。

 Comments
On this page
1026-节点与其祖先之间的最大差值