1028-从先序遍历还原二叉树

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:27 2023-09-13 16:06:27 Updated    

我们从二叉树的根节点 root 开始进行深度优先搜索。

在遍历中的每个节点处，我们输出 D 条短划线（其中 D 是该节点的深度），然后输出该节点的值。（ 如果节点的深度为D，则其直接子节点的深度为
D + 1。根节点的深度为 0）。

如果节点只有一个子节点，那么保证该子节点为左子节点。

给出遍历输出 S，还原树并返回其根节点 root。

示例 1：

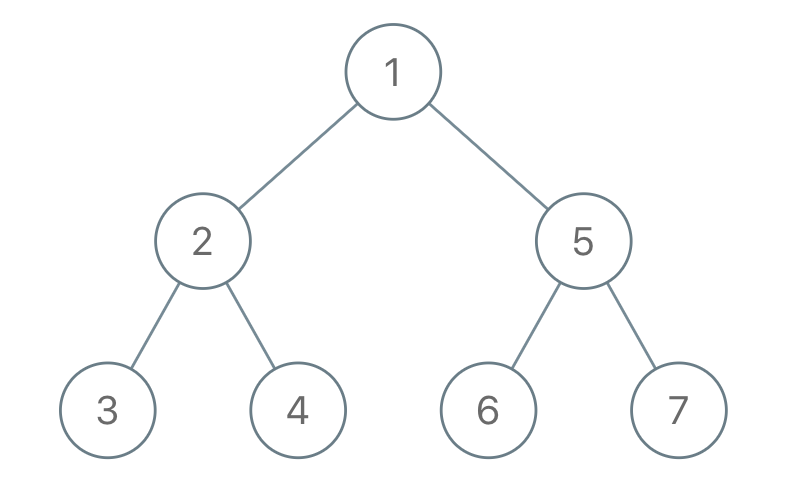
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2019/04/12/recover-a-tree-from-preorder-traversal.png)

**输入：** "1-2--3--4-5--6--7"
**输出：** [1,2,5,3,4,6,7]

示例 2：

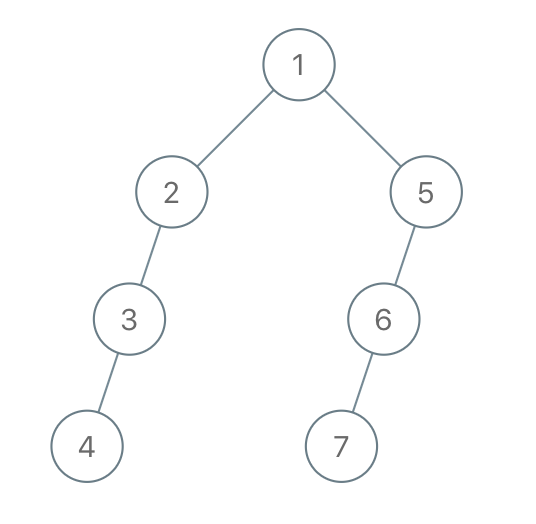
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2019/04/12/screen-shot-2019-04-10-at-114101-pm.png)

**输入：** "1-2--3---4-5--6---7"
**输出：** [1,2,5,3,null,6,null,4,null,7]

示例 3：

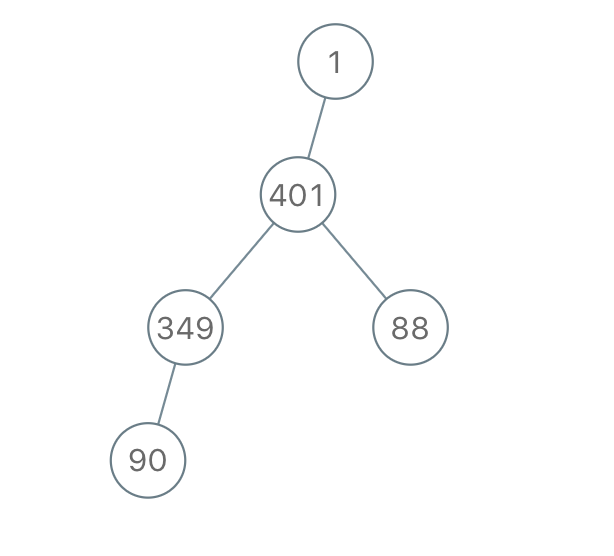
![](https://assets.leetcode-cn.com/aliyun-lc-upload/uploads/2019/04/12/screen-
shot-2019-04-10-at-114955-pm.png)

**输入：** "1-401--349---90--88"
**输出：** [1,401,null,349,88,90]

提示：

  • 原始树中的节点数介于 1 和 1000 之间。
  • 每个节点的值介于 1 和 10 ^ 9 之间。

前言

相较于传统的递归 + 回溯的实现方法而言，本题使用迭代方法（模拟递归）更加简洁方便。

方法一：迭代

我们每次从字符串 s 中取出一个节点的值以及它的深度信息。具体地：

  • 我们首先读取若干个字符 -，直到遇到非 - 字符位置。通过 - 的个数，我们就可以知道当前节点的深度信息；

  • 我们再读取若干个数字，直到遇到非数字或者字符串的结尾。通过这些数字，我们就可以知道当前节点的值。

得到这些信息之后，我们就需要考虑将当前的节点放在何处。记当前节点为 T，上一个节点为 S，那么实际上只有两种情况：

  • T 是 S 的左子节点；

  • T 是根节点到 S 这一条路径上（不包括 S）某一个节点的右子节点。

    • 为什么不包括 S？因为题目中规定了如果节点只有一个子节点，那么保证该子节点为左子节点。在 T 出现之前，S 仍然还是一个叶节点，没有左子节点，因此 T 如果是 S 的子节点，一定是优先变成 S 的左子节点。

这是因为先序遍历本身的性质。在先序遍历中，我们是通过「根 — 左 — 右」的顺序访问每一个节点的。想一想先序遍历的递归 + 回溯方法，对于在先序遍历中任意的两个相邻的节点 S 和 T，要么 T 就是 S 的左子节点（对应上面的第一种情况），要么在遍历到 S 之后发现 S 是个叶节点，于是回溯到之前的某个节点，并开始递归地遍历其右子节点（对应上面的第二种情况）。这样以来，我们按照顺序维护从根节点到当前节点的路径上的所有节点，就可以方便地处理这两种情况。仔细想一想，这实际上就是使用递归 + 回溯的方法遍历一棵树时，栈中的所有节点，也就是可以回溯到的节点。因此我们只需要使用一个栈来模拟递归 + 回溯即可。

回到上面的分析，当我们得到当前节点的值以及深度信息之后，我们可以发现：如果 T 是 S 的左子节点，那么 T 的深度恰好比 S 的深度大 1；在其它的情况下，T 是栈中某个节点（不包括 S）的右子节点，那么我们将栈顶的节点不断地出栈，直到 T 的深度恰好比栈顶节点的深度大 1，此时我们就找到了 T 的双亲节点。

扩展与思考

通过上面的分析，我们只需要借助一个栈，通过迭代的方法就可以还原出这棵二叉树。由于题目给出的 traversal 一定是某棵二叉树的先序遍历结果，因此我们在代码中不需要处理任何异常异常情况。

读者可以进行如下的思考：如果给定的 traversal 只保证由数字和 - 组成，那么我们如何修改代码，使其判断是否能够还原出一棵二叉树呢？

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
public:
    TreeNode* recoverFromPreorder(string traversal) {
        stack<TreeNode*> path;
        int pos = 0;
        while (pos < traversal.size()) {
            int level = 0;
            while (traversal[pos] == '-') {
                ++level;
                ++pos;
            }
            int value = 0;
            while (pos < traversal.size() && isdigit(traversal[pos])) {
                value = value * 10 + (traversal[pos] - '0');
                ++pos;
            }
            TreeNode* node = new TreeNode(value);
            if (level == path.size()) {
                if (!path.empty()) {
                    path.top()->left = node;
                }
            }
            else {
                while (level != path.size()) {
                    path.pop();
                }
                path.top()->right = node;
            }
            path.push(node);
        }
        while (path.size() > 1) {
            path.pop();
        }
        return path.top();
    }
};
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
    public TreeNode recoverFromPreorder(String traversal) {
        Deque<TreeNode> path = new LinkedList<TreeNode>();
        int pos = 0;
        while (pos < traversal.length()) {
            int level = 0;
            while (traversal.charAt(pos) == '-') {
                ++level;
                ++pos;
            }
            int value = 0;
            while (pos < traversal.length() && Character.isDigit(traversal.charAt(pos))) {
                value = value * 10 + (traversal.charAt(pos) - '0');
                ++pos;
            }
            TreeNode node = new TreeNode(value);
            if (level == path.size()) {
                if (!path.isEmpty()) {
                    path.peek().left = node;
                }
            } else {
                while (level != path.size()) {
                    path.pop();
                }
                path.peek().right = node;
            }
            path.push(node);
        }
        while (path.size() > 1) {
            path.pop();
        }
        return path.peek();
    }
}
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution:
    def recoverFromPreorder(self, traversal: str) -> TreeNode:
        path, pos = list(), 0
        while pos < len(traversal):
            level = 0
            while traversal[pos] == '-':
                level += 1
                pos += 1
            value = 0
            while pos < len(traversal) and traversal[pos].isdigit():
                value = value * 10 + (ord(traversal[pos]) - ord('0'))
                pos += 1
            node = TreeNode(value)
            if level == len(path):
                if path:
                    path[-1].left = node
            else:
                path = path[:level]
                path[-1].right = node
            path.append(node)
        return path[0]
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
func recoverFromPreorder(traversal string) *TreeNode {
    path, pos := []*TreeNode{}, 0
    for pos < len(traversal) {
        level := 0
        for traversal[pos] == '-' {
            level++
            pos++
        }
        value := 0
        for ; pos < len(traversal) && traversal[pos] >= '0' && traversal[pos] <= '9'; pos++ {
            value = value * 10 + int(traversal[pos] - '0')
        }
        node := &TreeNode{Val: value}
        if level == len(path) {
            if len(path) > 0 { path[len(path)-1].Left = node }
        } else {
            path = path[:level]
            path[len(path)-1].Right = node
        }
        path = append(path, node)
    }
    return path[0]
}

复杂度分析

  • 时间复杂度：O(|\textit{traversal}|)，其中 |\textit{traversal}| 是字符串 traversal 的长度。我们的算法不断地从 traversal 中取出一个节点的信息，直到取完为止。在这个过程中，我们实际上是对 traversal 进行了一次遍历。

  • 空间复杂度：O(h)，其中 h 是还原出的二叉树的高度。除了作为答案返回的二叉树使用的空间以外，我们使用了一个栈帮助我们进行迭代。由于栈中存放了从根节点到当前节点这一路径上的所有节点，因此最多只会同时有 h 个节点。

 Comments
On this page
1028-从先序遍历还原二叉树