1030-距离顺序排列矩阵单元格

给定四个整数 rows , cols , rCenter 和 cCenter 。有一个 rows x cols
的矩阵，你在单元格上的坐标是 (rCenter, cCenter) 。

返回矩阵中的所有单元格的坐标，并按与 _ _(rCenter, cCenter) _ _ 的 距离 从最小到最大的顺序排。你可以按 任何
满足此条件的顺序返回答案。

单元格(r1, c1) 和 (r2, c2) 之间的距离为|r1 - r2| + |c1 - c2|。

示例 1：

**输入：** rows = 1, cols = 2, rCenter = 0, cCenter = 0
**输出：** [[0,0],[0,1]]
**解释** ：从 (r0, c0) 到其他单元格的距离为：[0,1]

示例 2：

**输入：** rows = 2, cols = 2, rCenter = 0, cCenter = 1
**输出：** [[0,1],[0,0],[1,1],[1,0]]
**解释** ：从 (r0, c0) 到其他单元格的距离为：[0,1,1,2]
[[0,1],[1,1],[0,0],[1,0]] 也会被视作正确答案。

示例 3：

**输入：** rows = 2, cols = 3, rCenter = 1, cCenter = 2
**输出：** [[1,2],[0,2],[1,1],[0,1],[1,0],[0,0]]
**解释** ：从 (r0, c0) 到其他单元格的距离为：[0,1,1,2,2,3]
其他满足题目要求的答案也会被视为正确，例如 [[1,2],[1,1],[0,2],[1,0],[0,1],[0,0]]。

提示：

• 1 <= rows, cols <= 100
• 0 <= rCenter < rows
• 0 <= cCenter < cols

方法一：直接排序

思路及解法

最容易想到的方法是首先存储矩阵内所有的点，然后将其按照哈曼顿距离直接排序。

代码

[sol1-C++]

class Solution {
public:
    vector<vector<int>> allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {
        vector<vector<int>> ret;
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                ret.push_back({i, j});
            }
        }
        sort(ret.begin(), ret.end(), [=](vector<int>& a, vector<int>& b) {
            return abs(a[0] - rCenter) + abs(a[1] - cCenter) < abs(b[0] - rCenter) + abs(b[1] - cCenter);
        });
        return ret;
    }
};

[sol1-Java]

class Solution {
    public int[][] allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {
        int[][] ret = new int[rows * cols][];
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                ret[i * cols + j] = new int[]{i, j};
            }
        }
        Arrays.sort(ret, new Comparator<int[]>() {
            public int compare(int[] a, int[] b) {
                return (Math.abs(a[0] - rCenter) + Math.abs(a[1] - cCenter)) - (Math.abs(b[0] - rCenter) + Math.abs(b[1] - cCenter));
            }
        });
        return ret;
    }
}

[sol1-Golang]

func allCellsDistOrder(rows, cols, rCenter, cCenter int) [][]int {
    ans := make([][]int, 0, rows*cols)
    for i := 0; i < rows; i++ {
        for j := 0; j < cols; j++ {
            ans = append(ans, []int{i, j})
        }
    }
    sort.Slice(ans, func(i, j int) bool {
        a, b := ans[i], ans[j]
        return abs(a[0]-rCenter)+abs(a[1]-cCenter) < abs(b[0]-rCenter)+abs(b[1]-cCenter)
    })
    return ans
}

func abs(x int) int {
    if x < 0 {
        return -x
    }
    return x
}

[sol1-Python3]

class Solution:
    def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:
        ret = [(i, j) for i in range(rows) for j in range(cols)]
        ret.sort(key=lambda x: abs(x[0] - rCenter) + abs(x[1] - cCenter))
        return ret

[sol1-C]

int r0, c0;

int cmp(void* _a, void* _b) {
    int *a = *(int**)_a, *b = *(int**)_b;
    return fabs(a[0] - r0) + fabs(a[1] - c0) - fabs(b[0] - r0) - fabs(b[1] - c0);
}

int** allCellsDistOrder(int rows, int cols, int rCenter, int cCenter, int* returnSize, int** returnColumnSizes) {
    r0 = rCenter, c0 = cCenter;
    int** ret = malloc(sizeof(int*) * rows * cols);
    *returnColumnSizes = malloc(sizeof(int) * rows * cols);
    for (int i = 0; i < rows * cols; i++) {
        (*returnColumnSizes)[i] = 2;
        ret[i] = malloc(sizeof(int) * 2);
    }
    *returnSize = 0;
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < cols; j++) {
            ret[*returnSize][0] = i;
            ret[*returnSize][1] = j;
            (*returnSize)++;
        }
    }
    qsort(ret, rows * cols, sizeof(int*), cmp);
    return ret;
}

复杂度分析

• 时间复杂度：O(\textit{rows} \times \textit{cols} \times \log(\textit{rows} \times \textit{cols}))，存储所有点时间复杂度 O(\textit{rows} \times \textit{cols})，排序时间复杂度 O(\textit{rows} \times \textit{cols} \log(\textit{rows} \times \textit{cols}))。

• 空间复杂度：O(\log(\textit{rows} \times \textit{cols}))，即为排序需要使用的栈空间，不考虑返回值的空间占用。

方法二：桶排序

思路及解法

注意到方法一中排序的时间复杂度太高。实际在枚举所有点时，我们可以直接按照哈曼顿距离分桶。这样我们就可以实现线性的桶排序。

代码

[sol2-C++]

class Solution {
public:
    int dist(int r1, int c1, int r2, int c2) {
        return abs(r1 - r2) + abs(c1 - c2);
    }

    vector<vector<int>> allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {
        int maxDist = max(rCenter, rows - 1 - rCenter) + max(cCenter, cols - 1 - cCenter);
        vector<vector<vector<int>>> bucket(maxDist + 1);

        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                int d = dist(i, j, rCenter, cCenter);
                vector<int> tmp = {i, j};
                bucket[d].push_back(move(tmp));
            }
        }
        vector<vector<int>> ret;
        for (int i = 0; i <= maxDist; i++) {
            for (auto &it : bucket[i]) {
                ret.push_back(it);
            }
        }
        return ret;
    }
};

[sol2-Java]

class Solution {
    public int[][] allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {
        int maxDist = Math.max(rCenter, rows - 1 - rCenter) + Math.max(cCenter, cols - 1 - cCenter);
        List<List<int[]>> bucket = new ArrayList<List<int[]>>();
        for (int i = 0; i <= maxDist; i++) {
            bucket.add(new ArrayList<int[]>());
        }

        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                int d = dist(i, j, rCenter, cCenter);
                bucket.get(d).add(new int[]{i, j});
            }
        }
        int[][] ret = new int[rows * cols][];
        int index = 0;
        for (int i = 0; i <= maxDist; i++) {
            for (int[] it : bucket.get(i)) {
                ret[index++] = it;
            }
        }
        return ret;
    }

    public int dist(int r1, int c1, int r2, int c2) {
        return Math.abs(r1 - r2) + Math.abs(c1 - c2);
    }
}

[sol2-Golang]

func allCellsDistOrder(rows, cols, rCenter, cCenter int) [][]int {
    maxDist := max(rCenter, rows-1-rCenter) + max(cCenter, cols-1-cCenter)
    buckets := make([][][]int, maxDist+1)

    for i := 0; i < rows; i++ {
        for j := 0; j < cols; j++ {
            dist := abs(i-rCenter) + abs(j-cCenter)
            buckets[dist] = append(buckets[dist], []int{i, j})
        }
    }

    ans := make([][]int, 0, rows*cols)
    for _, bucket := range buckets {
        ans = append(ans, bucket...)
    }
    return ans
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

func abs(x int) int {
    if x < 0 {
        return -x
    }
    return x
}

[sol2-Python3]

class Solution:
    def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:
        maxDist = max(rCenter, rows - 1 - rCenter) + max(cCenter, cols - 1 - cCenter)
        bucket = collections.defaultdict(list)
        dist = lambda r1, c1, r2, c2: abs(r1 - r2) + abs(c1 - c2)

        for i in range(rows):
            for j in range(cols):
                bucket[dist(i, j, rCenter, cCenter)].append([i, j])

        ret = list()
        for i in range(maxDist + 1):
            ret.extend(bucket[i])
        
        return ret

[sol2-C]

int dist(int r1, int c1, int r2, int c2) {
    return fabs(r1 - r2) + fabs(c1 - c2);
}

int** allCellsDistOrder(int rows, int cols, int rCenter, int cCenter, int* returnSize, int** returnColumnSizes) {
    int maxDist = fmax(rCenter, rows - 1 - rCenter) + fmax(cCenter, cols - 1 - cCenter);
    int* bucket[maxDist + 1][2 * (rows + cols)];
    int bucketSize[maxDist + 1];
    memset(bucketSize, 0, sizeof(bucketSize));
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < cols; j++) {
            int d = dist(i, j, rCenter, cCenter);
            int* tmp = malloc(sizeof(int) * 2);
            tmp[0] = i, tmp[1] = j;
            bucket[d][bucketSize[d]++] = tmp;
        }
    }

    int** ret = malloc(sizeof(int*) * rows * cols);
    *returnColumnSizes = malloc(sizeof(int) * rows * cols);
    for (int i = 0; i < rows * cols; i++) {
        (*returnColumnSizes)[i] = 2;
    }
    *returnSize = 0;
    for (int i = 0; i <= maxDist; i++) {
        for (int j = 0; j < bucketSize[i]; j++) {
            ret[(*returnSize)++] = bucket[i][j];
        }
    }
    return ret;
}

复杂度分析

• 时间复杂度：O(\textit{rows} \times \textit{cols})，存储所有点时间复杂度 O(\textit{rows} \times \textit{cols})，桶排序时间复杂度 O(\textit{rows} \times \textit{cols})。

• 空间复杂度：O(\textit{rows} \times \textit{cols})，需要存储矩阵内所有点。

方法三：几何法

思路及解法

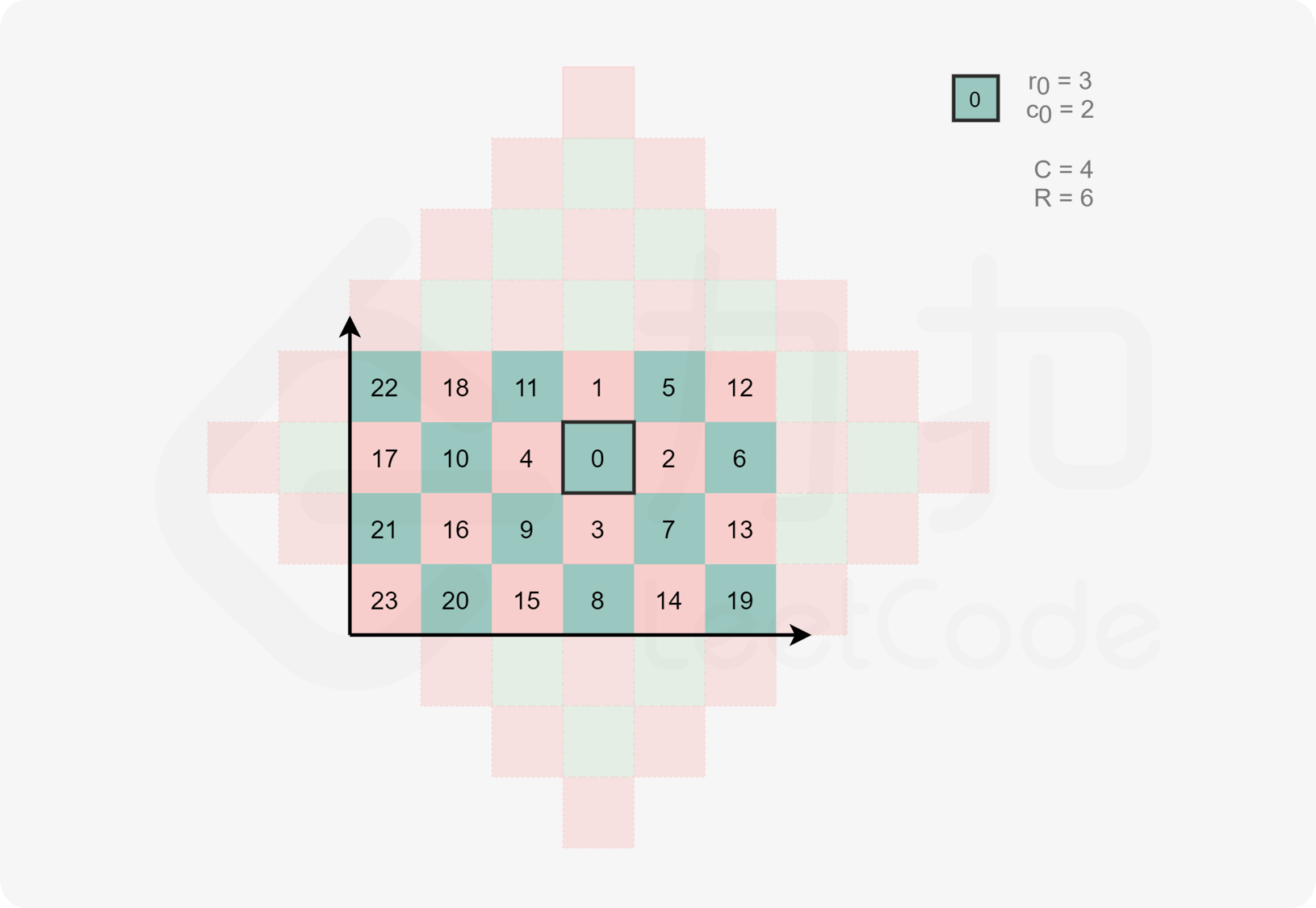
我们也可以直接变换枚举矩阵的顺序，直接按照曼哈顿距离遍历该矩形即可。

注意到曼哈顿距离相同的位置恰好构成一个斜着的正方形边框，因此我们可以从小到大枚举曼哈顿距离，并使用循环来直接枚举该距离对应的边框。我们每次从该正方形边框的上顶点出发，依次经过右顶点、下顶点和左顶点，最后回到上顶点。这样即可完成当前层的遍历。

注意正方形边框中的部分点不一定落在矩阵中，所以我们需要做好边界判断。

代码

[sol3-C++]

class Solution {
public:
    const int dr[4] = {1, 1, -1, -1};
    const int dc[4] = {1, -1, -1, 1};

    vector<vector<int>> allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {
        int maxDist = max(rCenter, rows - 1 - rCenter) + max(cCenter, cols - 1 - cCenter);
        vector<vector<int>> ret;
        int row = rCenter, col = cCenter;
        ret.push_back({row, col});
        for (int dist = 1; dist <= maxDist; dist++) {
            row--;
            for (int i = 0; i < 4; i++) {
                while ((i % 2 == 0 && row != rCenter) || (i % 2 != 0 && col != cCenter)) {
                    if (row >= 0 && row < rows && col >= 0 && col < cols) {
                        ret.push_back({row, col});
                    }
                    row += dr[i];
                    col += dc[i];
                }
            }
        }
        return ret;
    }
};

[sol3-Java]

class Solution {
    int[] dr = {1, 1, -1, -1};
    int[] dc = {1, -1, -1, 1};

    public int[][] allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {
        int maxDist = Math.max(rCenter, rows - 1 - rCenter) + Math.max(cCenter, cols - 1 - cCenter);
        int[][] ret = new int[rows * cols][];
        int row = rCenter, col = cCenter;
        int index = 0;
        ret[index++] = new int[]{row, col};
        for (int dist = 1; dist <= maxDist; dist++) {
            row--;
            for (int i = 0; i < 4; i++) {
                while ((i % 2 == 0 && row != rCenter) || (i % 2 != 0 && col != cCenter)) {
                    if (row >= 0 && row < rows && col >= 0 && col < cols) {
                        ret[index++] = new int[]{row, col};
                    }
                    row += dr[i];
                    col += dc[i];
                }
            }
        }
        return ret;
    }
}

[sol3-Golang]

var dir4 = [][2]int{ {1, 1}, {1, -1}, {-1, -1}, {-1, 1} }

func allCellsDistOrder(rows, cols, rCenter, cCenter int) [][]int {
    ans := make([][]int, 1, rows*cols)
    ans[0] = []int{rCenter, cCenter}
    maxDist := max(rCenter, rows-1-rCenter) + max(cCenter, cols-1-cCenter)
    row, col := rCenter, cCenter
    for dist := 1; dist <= maxDist; dist++ {
        row--
        for i, dir := range dir4 {
            for i%2 == 0 && row != rCenter || i%2 == 1 && col != cCenter {
                if 0 <= row && row < rows && 0 <= col && col < cols {
                    ans = append(ans, []int{row, col})
                }
                row += dir[0]
                col += dir[1]
            }
        }
    }
    return ans
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

[sol3-Python3]

class Solution:
    def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:
        dirs = [(1, 1), (1, -1), (-1, -1), (-1, 1)]
        maxDist = max(rCenter, rows - 1 - rCenter) + max(cCenter, cols - 1 - cCenter)
        row, col = rCenter, cCenter
        ret = [[row, col]]
        for dist in range(1, maxDist + 1):
            row -= 1
            for i, (dr, dc) in enumerate(dirs):
                while (i % 2 == 0 and row != rCenter) or (i % 2 != 0 and col != cCenter):
                    if 0 <= row < rows and 0 <= col < cols:
                        ret.append([row, col])
                    row += dr
                    col += dc
        return ret

[sol3-C]

const int dr[4] = {1, 1, -1, -1};
const int dc[4] = {1, -1, -1, 1};

int** allCellsDistOrder(int rows, int cols, int rCenter, int cCenter, int* returnSize, int** returnColumnSizes) {
    int maxDist = fmax(rCenter, rows - 1 - rCenter) + fmax(cCenter, cols - 1 - cCenter);

    int** ret = malloc(sizeof(int*) * rows * cols);
    *returnColumnSizes = malloc(sizeof(int) * rows * cols);
    for (int i = 0; i < rows * cols; i++) {
        (*returnColumnSizes)[i] = 2;
    }

    int row = rCenter, col = cCenter;
    *returnSize = 0;
    int* tmp = malloc(sizeof(int) * 2);
    tmp[0] = row, tmp[1] = col;
    ret[(*returnSize)++] = tmp;
    for (int dist = 1; dist <= maxDist; dist++) {
        row--;
        for (int i = 0; i < 4; i++) {
            while ((i % 2 == 0 && row != rCenter) || (i % 2 != 0 && col != cCenter)) {
                if (row >= 0 && row < rows && col >= 0 && col < cols) {
                    int* tmps = malloc(sizeof(int) * 2);
                    tmps[0] = row, tmps[1] = col;
                    ret[(*returnSize)++] = tmps;
                }
                row += dr[i];
                col += dc[i];
            }
        }
    }
    return ret;
}

复杂度分析

• 时间复杂度：O\big((\textit{rows}+\textit{cols})^2\big)，我们需要遍历矩阵内所有点，同时也会遍历部分超过矩阵部分的点。在最坏情况下，给定的单元格位于矩阵的一个角，例如 (0,0)，此时最大的曼哈顿距离为 rows}+\textit{cols}-2，需要遍历的点数为 2(\textit{rows}+\textit{cols}-2)(\textit{rows}+\textit{cols}-1)+1，因此时间复杂度为 O\big((\textit{rows}+\textit{cols})^2\big)。

• 空间复杂度：O(1)，不考虑返回值的空间占用。