1039-多边形三角剖分的最低得分
你有一个凸的 n 边形,其每个顶点都有一个整数值。给定一个整数数组 values ,其中 values[i] 是第 i 个顶点的值(即
顺时针顺序 )。
假设将多边形 剖分 为 n - 2 个三角形。对于每个三角形,该三角形的值是顶点标记的 乘积 ,三角剖分的分数是进行三角剖分后所有n - 2 个三角形的值之和。
返回 多边形进行三角剖分后可以得到的最低分 。
示例 1:
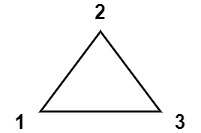
**输入:** values = [1,2,3]
**输出:** 6
**解释:** 多边形已经三角化,唯一三角形的分数为 6。
示例 2:
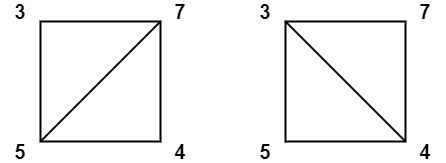
**输入:** values = [3,7,4,5]
**输出:** 144
**解释:** 有两种三角剖分,可能得分分别为:3*7*5 + 4*5*7 = 245,或 3*4*5 + 3*4*7 = 144。最低分数为 144。
示例 3:
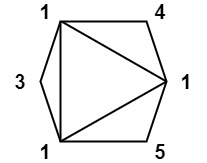
**输入:** values = [1,3,1,4,1,5]
**输出:** 13
**解释:** 最低分数三角剖分的得分情况为 1*1*3 + 1*1*4 + 1*1*5 + 1*1*1 = 13。
提示:
n == values.length3 <= n <= 501 <= values[i] <= 100
方法一:动态规划
思路
设 dp}[i][j](j\geq i+2) 的值为顶点 i, i+1, \dots, j-1, j 构成的凸 j-i+1 边形进行三角形剖分后可以得到的最低分。当 i+2=j 时,凸多边形退化为三角形。其他情况下,需要进行剖分,假设剖分得到的三角形中,顶点 i, j 和另一个顶点 k(i<k<j) 构成了一个三角形,那么三角形 ikj 就将这个凸多边形分成了三部分:
- 顶点 i, i+1, \dots, k-1, k 构成的凸 k-i+1 边形。当 k=i+1 时,这部分不存在。
- 顶点 i, k, j 构成的三角形。
- 顶点 k, k+1, \dots, j-1, j 构成的凸 j-k+1 边形。当 j=k+1 时,这部分不存在。
凸多边形的值就是这三部分的值之和。可以通过遍历 k 的值,来求出多边形的值的最小值。而第一部分和第三部分的值,也可以通过相同的方法求得最小值。
代码实现上,可以通过记忆化搜索来完成。最后返回 dp}[0][n-1] 即可。
代码
1 | class Solution: |
1 | class Solution { |
1 | public class Solution { |
1 | class Solution { |
1 | typedef struct { |
1 | var minScoreTriangulation = function(values) { |
1 | func minScoreTriangulation(values []int) int { |
复杂度分析
时间复杂度:O(n^3)。动态规划一共有 O(n^2) 个状态,计算每个状态消耗 O(n)。
空间复杂度:O(n^2)。动态规划一共有 O(n^2) 个状态。
Comments