1071-字符串的最大公因子

对于字符串 s 和 t，只有在 s = t + ... + t（t 自身连接 1 次或多次）时，我们才认定 “t 能除尽 s”。

给定两个字符串 str1 和 str2 。返回 最长字符串 x，要求满足 x 能除尽 str1 且 x 能除尽 str2
。

示例 1：

**输入：** str1 = "ABCABC", str2 = "ABC"
**输出：** "ABC"

示例 2：

**输入：** str1 = "ABABAB", str2 = "ABAB"
**输出：** "AB"

示例 3：

**输入：** str1 = "LEET", str2 = "CODE"
**输出：** ""

提示：

• 1 <= str1.length, str2.length <= 1000
• str1 和 str2 由大写英文字母组成

预备知识

• 约数，最大公约数
• 辗转相除法

方法一：枚举

思路和算法

首先答案肯定是字符串的某个前缀，然后简单直观的想法就是枚举所有的前缀来判断，我们设这个前缀串长度为 len}_x，str1 的长度为 len}_1，str2 的长度为 len}_2，则我们知道前缀串的长度必然要是两个字符串长度的约数才能满足条件，否则无法经过若干次拼接后得到长度相等的字符串，公式化来说，即

len}_1 \mod \textit{len}_x == 0
len}_2 \mod \textit{len}_x == 0

所以我们可以枚举符合长度条件的前缀串，再去判断这个前缀串拼接若干次以后是否等于 str1 和 str2 即可。

由于题目要求最长的符合要求的字符串 X，所以可以按长度从大到小枚举前缀串，这样碰到第一个满足条件的前缀串返回即可。

[sol1-C++]

class Solution {
    bool check(string t,string s){
        int lenx = (int)s.length() / (int)t.length();
        string ans = "";
        for (int i = 1; i <= lenx; ++i){
            ans = ans + t;
        }
        return ans == s;
    }
public:
    string gcdOfStrings(string str1, string str2) {
        int len1 = (int)str1.length(), len2 = (int)str2.length();
        for (int i = min(len1, len2); i >= 1; --i){ // 从长度大的开始枚举
            if (len1 % i == 0 && len2 % i == 0){
                string X = str1.substr(0, i);
                if (check(X, str1) && check(X, str2)) return X;
            }
        }
        return "";
    }
};

[sol1-Java]

class Solution {
    public String gcdOfStrings(String str1, String str2) {
        int len1 = str1.length(), len2 = str2.length();
        for (int i = Math.min(len1, len2); i >= 1; --i) { // 从长度大的开始枚举
            if (len1 % i == 0 && len2 % i == 0) {
                String X = str1.substring(0, i);
                if (check(X, str1) && check(X, str2)) {
                    return X;
                }
            }
        }
        return "";
    }

    public boolean check(String t, String s) {
        int lenx = s.length() / t.length();
        StringBuffer ans = new StringBuffer();
        for (int i = 1; i <= lenx; ++i) {
            ans.append(t);
        }
        return ans.toString().equals(s);
    }
}

[sol1-Python3]

class Solution:
    def gcdOfStrings(self, str1: str, str2: str) -> str:
        for i in range(min(len(str1), len(str2)), 0, -1):
            if (len(str1) % i) == 0 and (len(str2) % i) == 0:
                if str1[: i] * (len(str1) // i) == str1 and str1[: i] * (len(str2) // i) == str2:
                    return str1[: i]
        return ''

复杂度分析

• 时间复杂度：O((\textit{len}_1+\textit{len}_2)\sigma(gcd(\textit{len}_1,\textit{len}_2)))，其中 \sigma(n) 表示 n 的约数个数，gcd(a,b) 表示 a 和 b 的的最大公约数。我们需要线性的时间来两两比较拼接后的字符串和被比较的串是否相等，而之前提到符合条件的长度 len}_x 一定是 len}_1 和 len}_2 的公约数，所以符合条件的 len}_x 的个数即为 len}_1 和 len}_2 的公约数个数（即最大公约数的约数个数）\sigma(gcd(\textit{len}_1,\textit{len}_2))，最坏情况下所有符合条件的 len}_x 均要被判断一次，再算上之前提及的判断是否符合的时间复杂度，最后时间复杂度即为 O((\textit{len}_1+\textit{len}_2)\sigma(gcd(\textit{len}_1,\textit{len}_2)))。

• 空间复杂度：O(\textit{len}_1+\textit{len}_2)，每次枚举比较的过程中需要创建长度为 len}_1 和 len}_2 的临时字符串变量，所以需要额外 O(\textit{len}_1+\textit{len}_2) 的空间。

方法二：枚举优化

思路

注意到一个性质：如果存在一个符合要求的字符串 X，那么也一定存在一个符合要求的字符串 X'，它的长度为 str1 和 str2 长度的最大公约数。

简单来说，方法一中我们已经知道符合条件的长度出现在 gcd(\textit{len}_1,\textit{len}_2) 的所有约数中，我们假设其中一个满足条件的约数为 len}_x，该长度为 len}_x 的前缀串 X 能经过若干次拼接后得到 str1 和 str2。拿 str1 举例，X 经过 len_1}{len_x 次拼接后得到了 str1，而 X 又能经过 gcd(\textit{len}_1,\textit{len}_2)}{\textit{len}_x 次拼接后得到长度为 gcd(\textit{len}_1,\textit{len}_2) 的前缀串 X’ ，所以我们可以每次取出 gcd(\textit{len}_1,\textit{len}_2)}{\textit{len}_x 个 X 来用 X’ 完成替换，最后 str1 会被替换成 \textit{len}_1}{gcd(\textit{len}_1,\textit{len}_2) 个 X’ ，str2 同理可得。因此如果存在一个符合要求的字符串 X，那么也一定存在一个符合要求的字符串 X’，它的长度为 str1 和 str2 长度的最大公约数。我们只需要判断长度为 gcd(\textit{len}_1,\textit{len}_2) 的前缀串是否满足要求即可。

算法

由上述性质我们可以先用辗转相除法求得两个字符串长度的最大公约数 gcd(\textit{len}_1,\textit{len}_2)，取出该长度的前缀串，判断一下它是否能经过若干次拼接得到 str1 和 str2 即可。

[sol2-C++]

class Solution {
    bool check(string t,string s){
        int lenx = (int)s.length() / (int)t.length();
        string ans = "";
        for (int i = 1; i <= lenx; ++i){
            ans = ans + t;
        }
        return ans == s;
    }
public:
    string gcdOfStrings(string str1, string str2) {
        int len1 = (int)str1.length(), len2 = (int)str2.length();
        string T = str1.substr(0, __gcd(len1,len2)); // __gcd() 为c++自带的求最大公约数的函数
        if (check(T, str1) && check(T, str2)) return T;
        return "";
    }
};

[sol2-Java]

class Solution {
    public String gcdOfStrings(String str1, String str2) {
        int len1 = str1.length(), len2 = str2.length();
        String T = str1.substring(0, gcd(len1, len2));
        if (check(T, str1) && check(T, str2)) {
            return T;
        }
        return "";
    }

    public boolean check(String t, String s) {
        int lenx = s.length() / t.length();
        StringBuffer ans = new StringBuffer();
        for (int i = 1; i <= lenx; ++i) {
            ans.append(t);
        }
        return ans.toString().equals(s);
    }

    public int gcd(int a, int b) {
        int remainder = a % b;
        while (remainder != 0) {
            a = b;
            b = remainder;
            remainder = a % b;
        }
        return b;
    }
}

[sol2-Python3]

class Solution:
    def gcdOfStrings(self, str1: str, str2: str) -> str:
        candidate_len = math.gcd(len(str1), len(str2))
        candidate = str1[: candidate_len]
        if candidate * (len(str1) // candidate_len) == str1 and candidate * (len(str2) // candidate_len) == str2:
            return candidate
        return ''

复杂度分析

• 时间复杂度：O(n)，其中 n 是两个字符串的长度范围，即 len}_1 + \textit{len}_2。判断最大公约数长度的前缀串是否符合条件需要 O(n) 的时间复杂度，求两个字符串长度的最大公约数需要 O(\log n) 的时间复杂度，所以总时间复杂度为 O(n+\log n)=O(n) 。
• 空间复杂度：O(n)，比较的过程中需要创建一个长度创建长度为 O(n) 的临时字符串变量，所以需要额外 O(n) 的空间。

方法三：数学

思路

需要知道一个性质：**如果 str1 和 str2 拼接后等于 str2和 str1 拼接起来的字符串（注意拼接顺序不同），那么一定存在符合条件的字符串 X**。

先证必要性，即如果存在符合条件的字符串 X ，则 str1 和 str2 拼接后等于 str2和 str1 拼接起来的字符串。

如果字符串 X 符合条件，那么 str1=X+X+...+X+X=n*X ，str2=X+X+..+X+X=m*X，n*X 表示 n 个字符串 X 拼接，m*X 同理，则 str1 与 str2 拼接后的字符串即为 (n+m)*X，而 str2 与 str1 拼接后的字符串即为 (m+n)*X，等于 (n+m)*X，所以必要性得证。

再看充分性，简单来说，我们可以如下图一样先将两个拼接后的字符串放在一起。不失一般性，我们假定 str1 的长度大于 str2，

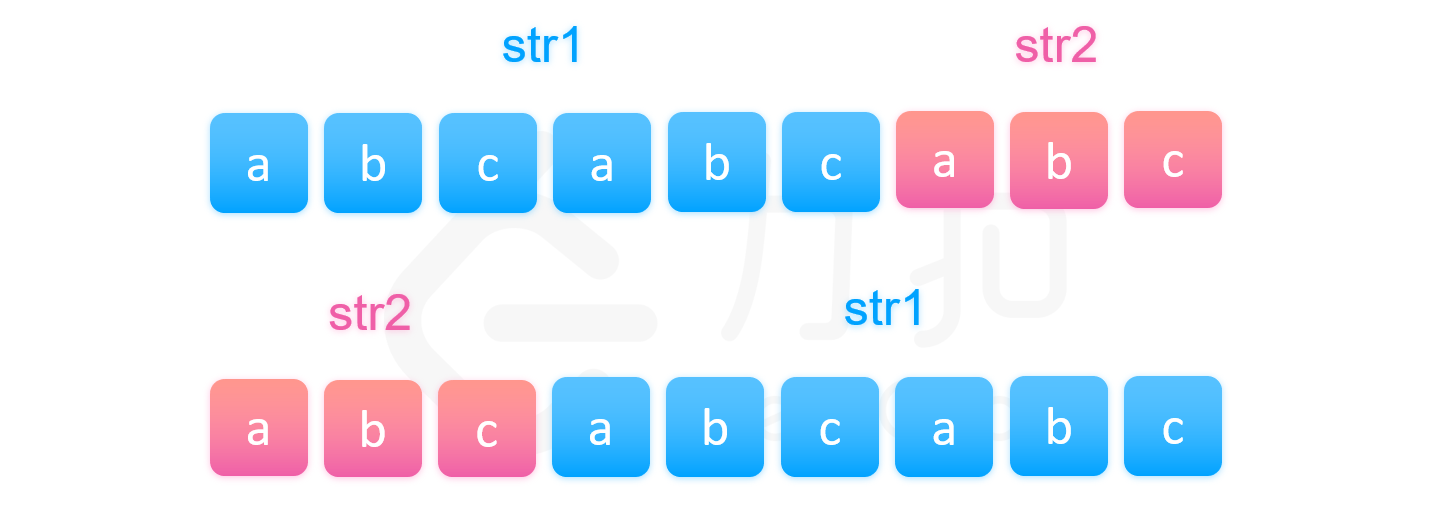
我们等间隔取 gcd(\textit{len}_1,\textit{len}_2) 长度的字符串。

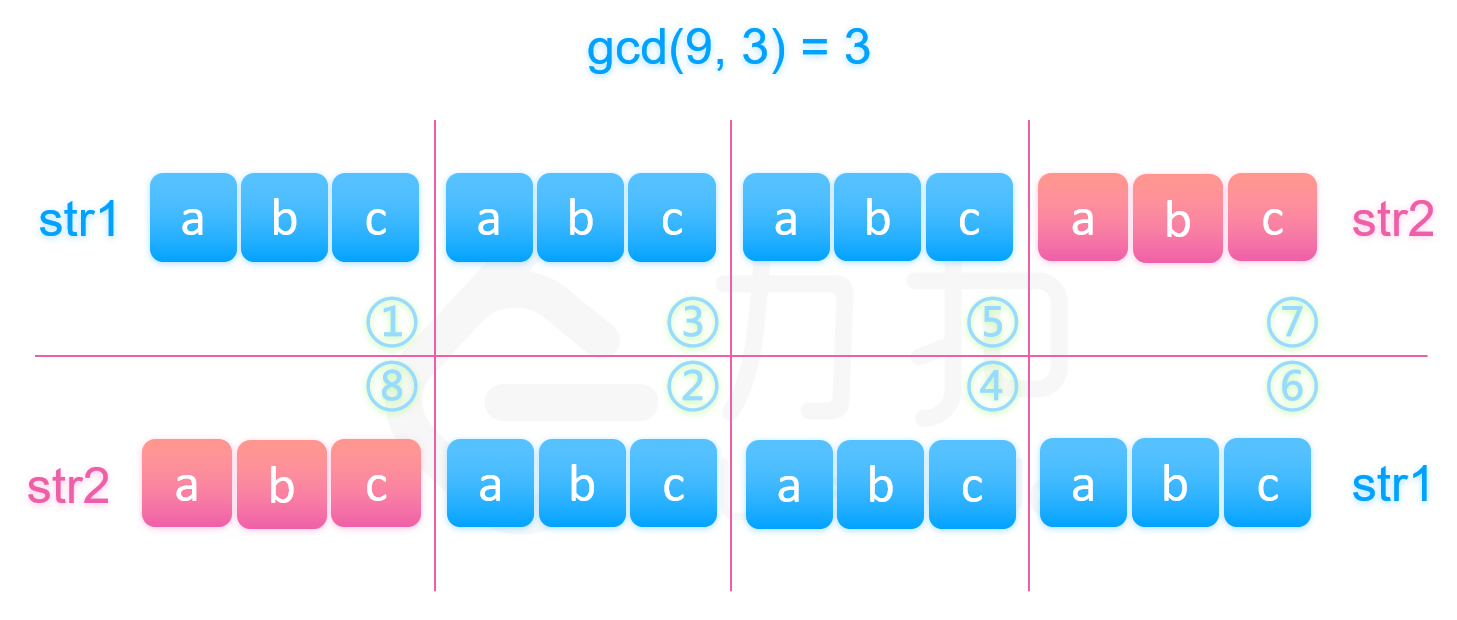
如果该长度等于 str2 的长度，即 str1 的长度可以整除 str2 的长度。我们可以知道，已知图中第一部分等于图中的第二部分（都是字符串 str1 的开头），而图中的第二部分又等于第三部分（两个字符串相等），所以我们知道第三部分也是等于第一部分。同理我们可以推得图中划分的 1,3,5,7 四个部分都相等，所以拼接起来的字符串可以由第一部分的前缀串经过若干次拼接得到。

那么如果不等于 str2 的长度，我们由上文一样的方法可以推得下图中被染颜色相同的字符串片段是相等的，其中每个颜色片段都是长为 gcd(\textit{len}_1,\textit{len}_2) 的字符串。那么不同颜色代表的字符串是否也相等呢？如果相等就可以推得我们的结论是正确的。

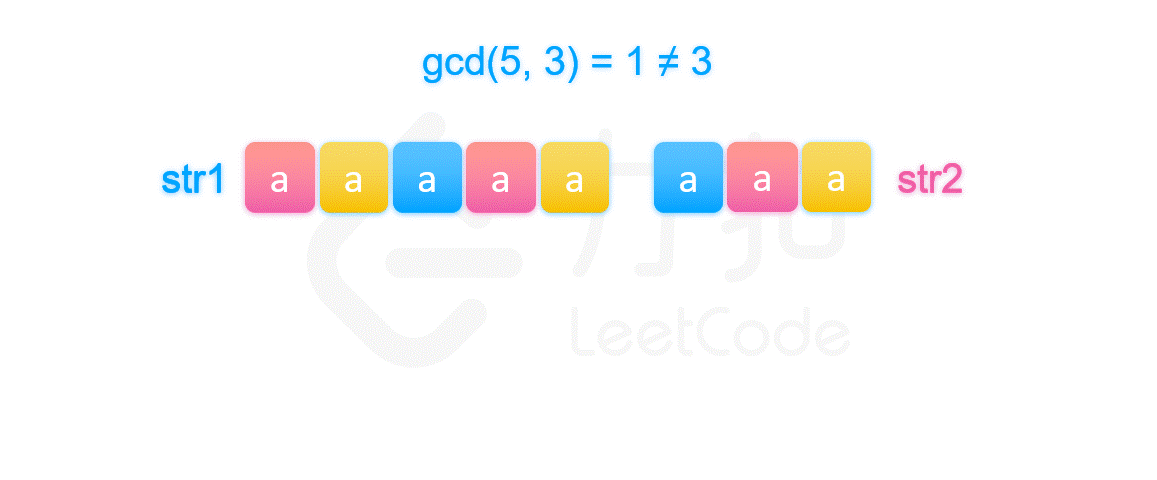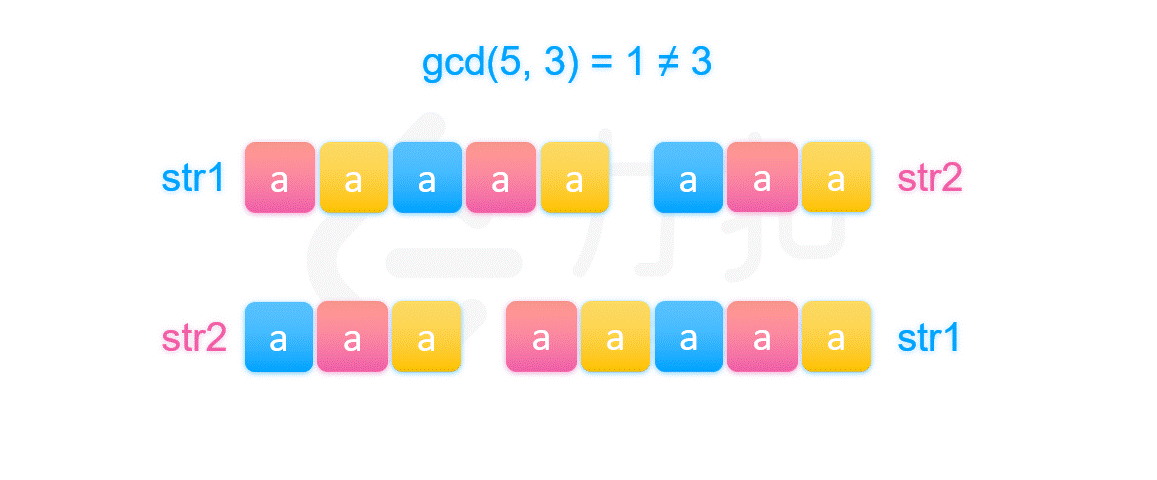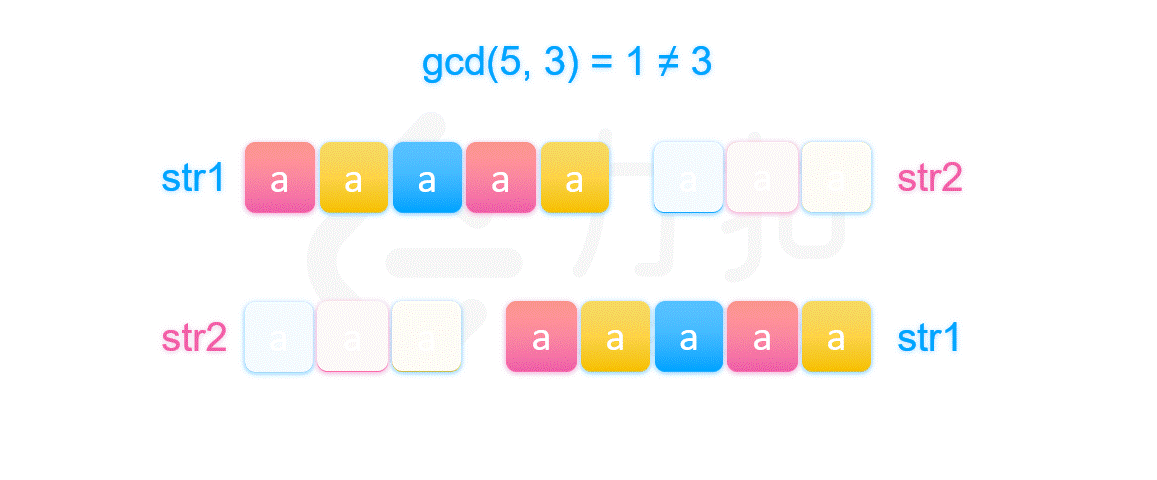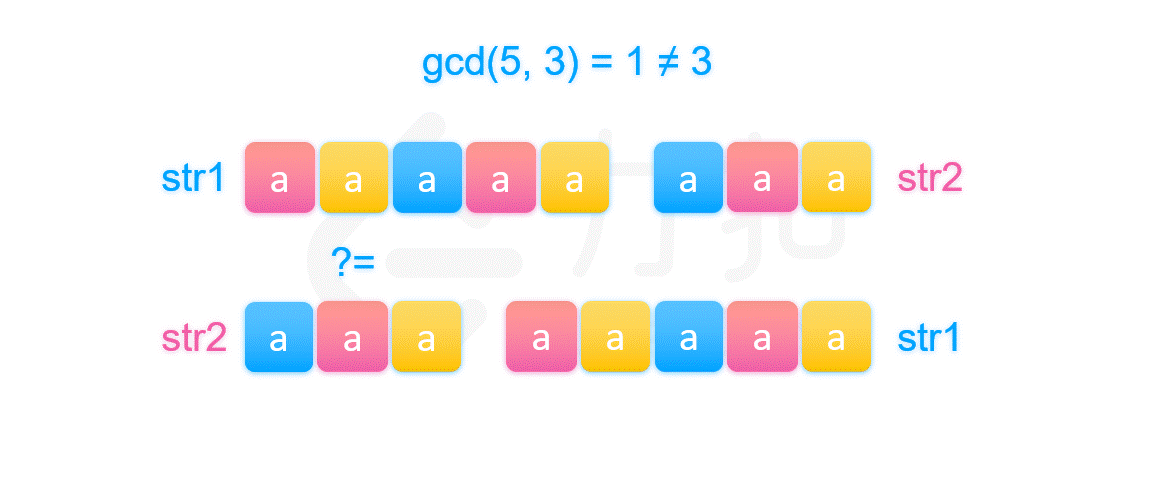
其实由上图我们可以知道，因为第一个字符串和第二个字符串相等，所以两个字符串开头的部分必然相等。我们将前 \textit{len}_2}{gcd(\textit{len}_1,\textit{len}_2) 个被染颜色的部分放在一起比较即可推得不同颜色的部分都是两两相等的，但是这是基于它们开头被染的颜色顺序是不同的，这一定成立吗？

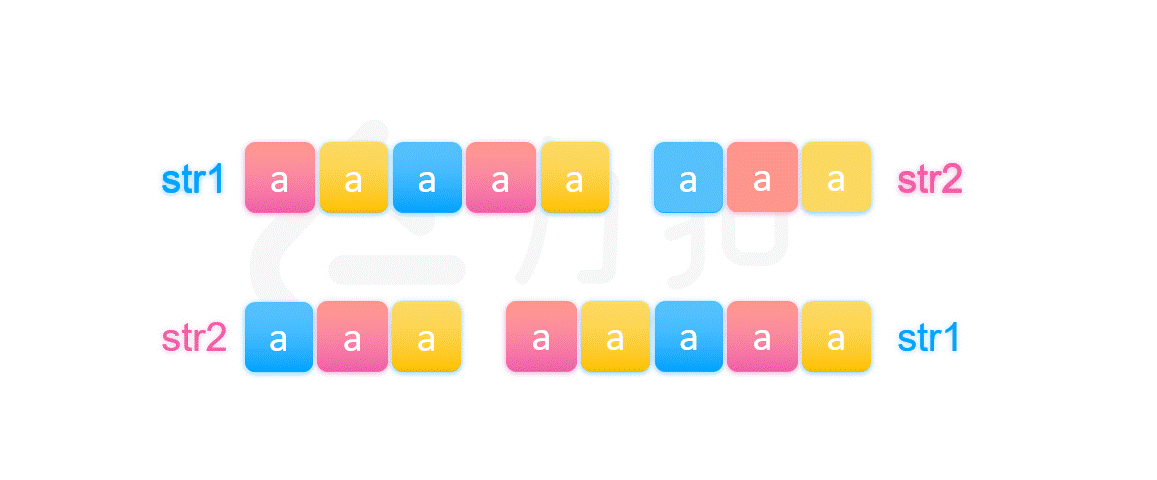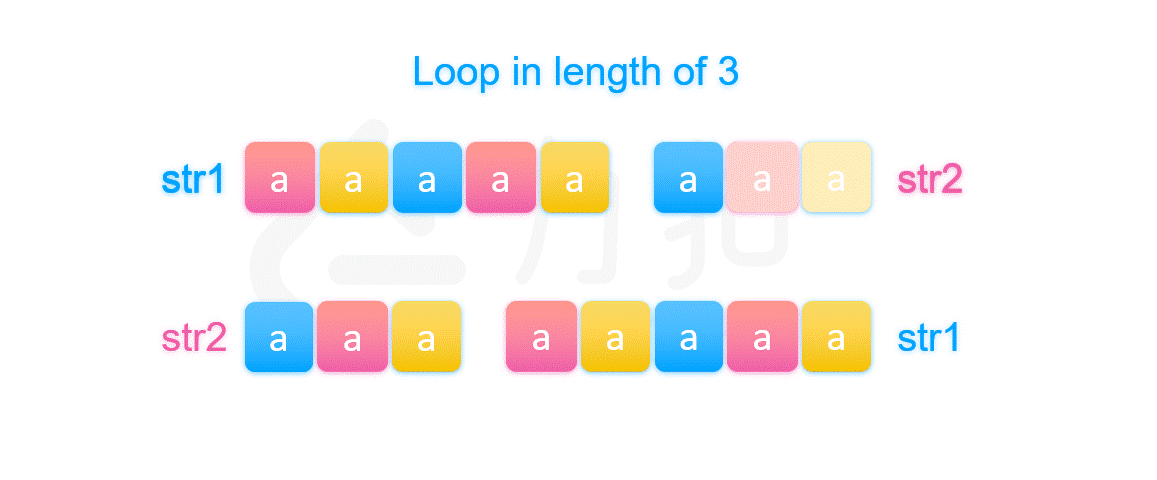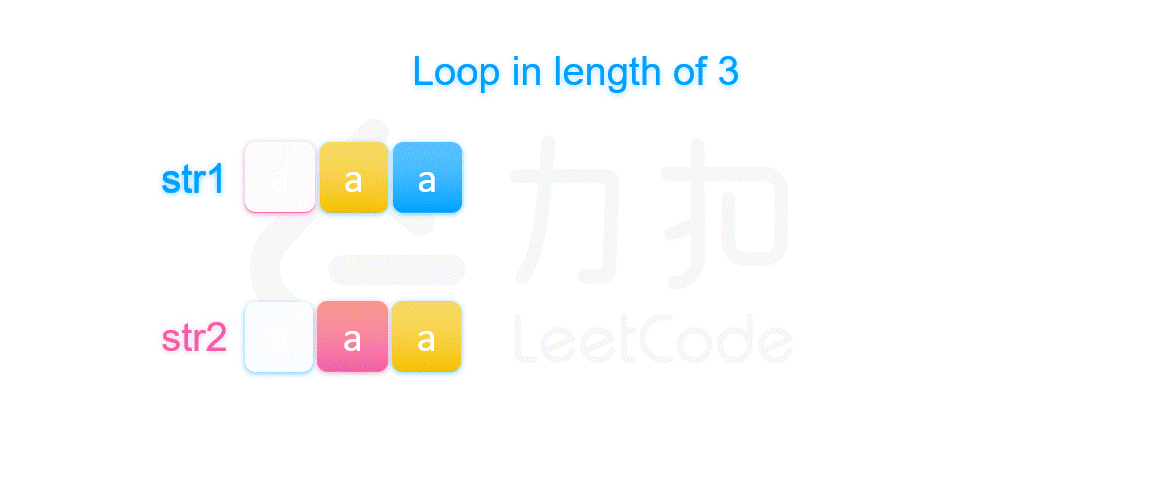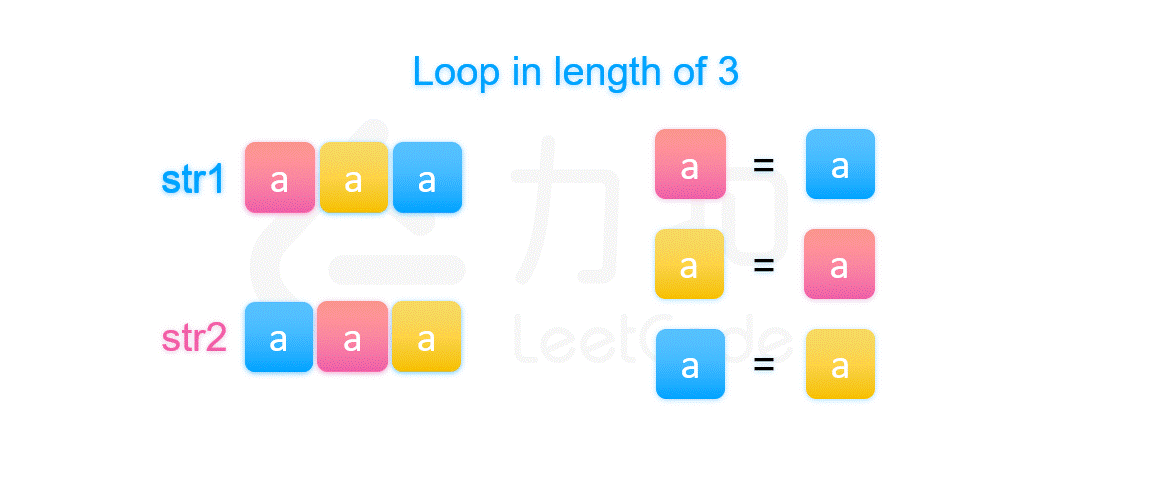
其实图中可以看出第一个字符串被染的颜色是以 str2 的长度在循环的，由于第二种情况下 str1 的长度不整除 str2 的长度，导致第一个字符串的 str1 部分被染完颜色的时候，str2 被染的颜色的顺序必然不等于开头 str1 被染的颜色顺序，而第二个字符串的开头又是 str2，它被染色的顺序是等于第一个字符串中 str2 被染色的顺序的，所以两个字符串的开头被染的颜色顺序一定不同。最后我们就推出如果 str1 和 str2 拼接后等于 str2 和 str1 拼接起来的字符串，那么一定存在符合条件的字符串 X。

算法

有了该性质以及方法二的性质，我们就可以先判断 str1 和 str2 拼接后是否等于 str2 和 str1 拼接起来的字符串，如果等于直接输出长度为 gcd(\textit{len}_1,\textit{len}_2) 的前缀串即可，否则返回空串。

[sol3-C++]

class Solution {
public:
    string gcdOfStrings(string str1, string str2) {
        if (str1 + str2 != str2 + str1) return "";
        return str1.substr(0, __gcd((int)str1.length(), (int)str2.length())); // __gcd() 为c++自带的求最大公约数的函数
    }
};

[sol3-Java]

class Solution {
    public String gcdOfStrings(String str1, String str2) {
        if (!str1.concat(str2).equals(str2.concat(str1))) {
            return "";
        }
        return str1.substring(0, gcd(str1.length(), str2.length()));
    }

    public int gcd(int a, int b) {
        int remainder = a % b;
        while (remainder != 0) {
            a = b;
            b = remainder;
            remainder = a % b;
        }
        return b;
    }
}

[sol3-Python3]

class Solution:
    def gcdOfStrings(self, str1: str, str2: str) -> str:
        candidate_len = math.gcd(len(str1), len(str2))
        candidate = str1[: candidate_len]
        if str1 + str2 == str2 + str1:
            return candidate
        return ''

复杂度分析

• 时间复杂度：O(n) ，字符串拼接比较是否相等需要 O(n) 的时间复杂度，求两个字符串长度的最大公约数需要 O(\log n) 的时间复杂度，所以总时间复杂度为 O(n+\log n)=O(n) 。

• 空间复杂度：O(n) ，程序运行时建立了中间变量用来存储 str1 与 str2 的相加结果。