1091-二进制矩阵中的最短路径

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 17:01:07 2023-09-13 17:01:07 Updated    

给你一个 n x n 的二进制矩阵 grid 中，返回矩阵中最短 畅通路径 的长度。如果不存在这样的路径，返回 -1 。

二进制矩阵中的 畅通路径 是一条从 左上角 单元格（即，(0, 0)）到 右下角 单元格（即，(n - 1, n - 1)）的路径，该路径同时满足下述要求：

  • 路径途经的所有单元格的值都是 0 。
  • 路径中所有相邻的单元格应当在 8 个方向之一 上连通（即，相邻两单元之间彼此不同且共享一条边或者一个角）。

畅通路径的长度 是该路径途经的单元格总数。

示例 1：

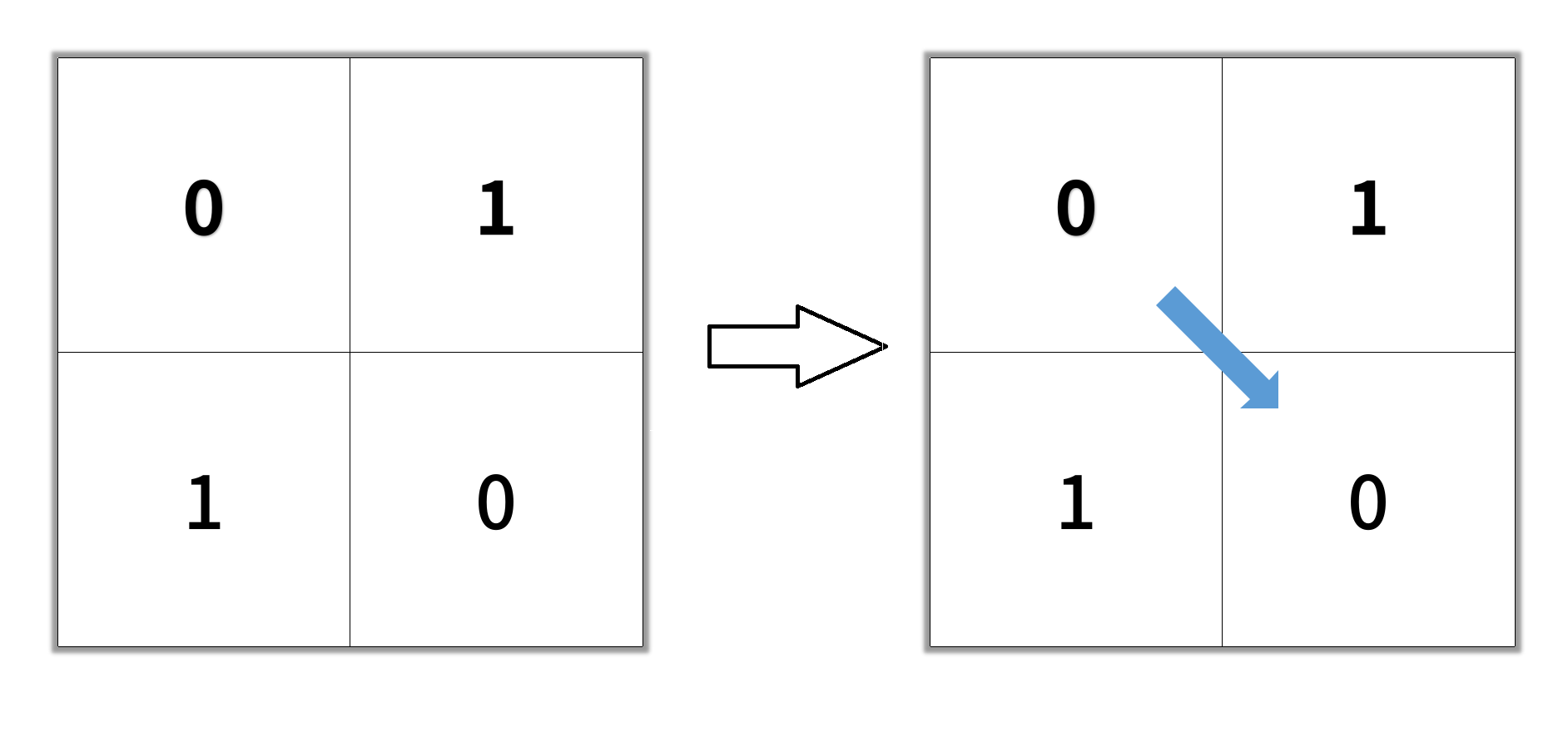
**输入：** grid = [[0,1],[1,0]]
**输出：** 2

示例 2：

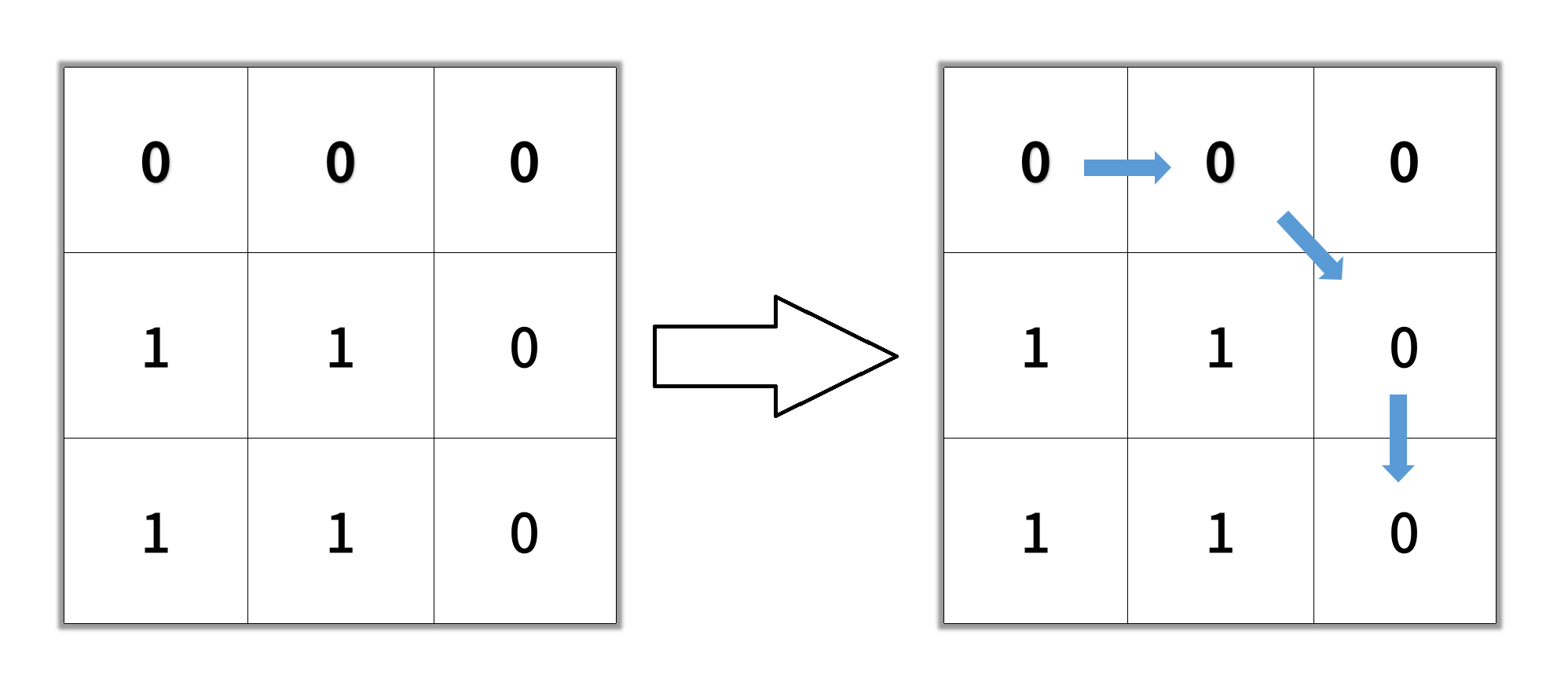
**输入：** grid = [[0,0,0],[1,1,0],[1,1,0]]
**输出：** 4

示例 3：

**输入：** grid = [[1,0,0],[1,1,0],[1,1,0]]
**输出：** -1

提示：

  • n == grid.length
  • n == grid[i].length
  • 1 <= n <= 100
  • grid[i][j] 为 0 或 1

方法一：广度优先搜索

把单元格当成图的节点，如果两个相邻单元格的值都是 0，那么这两个相邻单元格代表的节点之间存在边，且边长为 1。因此问题可以转化为给定一个无权图，求两个节点的最短路径。求无权图的最短路径问题的解法是广度优先搜索 。

首先如果 grid}[0][0] = 1，那么显然不存在最短路径，因此返回 -1。使用 dist}[x][y] 保存左上角单元格 (0, 0) 到某一单元格 (x, y) 的最短路径，初始时 dist}[0][0] = 1。首先，我们将单元格 (0, 0) 放入队列中，然后不断执行以下操作：

  1. 如果队列为空，那么返回 -1。

  2. 从队列中取出单元格 (x, y)，如果该单元格等于右下角单元格，那么返回 dist}[x][y]。

  3. 遍历该单元格的所有相邻单元格，如果相邻单元格 (x_1, y_1) 的值为 0 且未被访问，那么令 dist}[x_1][y_1] = \textit{dist}[x][y] + 1，并且将相邻单元格 (x_1, y_1) 放入队列中。

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    int shortestPathBinaryMatrix(vector<vector<int>>& grid) {
        if (grid[0][0] == 1) {
            return -1;
        }
        int n = grid.size();
        vector<vector<int>> dist(n, vector<int>(n, INT_MAX));
        queue<pair<int, int>> q;
        q.push({0, 0});
        dist[0][0] = 1;
        while (!q.empty()) {
            auto [x, y] = q.front();
            q.pop();
            if (x == n - 1 && y == n - 1) {
                return dist[x][y];
            }
            for (int dx = -1; dx <= 1; dx++) {
                for (int dy = -1; dy <= 1; dy++) {
                    if (x + dx < 0 || x + dx >= n || y + dy < 0 || y + dy >= n) { // 越界
                        continue;
                    }
                    if (grid[x + dx][y + dy] == 1 || dist[x + dx][y + dy] <= dist[x][y] + 1) { // 单元格值不为 0 或已被访问
                        continue;
                    }
                    dist[x + dx][y + dy] = dist[x][y] + 1;
                    q.push({x + dx, y + dy});
                }
            }
        }
        return -1;
    }
};
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
    public int shortestPathBinaryMatrix(int[][] grid) {
        if (grid[0][0] == 1) {
            return -1;
        }
        int n = grid.length;
        int[][] dist = new int[n][n];
        for (int i = 0; i < n; i++) {
            Arrays.fill(dist[i], Integer.MAX_VALUE);
        }
        Queue<int[]> queue = new ArrayDeque<int[]>();
        queue.offer(new int[]{0, 0});
        dist[0][0] = 1;
        while (!queue.isEmpty()) {
            int[] arr = queue.poll();
            int x = arr[0], y = arr[1];
            if (x == n - 1 && y == n - 1) {
                return dist[x][y];
            }
            for (int dx = -1; dx <= 1; dx++) {
                for (int dy = -1; dy <= 1; dy++) {
                    if (x + dx < 0 || x + dx >= n || y + dy < 0 || y + dy >= n) { // 越界
                        continue;
                    }
                    if (grid[x + dx][y + dy] == 1 || dist[x + dx][y + dy] <= dist[x][y] + 1) { // 单元格值不为 0 或已被访问
                        continue;
                    }
                    dist[x + dx][y + dy] = dist[x][y] + 1;
                    queue.offer(new int[]{x + dx, y + dy});
                }
            }
        }
        return -1;
    }
}
[sol1-C#]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public class Solution {
    public int ShortestPathBinaryMatrix(int[][] grid) {
        if (grid[0][0] == 1) {
            return -1;
        }
        int n = grid.Length;
        int[][] dist = new int[n][];
        for (int i = 0; i < n; i++) {
            dist[i] = new int[n];
            Array.Fill(dist[i], int.MaxValue);
        }
        Queue<Tuple<int, int>> queue = new Queue<Tuple<int, int>>();
        queue.Enqueue(new Tuple<int, int>(0, 0));
        dist[0][0] = 1;
        while (queue.Count > 0) {
            Tuple<int, int> tuple = queue.Dequeue();
            int x = tuple.Item1, y = tuple.Item2;
            if (x == n - 1 && y == n - 1) {
                return dist[x][y];
            }
            for (int dx = -1; dx <= 1; dx++) {
                for (int dy = -1; dy <= 1; dy++) {
                    if (x + dx < 0 || x + dx >= n || y + dy < 0 || y + dy >= n) { // 越界
                        continue;
                    }
                    if (grid[x + dx][y + dy] == 1 || dist[x + dx][y + dy] <= dist[x][y] + 1) { // 单元格值不为 0 或已被访问
                        continue;
                    }
                    dist[x + dx][y + dy] = dist[x][y] + 1;
                    queue.Enqueue(new Tuple<int, int>(x + dx, y + dy));
                }
            }
        }
        return -1;
    }
}
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution:
    def shortestPathBinaryMatrix(self, grid: List[List[int]]) -> int:
        if grid[0][0] == 1:
            return -1
        n = len(grid)
        dist = [[inf] * n for _ in range(n)]
        dist[0][0] = 1
        queue = deque([(0, 0)])
        while queue:
            x, y = queue.popleft()
            if x == y == n - 1:
                return dist[x][y]
            for dx in range(-1, 2):
                for dy in range(-1, 2):
                    if x + dx < 0 or x + dx >= n or y + dy < 0 or y + dy >= n: # 越界
                        continue
                    if (grid[x + dx][y + dy] == 1 or dist[x + dx][y + dy] <= dist[x][y] + 1): # 单元格值不为 0 或已被访问
                        continue
                    dist[x + dx][y + dy] = dist[x][y] + 1
                    queue.append((x + dx, y + dy))
        return -1

[sol1-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
var shortestPathBinaryMatrix = function(grid) {
    if (grid[0][0] === 1) {
        return -1;
    }
    const n = grid.length;
    const dist = new Array(n).fill(undefined).map(() => new Array(n).fill(Infinity));
    dist[0][0] = 1;
    const queue = [[0, 0]];
    while (queue.length > 0) {
        const [x, y] = queue.shift();
        for (let dx = -1; dx <= 1; dx++) {
            for (let dy = -1; dy <= 1; dy++) {
                if (x == n - 1 && y == n - 1) {
                    return dist[x][y];
                }
                if (x + dx < 0 || x + dx >= n || y + dy < 0 || y + dy >= n) { // 越界
                    continue;
                }
                if (grid[x + dx][y + dy] > 0 || dist[x + dx][y + dy] <= dist[x][y] + 1) { // 单元格值不为 0 或已被访问
                    continue;
                }
                dist[x + dx][y + dy] = dist[x][y] + 1;
                queue.push([x + dx, y + dy]);
            }
        }
    }
    return -1;
}
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
func shortestPathBinaryMatrix(grid [][]int) int {
    if grid[0][0] == 1 {
        return -1
    }
    n := len(grid)
    dist := make([][]int, n)
    for i := 0; i < n; i++ {
        dist[i] = make([]int, n)
        for j := 0; j < n; j++ {
            dist[i][j] = 0x3f3f3f3f
        }
    }
    q := [][2]int{ {0, 0} }
    dist[0][0] = 1
    for len(q) > 0 {
        x, y := q[0][0], q[0][1]
        q = q[1:]
        if x == n - 1 && y == n - 1 {
            return dist[x][y]
        }
        for dx := -1; dx <= 1; dx++ {
            for dy := -1; dy <= 1; dy++ {
                if x + dx < 0 || x + dx >= n || y + dy < 0 || y + dy >= n { // 越界
                    continue
                }
                if grid[x + dx][y + dy] == 1 || dist[x][y] + 1 >= dist[x + dx][y + dy] { // 单元格值不为 0 或已被访问
                    continue
                }
                dist[x + dx][y + dy] = dist[x][y] + 1
                q = append(q, [2]int{x + dx, y + dy})
            }
        }
    }
    return -1
}
[sol1-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
const int INF = 0x3f3f3f3f;

typedef struct Pair {
    int first;
    int second;
} Pair;

int shortestPathBinaryMatrix(int** grid, int gridSize, int* gridColSize) {
    if (grid[0][0] == 1) {
        return -1;
    }

    int n = gridSize;
    int dist[n][n];
    Pair queue[n * n];
    int head = 0, tail = 0;

    memset(dist, 0x3f, sizeof(dist));
    queue[tail].first = 0;
    queue[tail].second = 0;
    tail++;
    dist[0][0] = 1;
    while (head != tail) {
        int x = queue[head].first;
        int y = queue[head].second;
        head++;
        if (x == n - 1 && y == n - 1) {
            return dist[x][y];
        }
        for (int dx = -1; dx <= 1; dx++) {
            for (int dy = -1; dy <= 1; dy++) {
                if (x + dx < 0 || x + dx >= n || y + dy < 0 || y + dy >= n) { // 越界
                    continue;
                }
                if (grid[x + dx][y + dy] == 1 || dist[x + dx][y + dy] <= dist[x][y] + 1) { // 单元格值不为 0 或已被访问
                    continue;
                }
                dist[x + dx][y + dy] = dist[x][y] + 1;
                queue[tail].first = x + dx;
                queue[tail].second = y + dy;
                tail++;
            }
        }
    }
    return -1;
}

复杂度分析

  • 时间复杂度：O(n^2)，其中 n 是数组的行数或列数。广度优先搜索最多访问 n^2 个单元格。

  • 空间复杂度：O(n^2)。队列 q 不超过 n^2 个元素，保存 dist 需要 O(n^2) 的空间，保存队列 q 需要 O(n^2) 的空间。

 Comments
On this page
1091-二进制矩阵中的最短路径