(这是一个 **交互式问题 **)
给你一个 山脉数组 mountainArr,请你返回能够使得 mountainArr.get(index) 等于
target 最小 的下标 index 值。
如果不存在这样的下标 index,就请返回 -1。
何为山脉数组?如果数组 A 是一个山脉数组的话,那它满足如下条件:
首先 ,A.length >= 3
其次 ,在 0 < i < A.length - 1 条件下,存在 i 使得:
A[0] < A[1] < ... A[i-1] < A[i]A[i] > A[i+1] > ... > A[A.length - 1]
你将 不能直接访问该山脉数组 ,必须通过 MountainArray 接口来获取数据:
MountainArray.get(k) - 会返回数组中索引为k 的元素(下标从 0 开始)MountainArray.length() - 会返回该数组的长度
注意:
对 MountainArray.get 发起超过 100
次调用的提交将被视为错误答案。此外,任何试图规避判题系统的解决方案都将会导致比赛资格被取消。
为了帮助大家更好地理解交互式问题,我们准备了一个样例 “ 答案 “:<https://leetcode-
cn.com/playground/RKhe3ave>,请注意这 不是一个正确答案 。
示例 1:
**输入:** array = [1,2,3,4,5,3,1], target = 3
**输出:** 2
**解释:** 3 在数组中出现了两次,下标分别为 2 和 5,我们返回最小的下标 2。
示例 2:
**输入:** array = [0,1,2,4,2,1], target = 3
**输出:** -1
**解释:** 3 在数组中没有出现,返回 -1。
提示:
3 <= mountain_arr.length() <= 100000 <= target <= 10^90 <= mountain_arr.get(index) <= 10^9
📺 视频题解

📖 文字题解
方法一:二分查找
思路
显然,如果山脉数组是一个单调递增或者单调递减的序列,那么我们可以通过二分法迅速找到目标值。
而现在题目中有一个单调递增序列(峰值左边)和一个单调递减序列(峰值右边),我们只是不知道两个序列的分割点,即峰值在哪里。所以我们第一步应该首先找到峰值。
而峰值也可以使用二分法寻找:
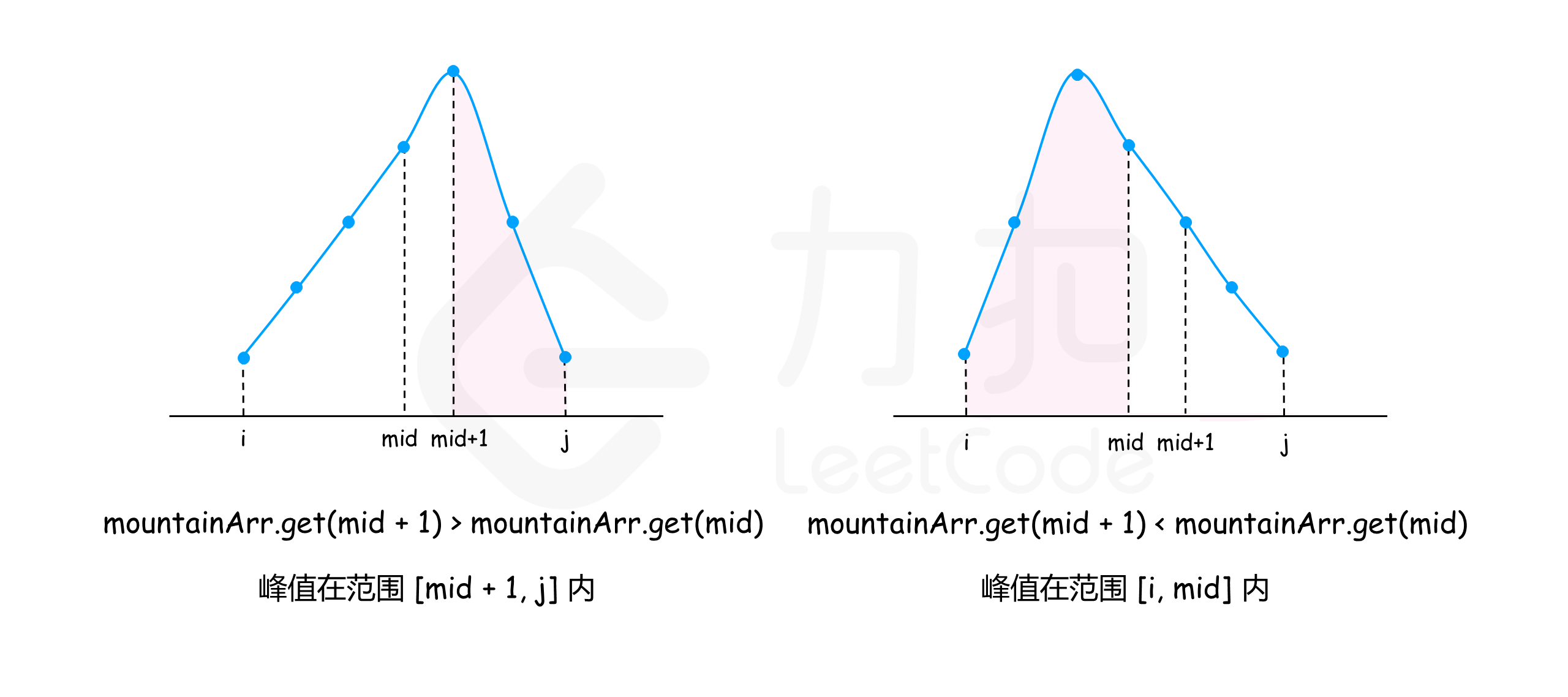
对于一个范围 [i, j],我们可以先找到范围 [i, j] 中间连续的两个点 mid 与 mid + 1。如果 mountainArr.get(mid + 1) > mountainArr.get(mid),那么可以知道峰值在范围 [mid + 1, j] 内;如果 mountainArr.get(mid + 1) < mountainArr.get(mid),那么可以知道峰值在范围 [i, mid] 内。通过这样的方法,我们可以在 O(\log n) 的时间内找到峰值所处的下标。

这个方法的正确性在于我们二分的目标是相邻位置数的差值,我们每次判断的是 mountainArr.get(mid + 1) - mountainArr.get(mid) 与 0 的大小关系。这个差值组成的数组保证了单调递增的部分差值均为正数,单调递减的部分差值均为负数,整个数组呈现 [正数,正数,正数,...,负数,负数] 这样前半部分均为正数,后半部分均为负数的性质,满足单调性,因此我们可以使用二分查找。
以示例 1 为例,我们对整个数组进行差分,即除了第一个数每个数都减去前一个数得到新的数组,最终我们得到 [1, 1, 1, 1, -2, -2],整个差分数组满足单调性,可以应用二分法。
接下来我们只需要使用二分法在单调序列中找到目标值即可,注意二分法要使用两次,为了编码简洁可以将二分法封装成函数。
算法
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| class Solution {
int binary_search(MountainArray &mountain, int target, int l, int r, int key(int)) {
target = key(target);
while (l <= r) {
int mid = (l + r) / 2;
int cur = key(mountain.get(mid));
if (cur == target) {
return mid;
} else if (cur < target) {
l = mid + 1;
} else {
r = mid - 1;
}
}
return -1;
}
public:
int findInMountainArray(int target, MountainArray &mountainArr) {
int l = 0, r = mountainArr.length() - 1;
while (l < r) {
int mid = (l + r) / 2;
if (mountainArr.get(mid) < mountainArr.get(mid + 1)) {
l = mid + 1;
} else {
r = mid;
}
}
int peak = l;
int index = binary_search(mountainArr, target, 0, peak, [](int x) -> int{return x;});
if (index != -1) {
return index;
}
return binary_search(mountainArr, target, peak + 1, mountainArr.length() - 1, [](int x) -> int{return -x;});
}
};
|
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| class Solution {
public int findInMountainArray(int target, MountainArray mountainArr) {
int l = 0, r = mountainArr.length() - 1;
while (l < r) {
int mid = (l + r) / 2;
if (mountainArr.get(mid) < mountainArr.get(mid + 1)) {
l = mid + 1;
} else {
r = mid;
}
}
int peak = l;
int index = binarySearch(mountainArr, target, 0, peak, true);
if (index != -1) {
return index;
}
return binarySearch(mountainArr, target, peak + 1, mountainArr.length() - 1, false);
}
public int binarySearch(MountainArray mountainArr, int target, int l, int r, boolean flag) {
if (!flag) {
target *= -1;
}
while (l <= r) {
int mid = (l + r) / 2;
int cur = mountainArr.get(mid) * (flag ? 1 : -1);
if (cur == target) {
return mid;
} else if (cur < target) {
l = mid + 1;
} else {
r = mid - 1;
}
}
return -1;
}
}
|
[sol1-Python3]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| def binary_search(mountain, target, l, r, key=lambda x: x):
target = key(target)
while l <= r:
mid = (l + r) // 2
cur = key(mountain.get(mid))
if cur == target:
return mid
elif cur < target:
l = mid + 1
else:
r = mid - 1
return -1
class Solution:
def findInMountainArray(self, target: int, mountain_arr: 'MountainArray') -> int:
l, r = 0, mountain_arr.length() - 1
while l < r:
mid = (l + r) // 2
if mountain_arr.get(mid) < mountain_arr.get(mid + 1):
l = mid + 1
else:
r = mid
peak = l
index = binary_search(mountain_arr, target, 0, peak)
if index != -1:
return index
index = binary_search(mountain_arr, target, peak + 1, mountain_arr.length() - 1, lambda x: -x)
return index
|
复杂度分析