如果你熟悉 Shell 编程,那么一定了解过花括号展开,它可以用来生成任意字符串。
花括号展开的表达式可以看作一个由 花括号 、 逗号 和 小写英文字母 组成的字符串,定义下面几条语法规则:
- 如果只给出单一的元素
x,那么表达式表示的字符串就只有 "x"。R(x) = {x}
- 例如,表达式
"a" 表示字符串 "a"。
- 而表达式
"w" 就表示字符串 "w"。
- 当两个或多个表达式并列,以逗号分隔,我们取这些表达式中元素的并集。
R({e_1,e_2,...}) = R(e_1) ∪ R(e_2) ∪ ...
- 例如,表达式
"{a,b,c}" 表示字符串 "a","b","c"。
- 而表达式
"{ {a,b},{b,c} }" 也可以表示字符串 "a","b","c"。
- 要是两个或多个表达式相接,中间没有隔开时,我们从这些表达式中各取一个元素依次连接形成字符串。
R(e_1 + e_2) = {a + b for (a, b) in R(e_1) × R(e_2)}
- 例如,表达式
"{a,b}{c,d}" 表示字符串 "ac","ad","bc","bd"。
- 表达式之间允许嵌套,单一元素与表达式的连接也是允许的。
- 例如,表达式
"a{b,c,d}" 表示字符串 "ab","ac","ad"。
- 例如,表达式
"a{b,c}{d,e}f{g,h}" 可以表示字符串 "abdfg", "abdfh", "abefg", "abefh", "acdfg", "acdfh", "acefg", "acefh"。
给出表示基于给定语法规则的表达式 expression,返回它所表示的所有字符串组成的有序列表。
假如你希望以「集合」的概念了解此题,也可以通过点击 “ 显示英文描述 ” 获取详情。
示例 1:
**输入:** expression = "{a,b}{c,{d,e} }"
**输出:** ["ac","ad","ae","bc","bd","be"]
示例 2:
**输入:** expression = "{ {a,z},a{b,c},{ab,z} }"
**输出:** ["a","ab","ac","z"]
**解释:** 输出中 **不应** 出现重复的组合结果。
提示:
1 <= expression.length <= 60expression[i] 由 '{','}',',' 或小写英文字母组成- 给出的表达式
expression 用以表示一组基于题目描述中语法构造的字符串
方法一:递归解析
思路与算法
表达式可以拆分为多个子表达式,以逗号分隔或者直接相接。我们应当先按照逗号分割成多个子表达式进行求解,然后再对所有结果求并集。这样做的原因是求积的优先级高于求并集的优先级。
我们用 expr 表示一个任意一种表达式,用 term 表示一个最外层没有逗号分割的表达式,那么 expr 可以按照如下规则分解:
expr} \rightarrow \textit{term}|\textit{term}, \textit{expr
其中的 | 表示或者,即 expr 可以分解为前者,也可以分解为后者。
再来看 term, term 可以由小写英文字母或者花括号包括的表达式直接相接组成,我们用 item 来表示每一个相接单元,那么 term 可以按照如下规则分解:
term} \rightarrow \textit{item}|\textit{item}~\textit{term
item 可以进一步分解为小写英文字母 letter 或者花括号包括的表达式,它的分解如下:
item} \rightarrow \textit{letter}|{expr\
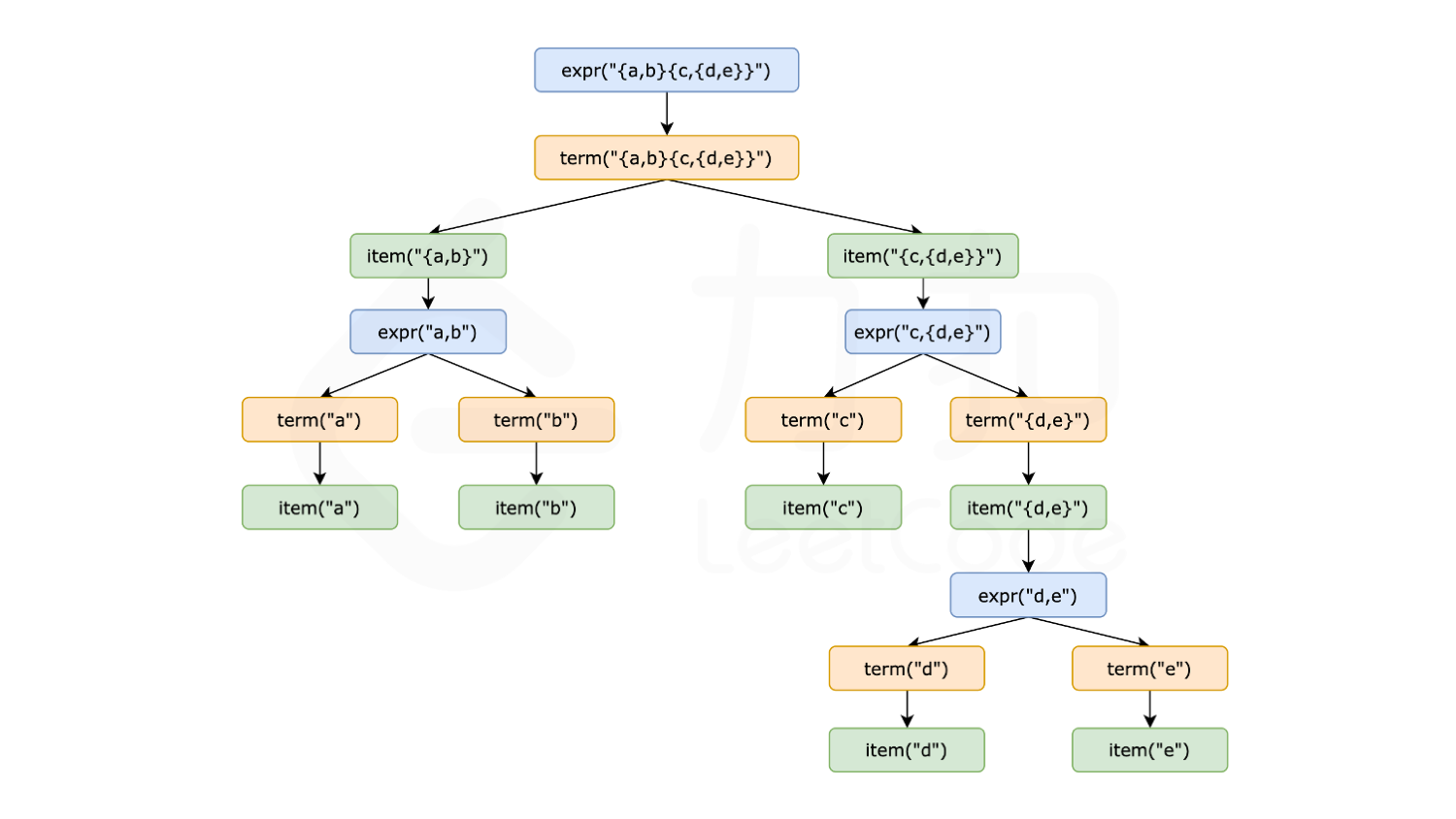
在代码中,我们编写三个函数,分别负责以上三种规则的分解:
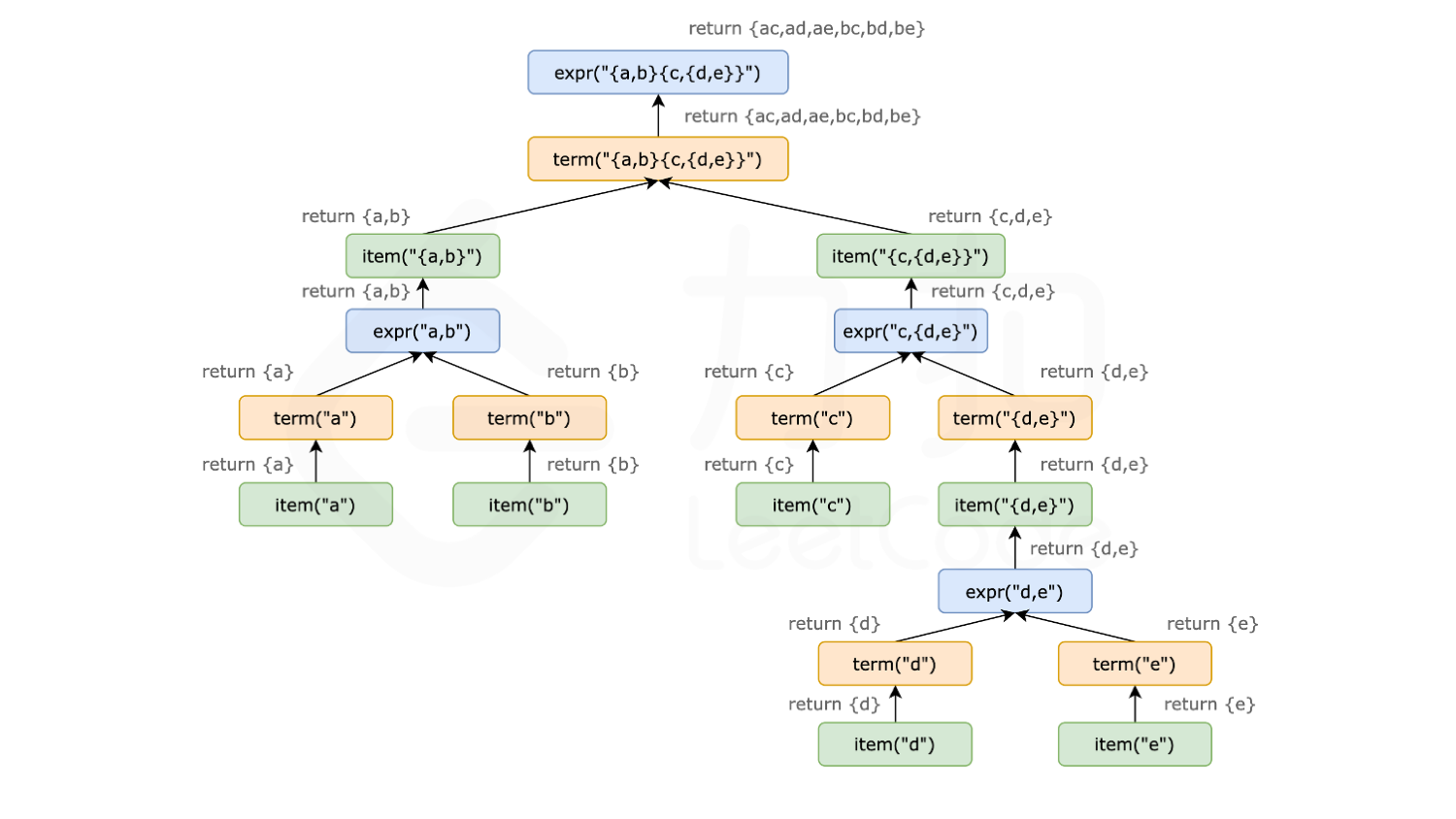
- expr 函数,不断的调用 term,并与其结果进行合并。如果匹配到表达式末尾或者当前字符不是逗号时,则返回。
- term 函数,不断的调用 item,并与其结果求积。如果匹配到表达式末尾或者当前字符不是小写字母,并且也不是左括号时,则返回。
- item 函数,根据当前字符是不是左括号来求解。如果是左括号,则调用 expr,返回结果;否则构造一个只包含当前字符的字符串集合,返回结果。
以下示意图以 {a,b}{c,{d,e}\ 为例,展示了表达式递归拆解以及回溯的全过程。
< ,
, >
>
在代码实现过程中有以下细节:
- 维护一个外部指针来遍历整个表达式,或者将表达式和当前遍历下标以引用的方式传递给被调函数。
- 因为最终答案需要去重,所以可以先用集合来求解中间结果,最后再转换成已排序的列表作为最终答案。
代码
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
| class Solution {
string expression;
int idx;
set<string> item() {
set<string> ret;
if (expression[idx] == '{') {
idx++;
ret = expr();
} else {
ret = {string(1, expression[idx])};
}
idx++;
return move(ret);
}
set<string> term() {
set<string> ret = {""};
while (idx < expression.size() && (expression[idx] == '{' || isalpha(expression[idx]))) {
auto sub = item();
set<string> tmp;
for (auto &left : ret) {
for (auto &right : sub) {
tmp.insert(left + right);
}
}
ret = move(tmp);
}
return move(ret);
}
set<string> expr() {
set<string> ret;
while (true) {
ret.merge(term());
if (idx < expression.size() && expression[idx] == ',') {
idx++;
continue;
} else {
break;
}
}
return move(ret);
}
public:
vector<string> braceExpansionII(string expression) {
this->expression = expression;
this->idx = 0;
auto ret = expr();
return {ret.begin(), ret.end()};
}
};
|
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| class Solution {
String expression;
int idx;
public List<String> braceExpansionII(String expression) {
this.expression = expression;
this.idx = 0;
Set<String> ret = expr();
return new ArrayList<String>(ret);
}
private Set<String> item() {
Set<String> ret = new TreeSet<String>();
if (expression.charAt(idx) == '{') {
idx++;
ret = expr();
} else {
StringBuilder sb = new StringBuilder();
sb.append(expression.charAt(idx));
ret.add(sb.toString());
}
idx++;
return ret;
}
private Set<String> term() {
Set<String> ret = new TreeSet<String>() { {
add("");
} };
while (idx < expression.length() && (expression.charAt(idx) == '{' || Character.isLetter(expression.charAt(idx)))) {
Set<String> sub = item();
Set<String> tmp = new TreeSet<String>();
for (String left : ret) {
for (String right : sub) {
tmp.add(left + right);
}
}
ret = tmp;
}
return ret;
}
private Set<String> expr() {
Set<String> ret = new TreeSet<String>();
while (true) {
ret.addAll(term());
if (idx < expression.length() && expression.charAt(idx) == ',') {
idx++;
continue;
} else {
break;
}
}
return ret;
}
}
|
复杂度分析
方法二:栈
思路与算法
如果把题目中的表达式并列关系看做是求和,把相接看做是求积,那么求解整个表达式的过程可以类比于求解中缀表达式的过程,例如:{a,b}{c,{d,e}\ 可以看做是 {a,b} \times {c + {d + e}\。
与求解中缀表达式一样,在遍历表达式的过程中我们需要用到两个栈,一个用来存放运算符(即加号和乘号,以及左大括号),另一个用来存运算对象(即集合)。
在本题中有一个特殊情况需要处理,就是乘号需要我们自己来添加,我们按照当前字符的种类来判断前面是否需要添加乘号:
- 如果当前字符是
\{",并且前面是 }“ 或者小写英文字母时,需要添加乘号运算。
- 如果当前字符是小写字母,并且前面是 ``}“ 或者是小写英文字母时,需要添加乘号运算。
- 如果当前字符是 ``,” ,则前面一定不需要添加乘号运算。
- 如果当前字符是 ``}“,则前面一定不需要添加乘号运算。
因此,只有当前字符是 ``{“ 或者小写字母时,才需要考虑是否在前面添加乘号。
接下来我们分析运算优先级的问题,在本题中只涉及加法和乘法两种运算。如果一个表达式同时有并列和相接,那我们应该先计算相接的结果,再计算并列的结果。因此,乘法的优先级要大于加法。
至此,我们可以按照如下流程来计算表达式的值:
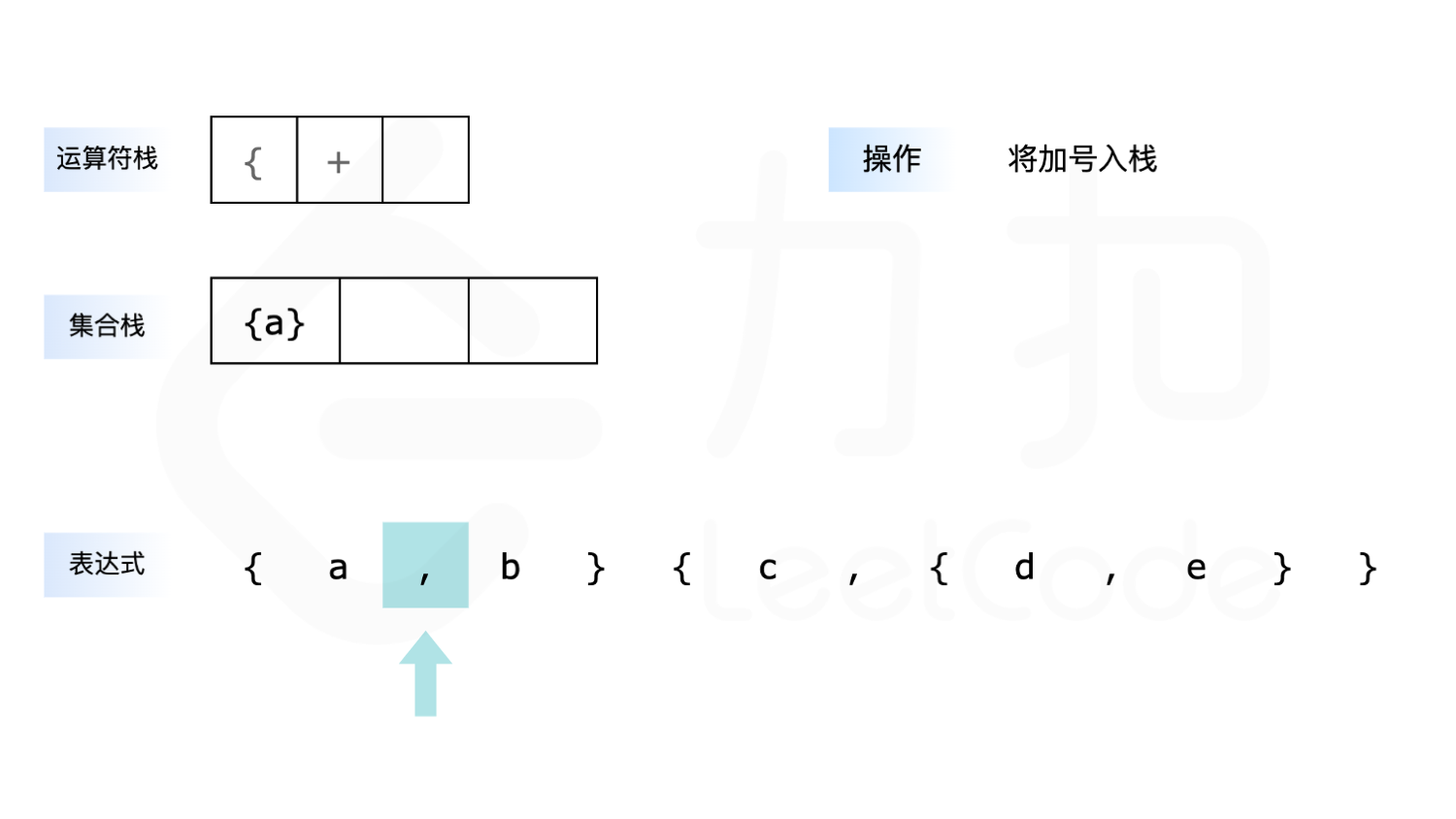
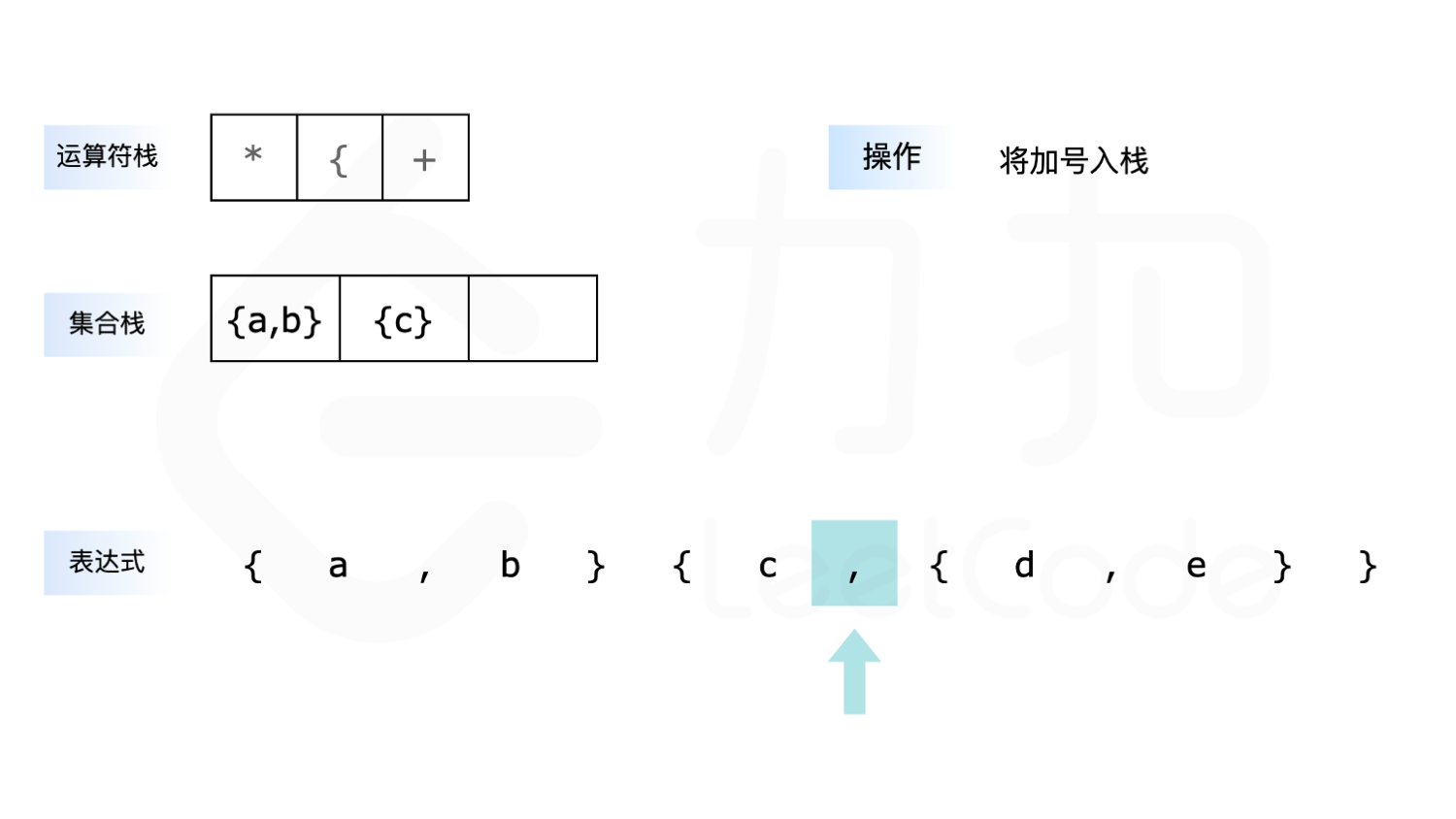
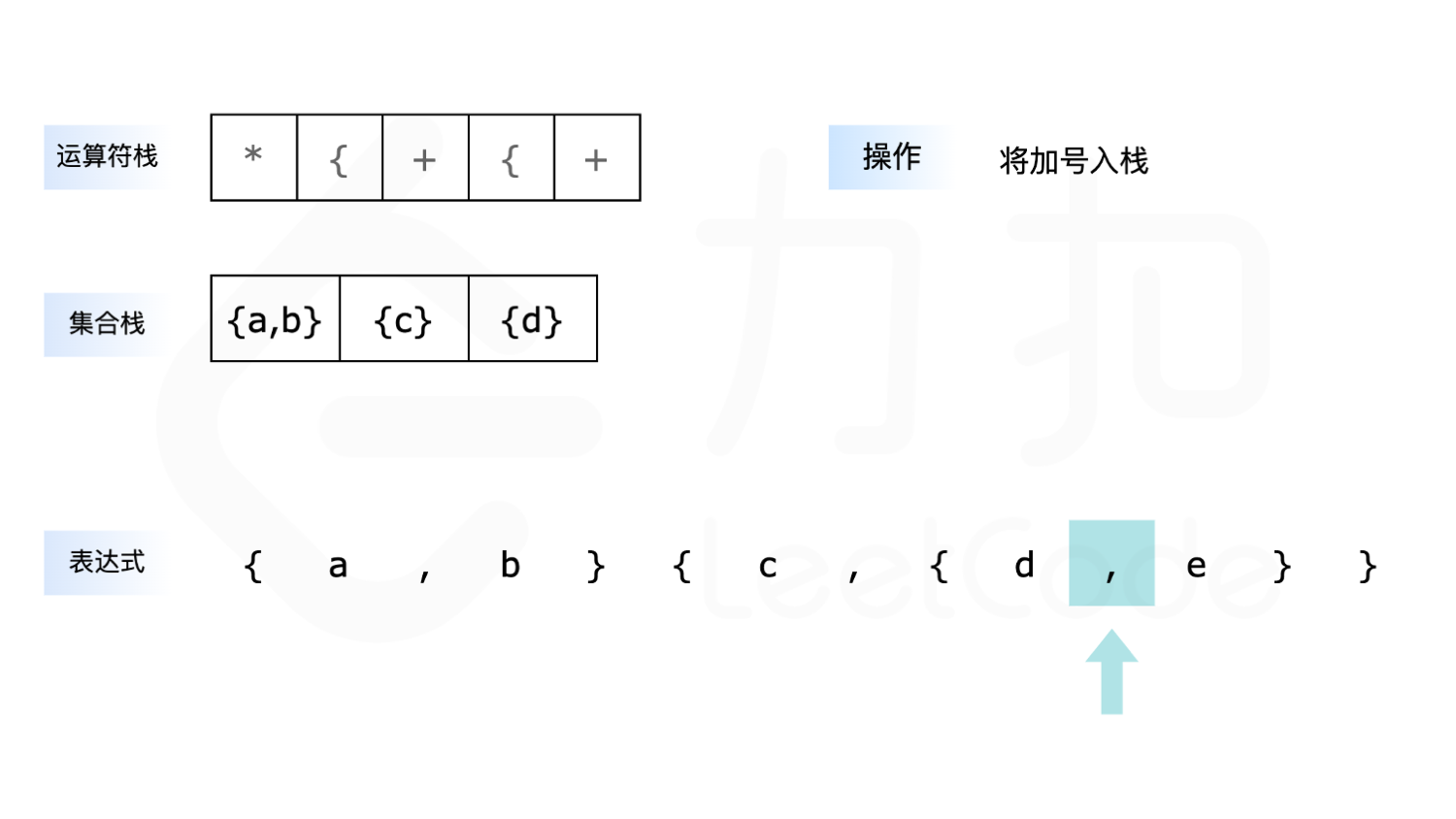
- 如果遇到 ``,”,则先判断运算符栈顶是否是乘号,如果是乘号则需要先计算乘法,直到栈顶不是乘号为止,再将加号放入运算符栈中。
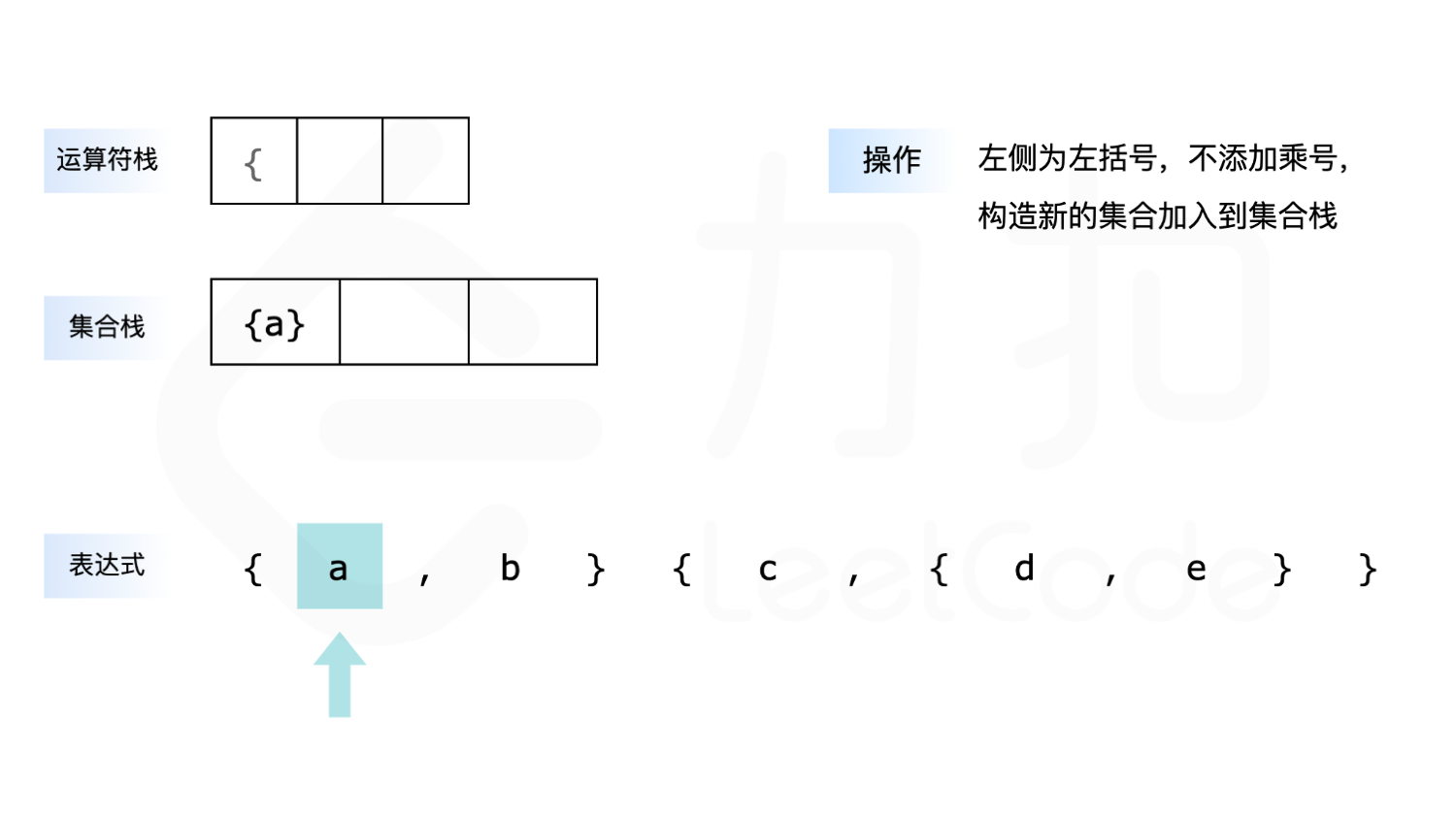
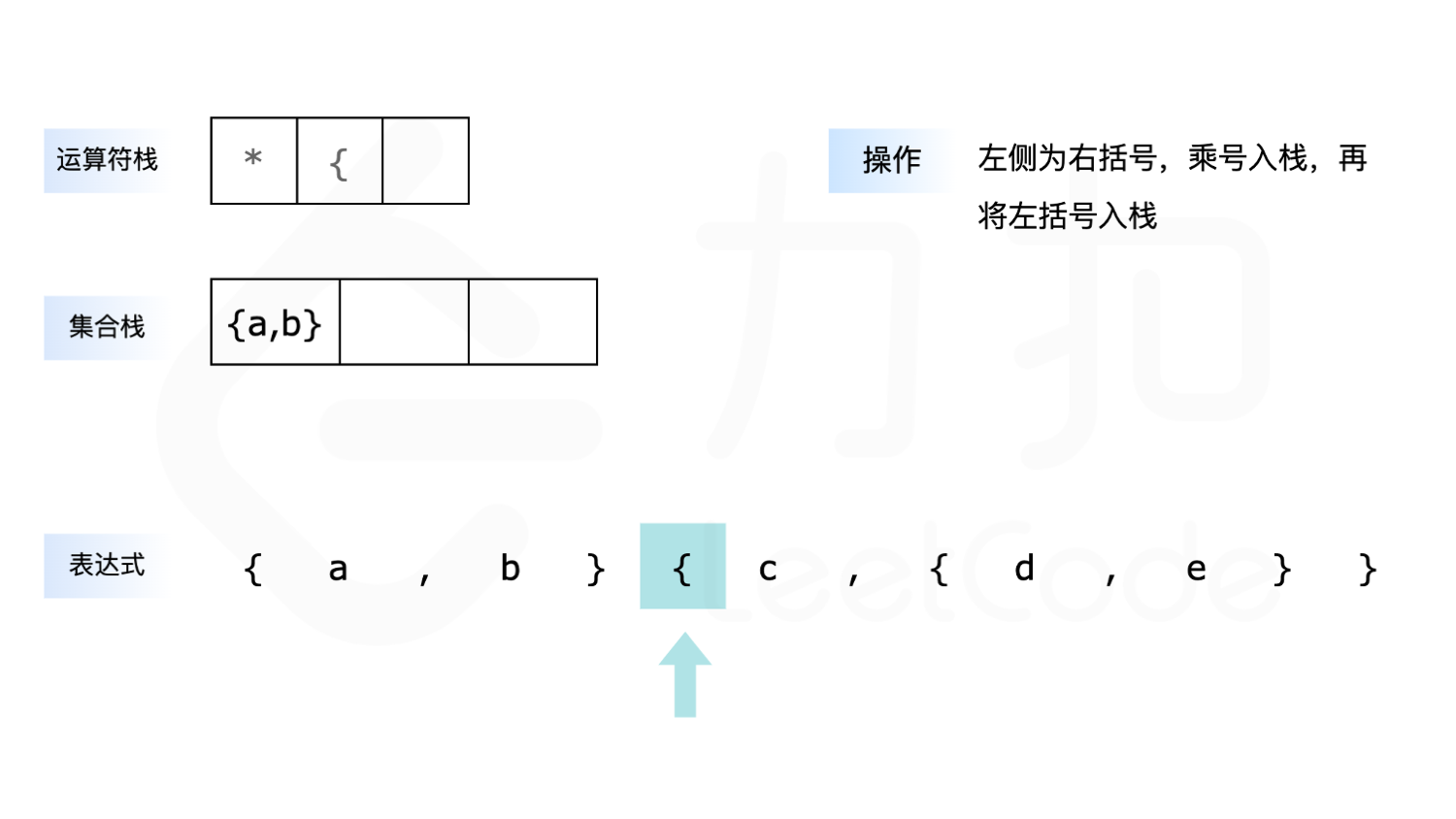
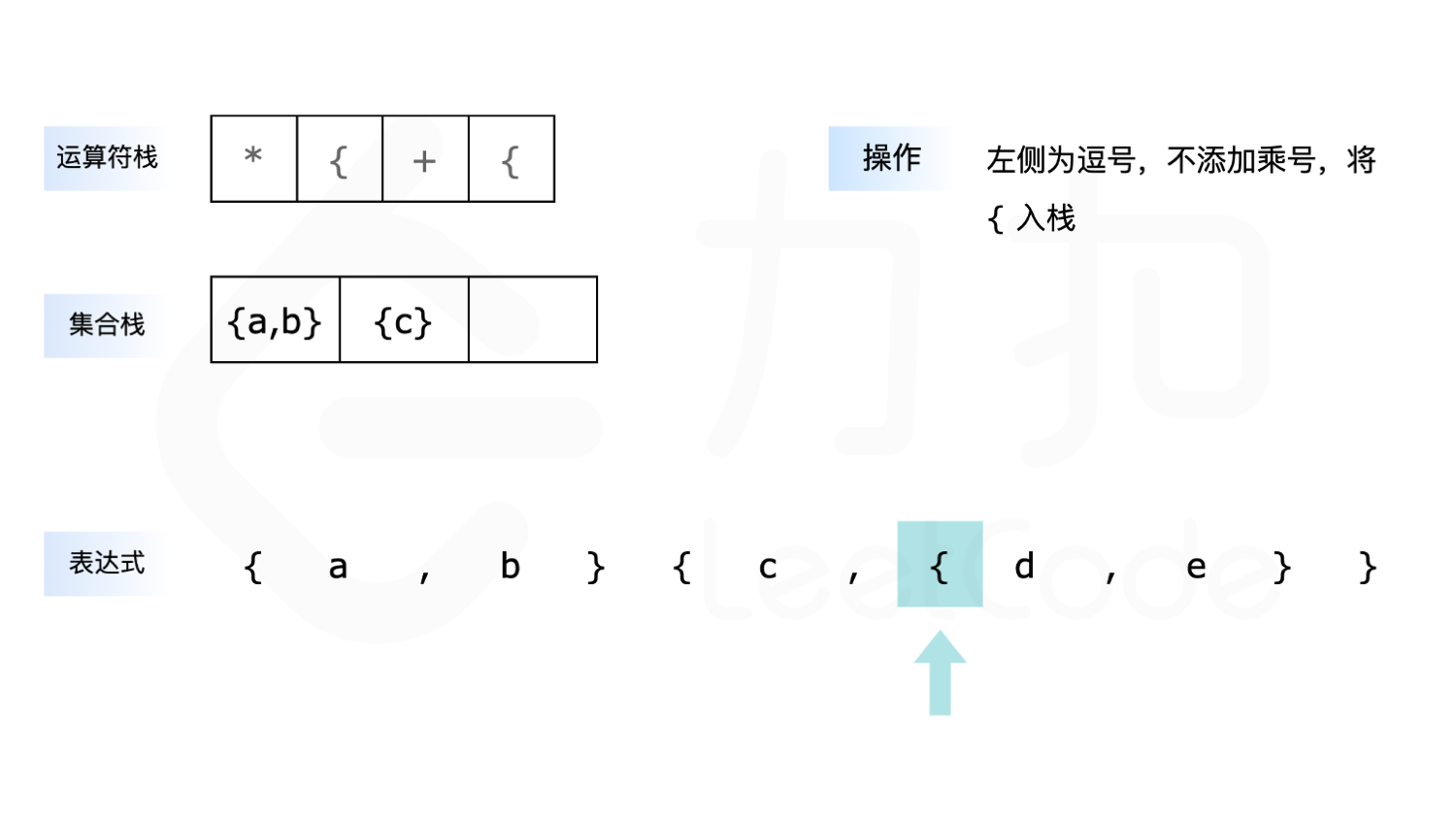
- 如果遇到 ``{“,则先判断是否需要添加乘号,再将 { 放入运算符栈。
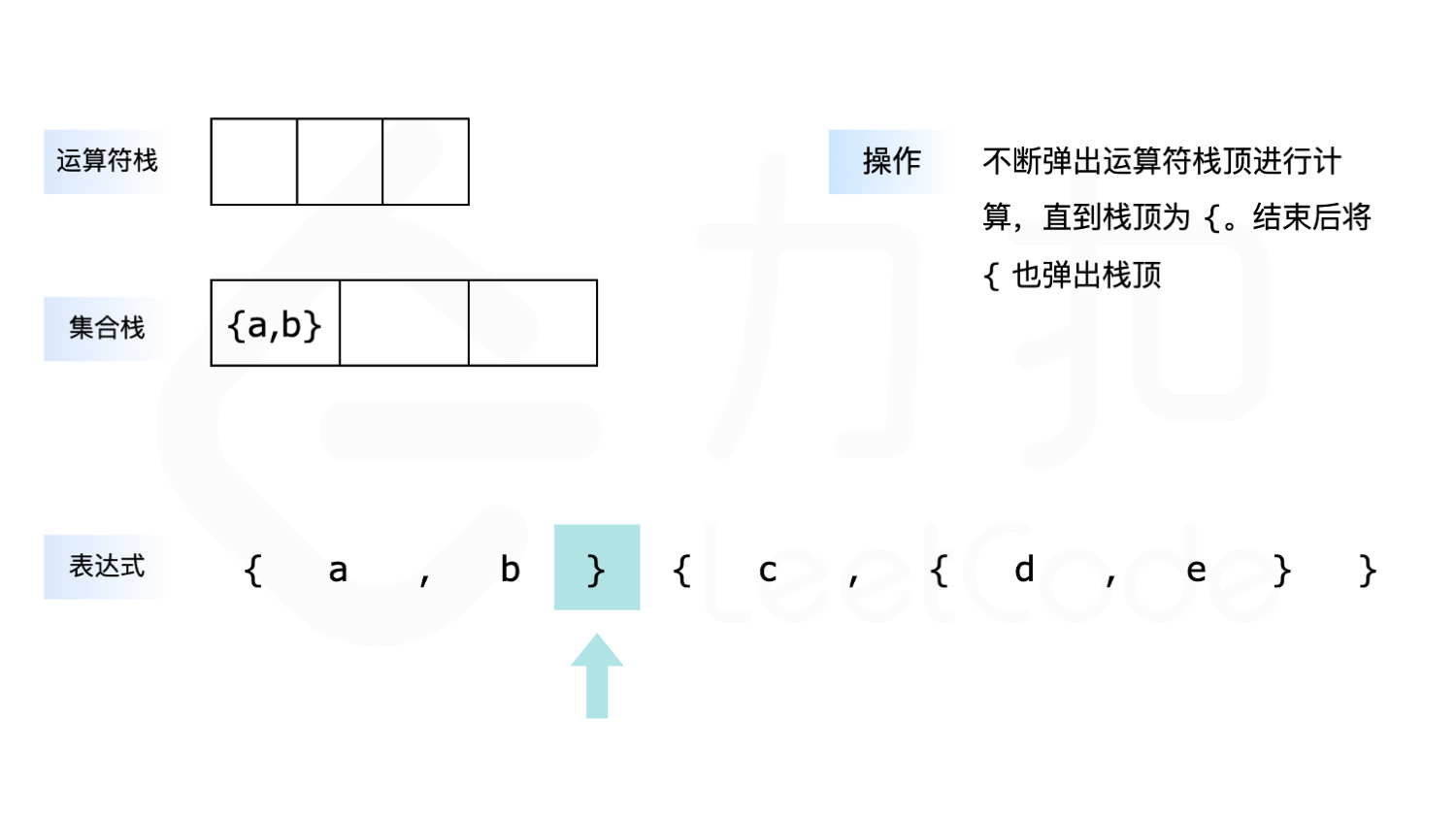
- 如果遇到 ``}“,则不断地弹出运算符栈顶,并进行相应的计算,直到栈顶为左括号为止。
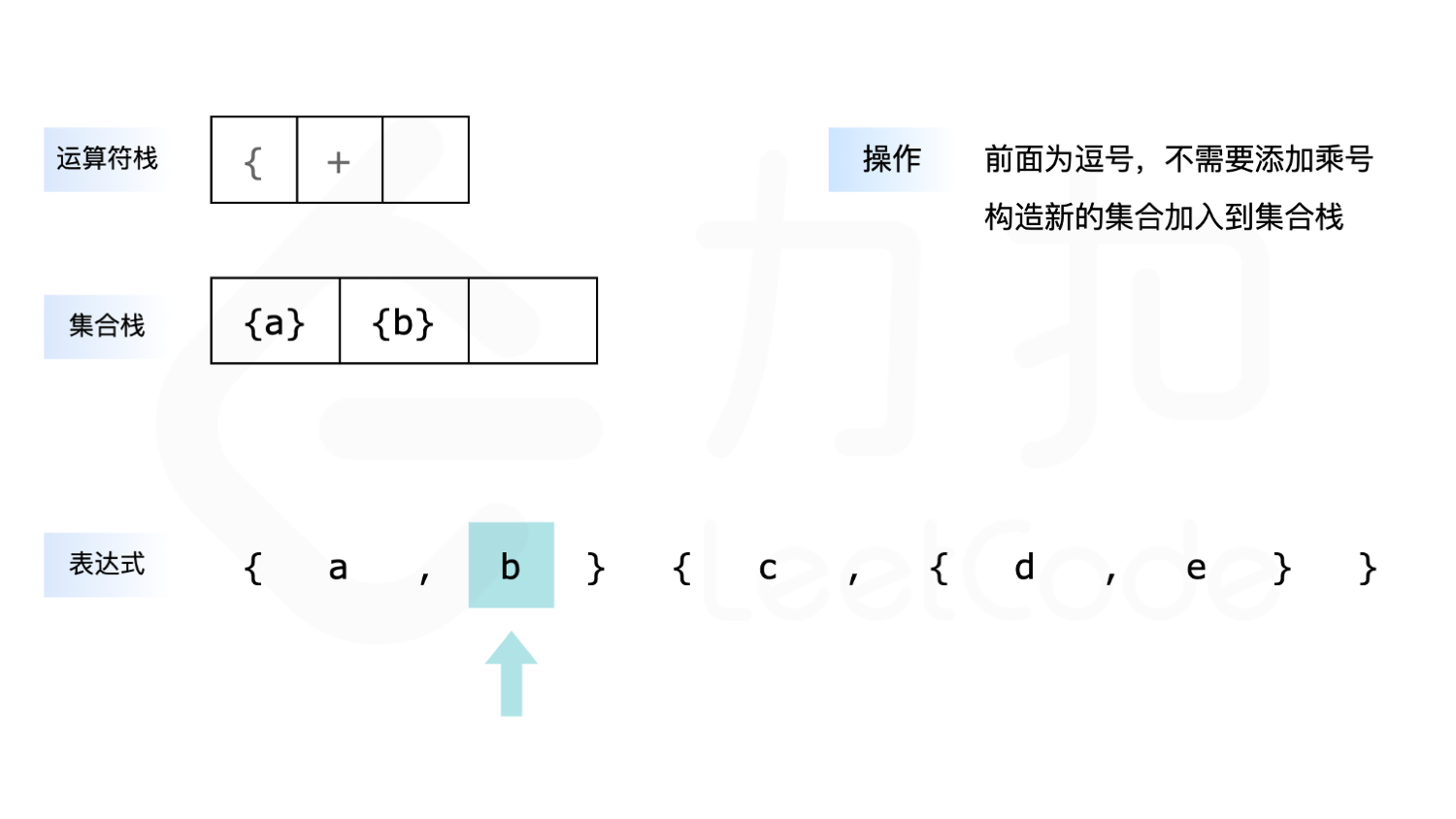
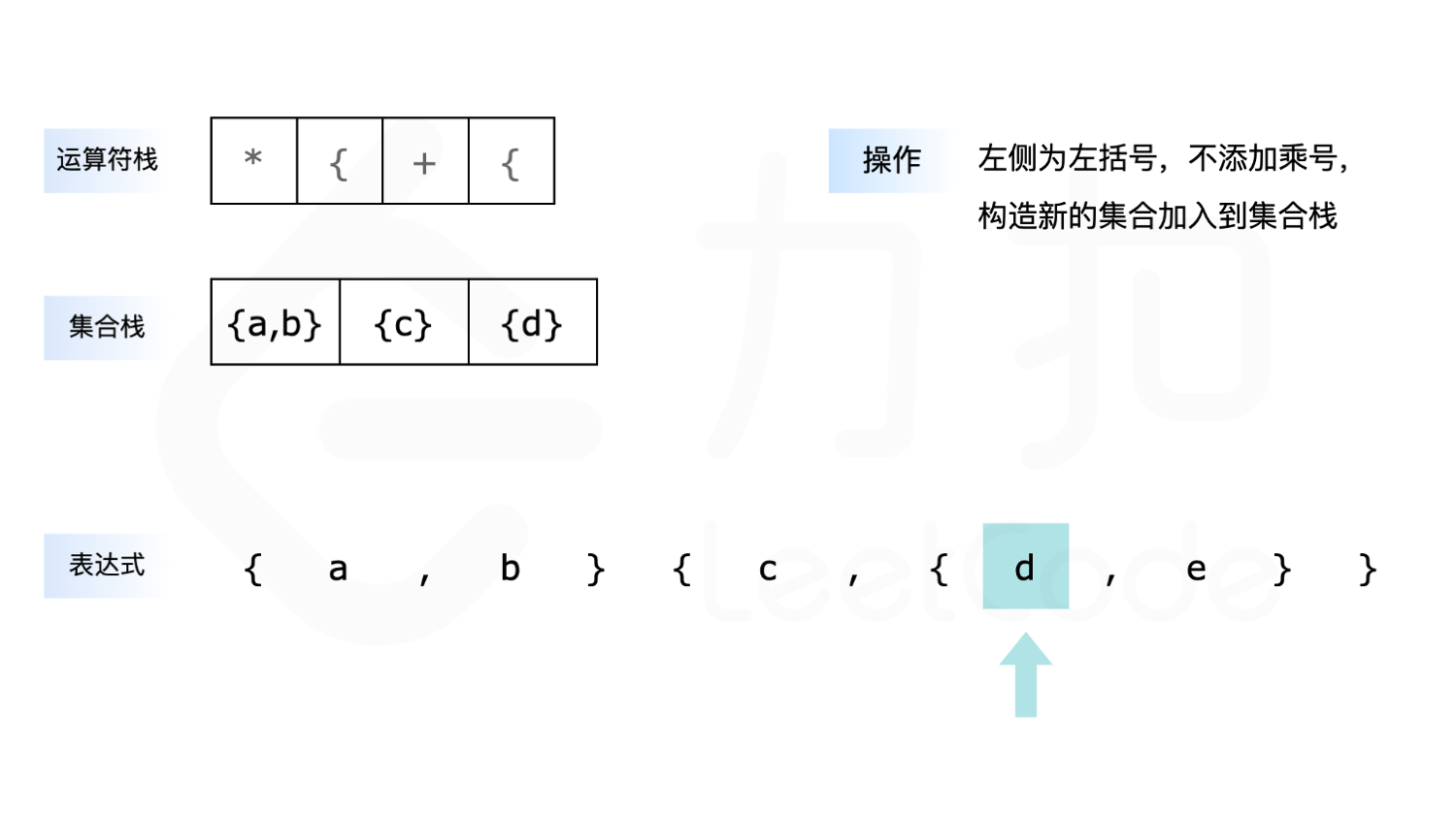
- 如果遇到小写字母,则先判断是否需要添加乘号,再构造一个只包含当前小写字母的字符串集合,放入集合栈中。
按照上述流程遍历完一次之后,由于题目给定的表达式中最外层可能没有大括号,例如 {a,b}{c,{d,e}\,因此运算符栈中可能依然有元素,我们需要依次将他们弹出并进行计算。最终,集合栈栈顶元素即为答案。
下面展示了以 {a,b}{c,{d,e}\ 为例求解的全过程:
< ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>
代码
[sol2-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| class Solution {
public:
vector<string> braceExpansionII(string expression) {
vector<char> op;
vector<set<string>> stk;
auto ope = [&]() {
int l = stk.size() - 2, r = stk.size() - 1;
if (op.back() == '+') {
stk[l].merge(stk[r]);
} else {
set<string> tmp;
for (auto &left : stk[l]) {
for (auto &right : stk[r]) {
tmp.insert(left + right);
}
}
stk[l] = move(tmp);
}
op.pop_back();
stk.pop_back();
};
for (int i = 0; i < expression.size(); i++) {
if (expression[i] == ',') {
while (op.size() && op.back() == '*') {
ope();
}
op.push_back('+');
} else if (expression[i] == '{') {
if (i > 0 && (expression[i - 1] == '}' || isalpha(expression[i - 1]))) {
op.push_back('*');
}
op.push_back('{');
} else if (expression[i] == '}') {
while (op.size() && op.back() != '{') {
ope();
}
op.pop_back();
} else {
if (i > 0 && (expression[i - 1] == '}' || isalpha(expression[i - 1]))) {
op.push_back('*');
}
stk.push_back({string(1, expression[i])});
}
}
while (op.size()) {
ope();
}
return {stk.back().begin(), stk.back().end()};
}
};
|
[sol2-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
| class Solution {
public List<String> braceExpansionII(String expression) {
Deque<Character> op = new ArrayDeque<Character>();
List<Set<String>> stk = new ArrayList<Set<String>>();
for (int i = 0; i < expression.length(); i++) {
if (expression.charAt(i) == ',') {
while (!op.isEmpty() && op.peek() == '*') {
ope(op, stk);
}
op.push('+');
} else if (expression.charAt(i) == '{') {
if (i > 0 && (expression.charAt(i - 1) == '}' || Character.isLetter(expression.charAt(i - 1)))) {
op.push('*');
}
op.push('{');
} else if (expression.charAt(i) == '}') {
while (!op.isEmpty() && op.peek() != '{') {
ope(op, stk);
}
op.pop();
} else {
if (i > 0 && (expression.charAt(i - 1) == '}' || Character.isLetter(expression.charAt(i - 1)))) {
op.push('*');
}
StringBuilder sb = new StringBuilder();
sb.append(expression.charAt(i));
stk.add(new TreeSet<String>() { {
add(sb.toString());
} });
}
}
while (!op.isEmpty()) {
ope(op, stk);
}
return new ArrayList<String>(stk.get(stk.size() - 1));
}
public void ope(Deque<Character> op, List<Set<String>> stk) {
int l = stk.size() - 2, r = stk.size() - 1;
if (op.peek() == '+') {
stk.get(l).addAll(stk.get(r));
} else {
Set<String> tmp = new TreeSet<String>();
for (String left : stk.get(l)) {
for (String right : stk.get(r)) {
tmp.add(left + right);
}
}
stk.set(l, tmp);
}
op.pop();
stk.remove(stk.size() - 1);
}
}
|
复杂度分析
时间复杂度:O(n\log n),其中 n 是 expression 的长度。整个 expression 只会遍历一次,时间复杂度为 O(n),集合合并以及求积运算的时间复杂度为 O(n\log n),因此总的时间复杂度为 O(n \log n)。
空间复杂度:O(n)。过程中用到了两个栈,他们都满足在任意时刻元素个数不超过 O(n),包含 n 个元素的集合的时间复杂度为 O(n),因此总的空间复杂度为 O(n)。
 ,
, >
> ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>