1103-分糖果 II

排排坐，分糖果。

我们买了一些糖果 candies，打算把它们分给排好队的 n = num_people 个小朋友。

给第一个小朋友 1 颗糖果，第二个小朋友 2 颗，依此类推，直到给最后一个小朋友 n 颗糖果。

然后，我们再回到队伍的起点，给第一个小朋友 n + 1 颗糖果，第二个小朋友 n + 2 颗，依此类推，直到给最后一个小朋友 2 * n
颗糖果。

重复上述过程（每次都比上一次多给出一颗糖果，当到达队伍终点后再次从队伍起点开始），直到我们分完所有的糖果。注意，就算我们手中的剩下糖果数不够（不比前一次发出的糖果多），这些糖果也会全部发给当前的小朋友。

返回一个长度为 num_people、元素之和为 candies 的数组，以表示糖果的最终分发情况（即 ans[i] 表示第 i
个小朋友分到的糖果数）。

示例 1：

**输入：** candies = 7, num_people = 4
**输出：** [1,2,3,1]
**解释：**
第一次，ans[0] += 1，数组变为 [1,0,0,0]。
第二次，ans[1] += 2，数组变为 [1,2,0,0]。
第三次，ans[2] += 3，数组变为 [1,2,3,0]。
第四次，ans[3] += 1（因为此时只剩下 1 颗糖果），最终数组变为 [1,2,3,1]。

示例 2：

**输入：** candies = 10, num_people = 3
**输出：** [5,2,3]
**解释：**
第一次，ans[0] += 1，数组变为 [1,0,0]。
第二次，ans[1] += 2，数组变为 [1,2,0]。
第三次，ans[2] += 3，数组变为 [1,2,3]。
第四次，ans[0] += 4，最终数组变为 [5,2,3]。

提示：

• 1 <= candies <= 10^9
• 1 <= num_people <= 1000

方法一：暴力

思路

最直观的方法是不断地遍历数组，如果还有糖就一直分，直到没有糖为止。

[sol1-Python3]

class Solution:
    def distributeCandies(self, candies: int, num_people: int) -> List[int]:
        ans = [0] * num_people
        i = 0
        while candies != 0:
            ans[i % num_people] += min(i + 1, candies)
            candies -= min(i + 1, candies)
            i += 1
        return ans

[sol1-Java]

class Solution {
    public int[] distributeCandies(int candies, int num_people) {
        int[] ans = new int[num_people];
        int i = 0;
        while (candies != 0) {
            ans[i % num_people] += Math.min(candies, i + 1);
            candies -= Math.min(candies, i + 1);
            i += 1;
        }
        return ans;
    }
}

[sol1-C++]

class Solution {
public:
    vector<int> distributeCandies(int candies, int num_people) {
        vector<int> ans(num_people,0);
        int i = 0;
        while (candies != 0) {
            ans[i % num_people] += min(candies, i + 1);
            candies -= min(candies, i + 1);
            ++i;
        }
        return ans;
    }
};

复杂度分析

• 时间复杂度：\mathcal{O}(max(\sqrt{G}, N))，G 为糖果数量，N 为人数。

  本方法的时间复杂度取决于循环到底走多少步。设总的步数为 s，用等差数列求和公式 可以求得 s 步时发放的糖果数量为 s(s+1)}{2。那么只要 s^2+s\geq 2G 糖果就可以保证被发完。

  而只要当 s\geq \sqrt{2G 时，就有 s^2\geq 2G，显然也有 s^2+s\geq 2G。

  因此可知总的步数 s\leq \left \lceil{\sqrt{2G} }\right \rceil，时间复杂度为 \mathcal{O}(\sqrt G)。

  另外建立糖果分配数组并初值赋值需要 \mathcal{O}(N) 的时间，因此总的时间复杂度为 \mathcal{O}(max(\sqrt{G}, N))。

• 空间复杂度：\mathcal{O}(1)，除了答案数组只需要常数空间来存储若干变量。

方法二：等差数列求和

思路

这是一个数学问题，可以对其简化。

更好的做法是使用一个简单的公式代表糖果分配，可以在 \mathcal{O}(N) 时间内完成糖果分发，并生成最终的分配数组。

接下来逐步推导该公式。

获得完整礼物的人数

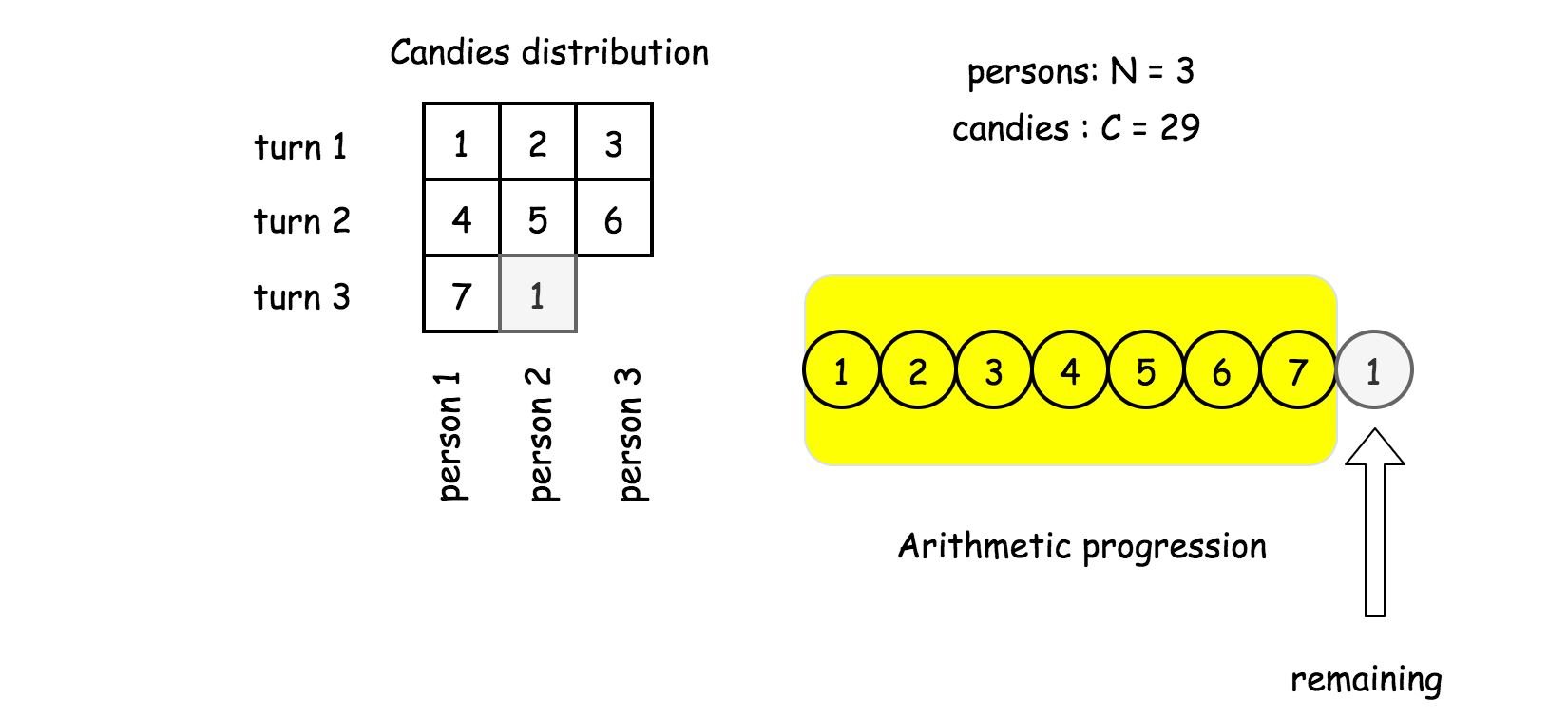
除了最后一份礼物数量由剩余糖果数量决定以外，其他礼物的数量都是从 1 开始构成的等差数列。

{:width=480}

假设数列一共有 p 个元素，剩余的糖果就是糖果数量 C 与等差数列前 p 项之差。

\textrm{remaining} = C - \sum\limits_{k = 0}^{k = p}{k}

等差数列求和公式是中学知识 ，剩余糖果数量可以表示为：

\textrm{remaining} = C - p(p + 1)}{2}

剩余糖果数量大于等于 0，小于下一份礼物数量 p + 1。

0 \le C - p(p + 1)}{2} < p + 1

化简上式得

\sqrt{2C + 1/4} } - 3/2} < p \le \sqrt{2C + 1/4} } - 1/2}

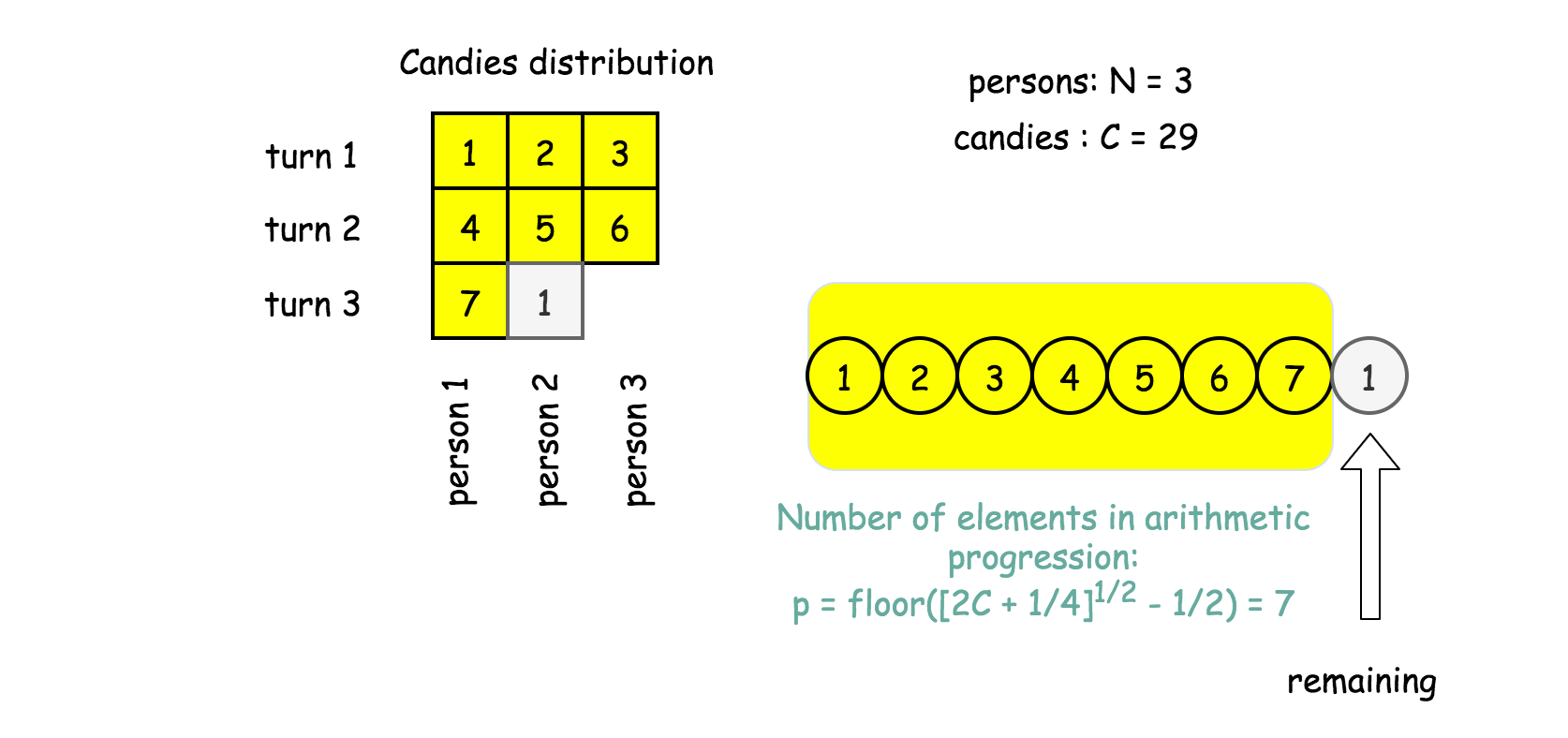
该区间内只有一个整数，因此可以知道等差数列的元素数量

p = \textrm{floor}\left(\sqrt{2C + 1/4} } - 1/2}\right)

{:width=480}

完整分发礼物的回合

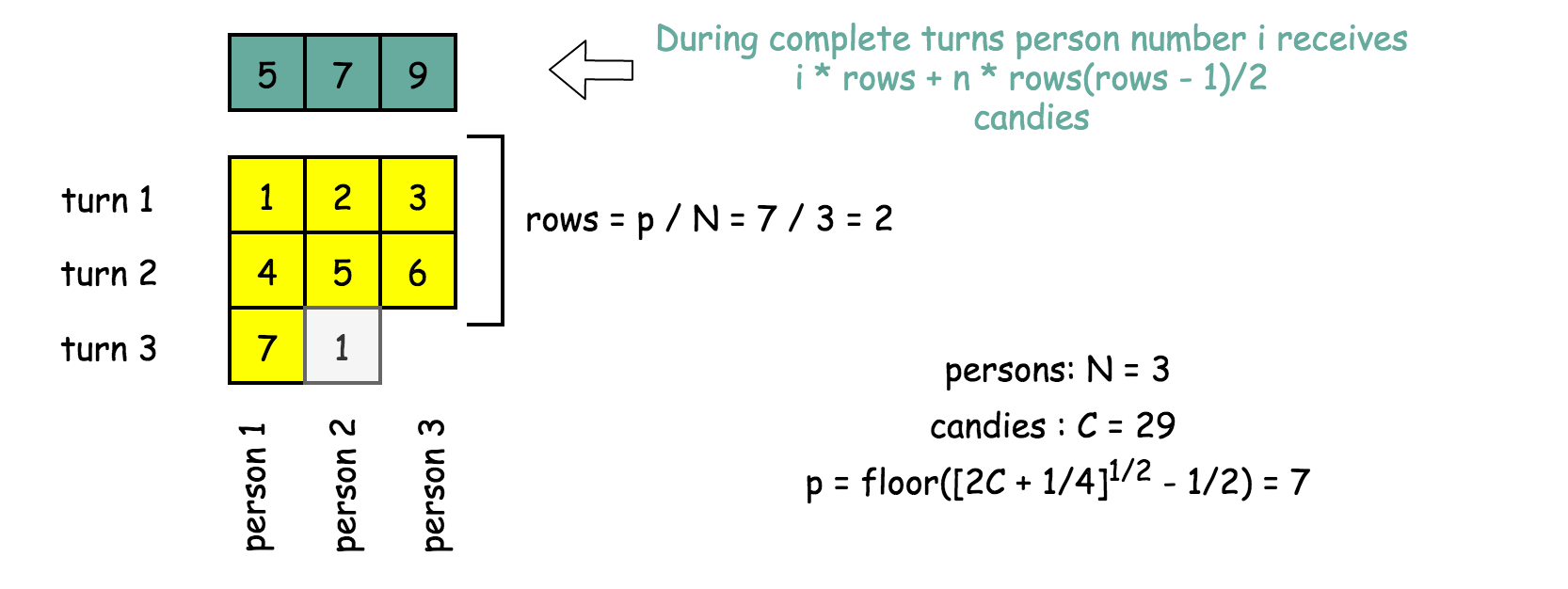
一个回合表示给每个人都分发一份完整的礼物。将 p 份完整的礼物分发给 N 个人，共可以分发的回合数：rows = p / N。

在 rows 个完整回合中，第 i 个人获得礼物：

d[i] = i + (i + N) + (i + 2N) + … (i + (\textrm{rows} - 1) N) =
i \times \textrm{rows} + N \textrm{rows}(\textrm{rows} - 1)}{2}

{:width=480}

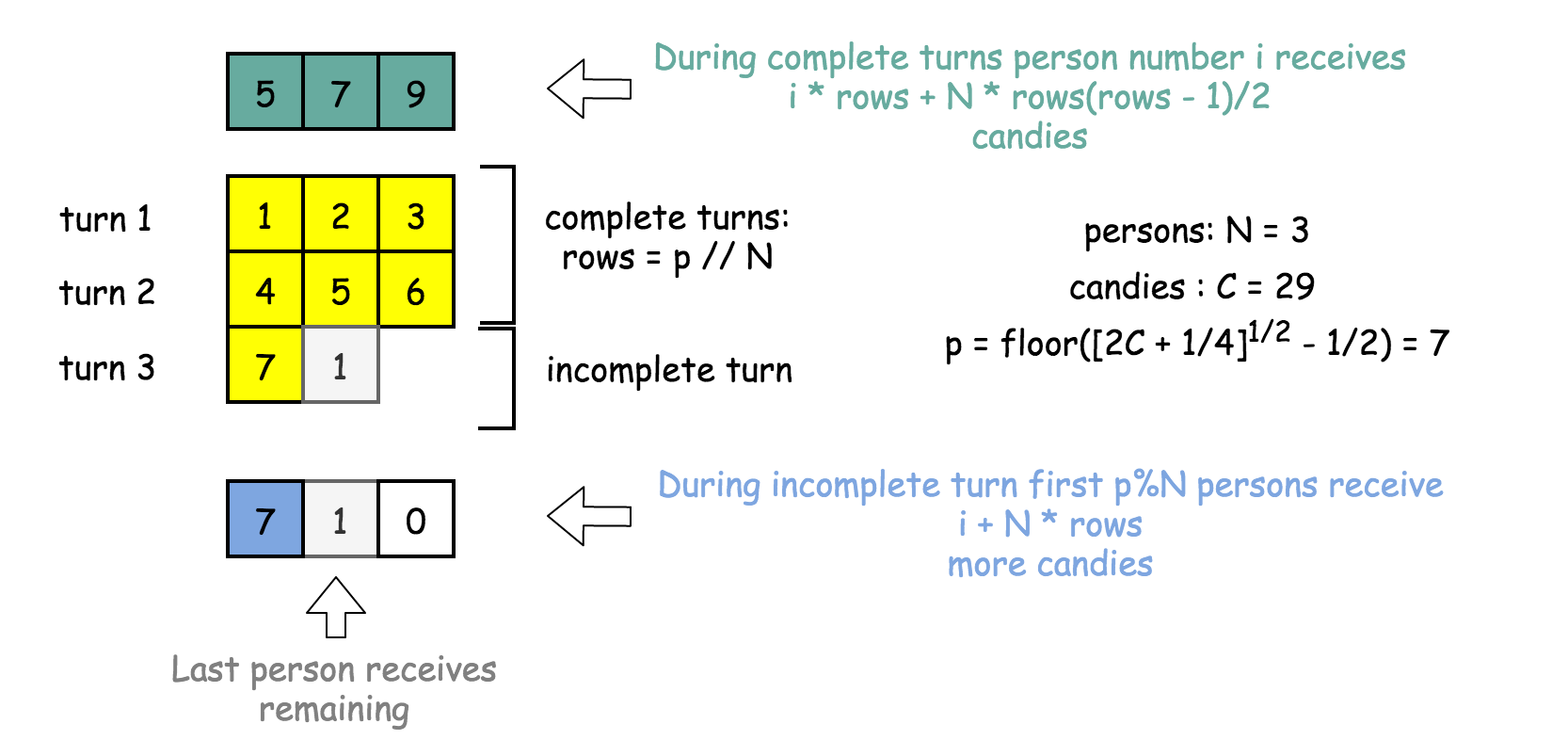
不完整分发礼物的回合

最后一个回合可能不完整，因为有可能只是一部分人收到了礼物。

在最后一个回合中，可以计算出收到完整礼物的人数 cols = p % N。这些人比其他人多获得一份完整的礼物。

d[i] += i + N \times \textrm{rows}

最后一位拥有礼物的人获得所有剩余的糖果。

d[\textrm{cols} + 1] += \textrm{remaining}

{:width=480}

这就是分发所有糖果的过程。

算法

• 计算完整礼物的份数

  p = \textrm{floor}\left(\sqrt{2C + 1/4} } - 1/2}\right)

  最后一份礼物的糖果数量

  \textrm{remaining} = C - p(p + 1)}{2}

• 完整的分发回合数：rows = p // n。此时每个人拥有的礼物数量：

  d[i] = i \times \textrm{rows} + N \textrm{rows}(\textrm{rows} - 1)}{2}

• 前 p % N 个人最后再获得一份完整的礼物：d[i] += i + N \times \textrm{rows。

• 将剩余的糖果分发给第 p % N 个后面的一个人。

• 返回糖果分配数组：d。

[sol2-Python3]

class Solution:
    def distributeCandies(self, candies: int, num_people: int) -> List[int]:
        n = num_people
        # how many people received complete gifts
        p = int((2 * candies + 0.25)**0.5 - 0.5) 
        remaining = int(candies - (p + 1) * p * 0.5)
        rows, cols = p // n, p % n
        
        d = [0] * n
        for i in range(n):
            # complete rows
            d[i] = (i + 1) * rows + int(rows * (rows - 1) * 0.5) * n
            # cols in the last row
            if i < cols:
                d[i] += i + 1 + rows * n
        # remaining candies        
        d[cols] += remaining
        return d

[sol2-Java]

class Solution {
    public int[] distributeCandies(int candies, int num_people) {
        int n = num_people;
        // how many people received complete gifts
        int p = (int) (Math.sqrt(2 * candies + 0.25) - 0.5);
        int remaining = (int)(candies - (p + 1) * p * 0.5);
        int rows = p / n, cols = p % n;

        int[] d = new int[n];
        for (int i = 0; i < n; ++i) {
            // complete rows
            d[i] = (i + 1) * rows + (int)(rows * (rows - 1) * 0.5) * n;
            // cols in the last row
            if (i < cols) {
                d[i] += i + 1 + rows * n;
            }
        }
        // remaining candies        
        d[cols] += remaining;
        return d;
    }
}

[sol2-C++]

class Solution {
public:
    vector<int> distributeCandies(int candies, int num_people) {
        int n = num_people;
        // how many people received complete gifts
        int p = (int)(sqrt(2 * candies + 0.25) - 0.5);
        int remaining = (int)(candies - (p + 1) * p * 0.5);
        int rows = p / n, cols = p % n;

        vector<int> d(n, 0);
        for (int i = 0; i < n; ++i) {
            // complete rows
            d[i] = (i + 1) * rows + (int)(rows * (rows - 1) * 0.5) * n;
            // cols in the last row
            if (i < cols) d[i] += i + 1 + rows * n;
        }
        // remaining candies 
        d[cols] += remaining;
        return d;
    }
};

复杂度分析

• 时间复杂度：\mathcal{O}(N)，计算 N 个人的糖果数量。

• 空间复杂度：\mathcal{O}(1)，，除了答案数组只需要常数空间来存储若干变量。