1104-二叉树寻路

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 17:01:06 2023-09-13 17:01:06 Updated    

在一棵无限的二叉树上，每个节点都有两个子节点，树中的节点 逐行 依次按 “之” 字形进行标记。

如下图所示，在奇数行（即，第一行、第三行、第五行……）中，按从左到右的顺序进行标记；

而偶数行（即，第二行、第四行、第六行……）中，按从右到左的顺序进行标记。

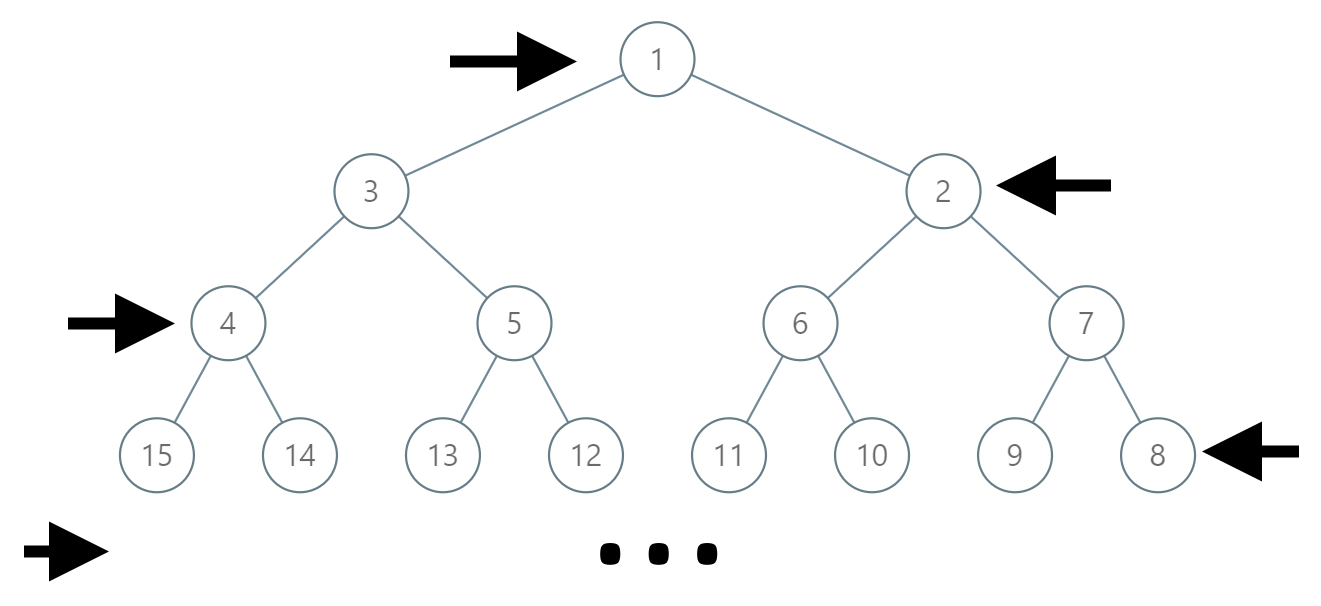
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2019/06/28/tree.png)

给你树上某一个节点的标号 label，请你返回从根节点到该标号为 label 节点的路径，该路径是由途经的节点标号所组成的。

示例 1：

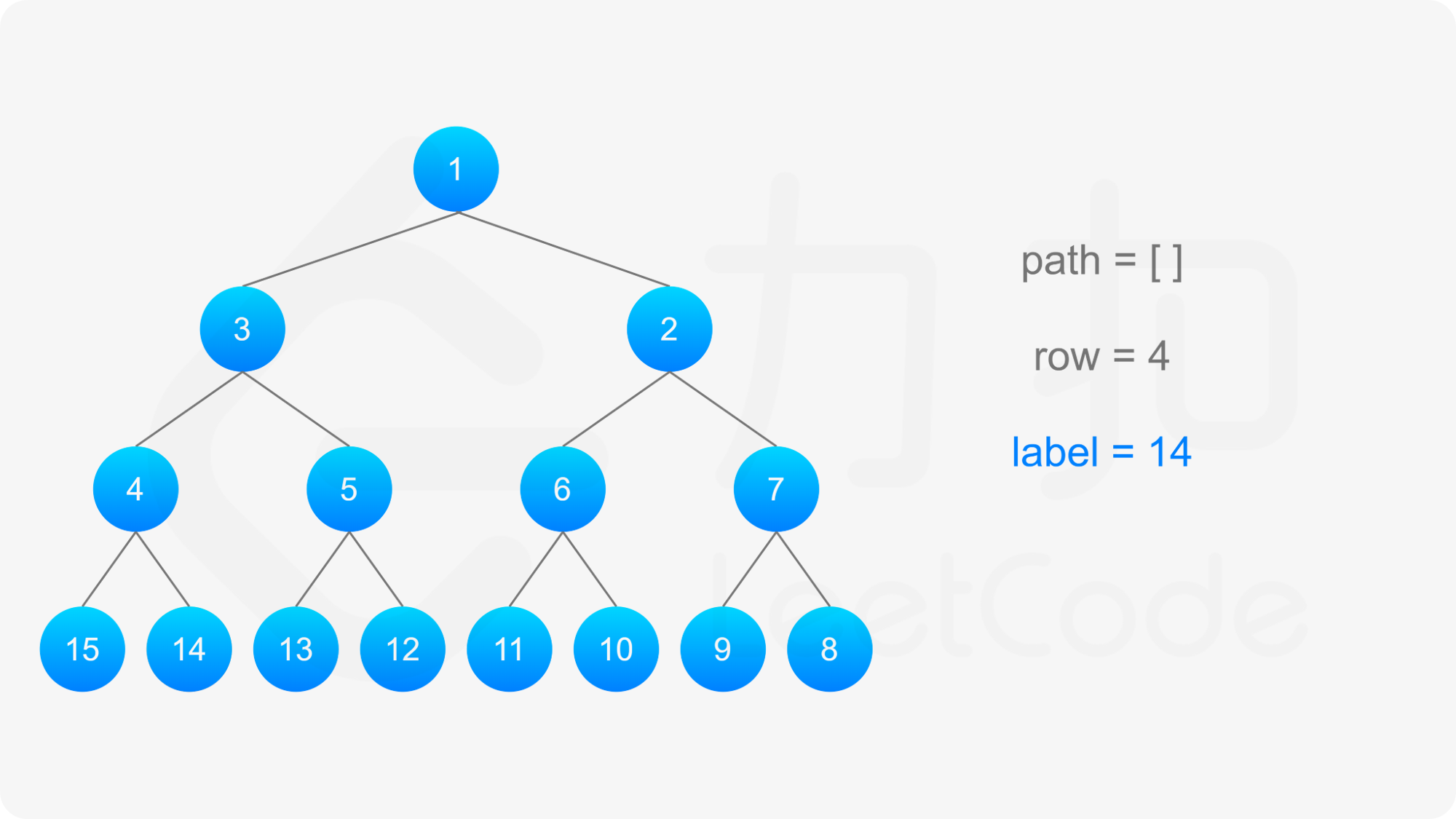
**输入：** label = 14
**输出：** [1,3,4,14]

示例 2：

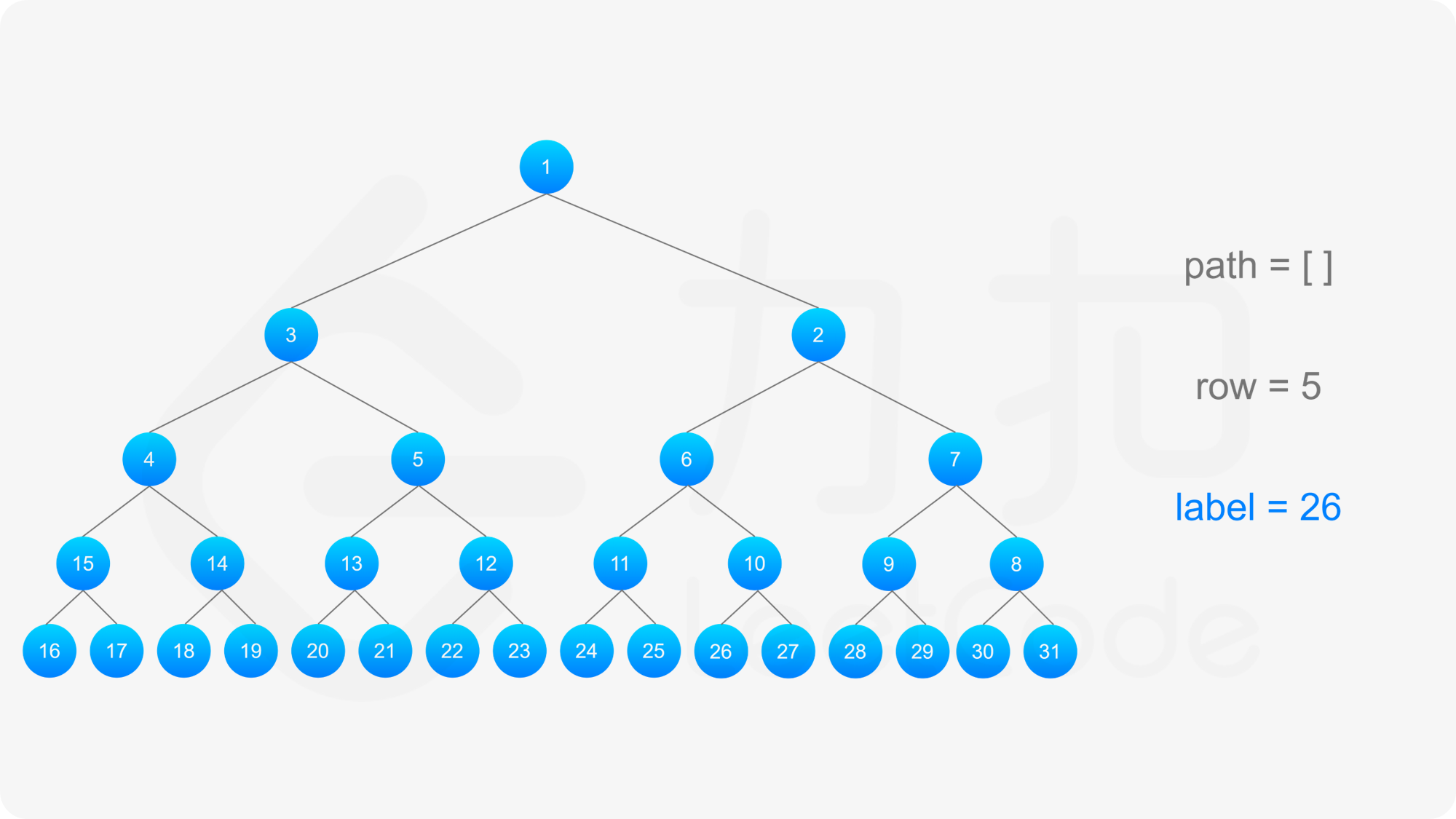
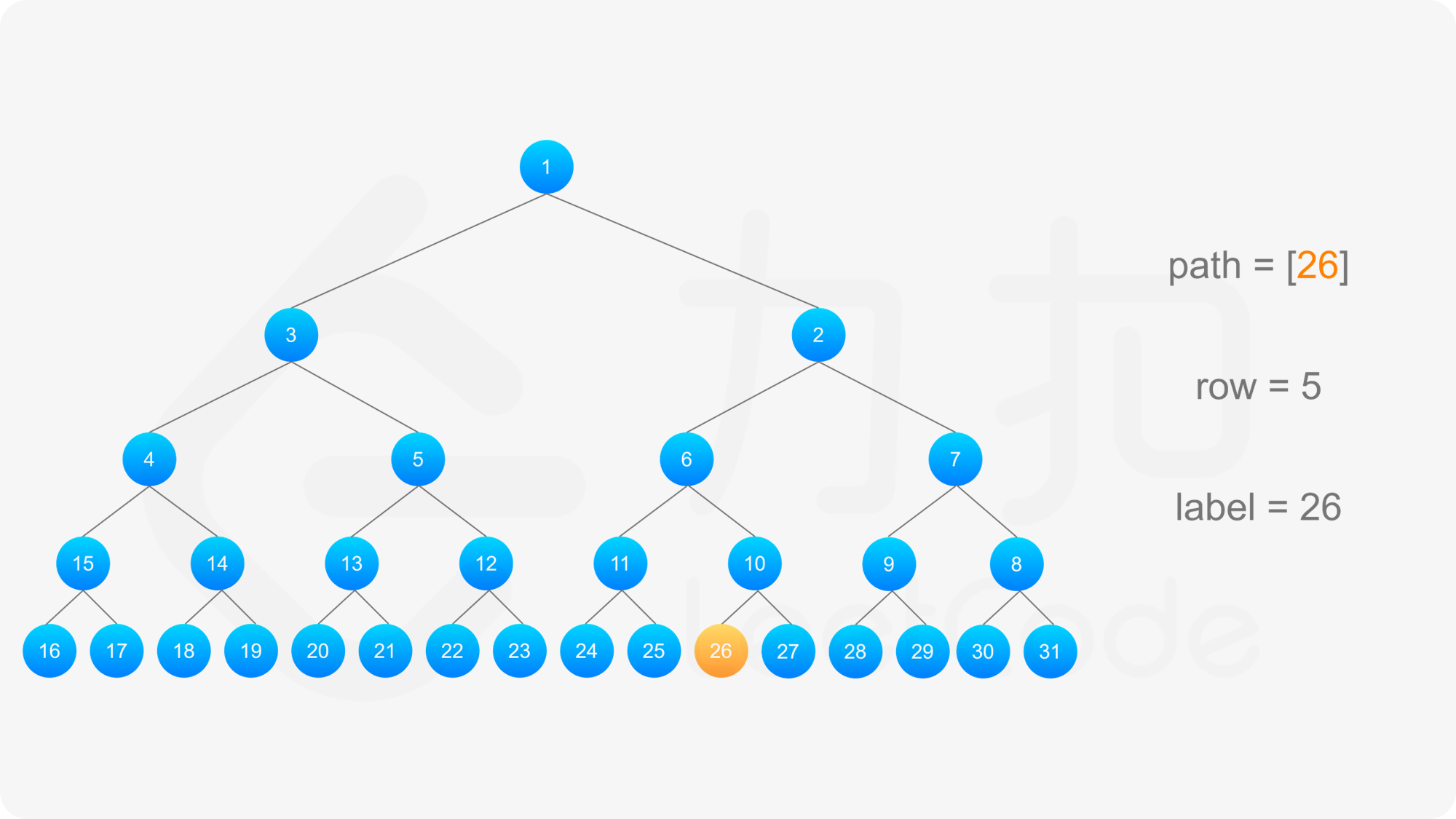
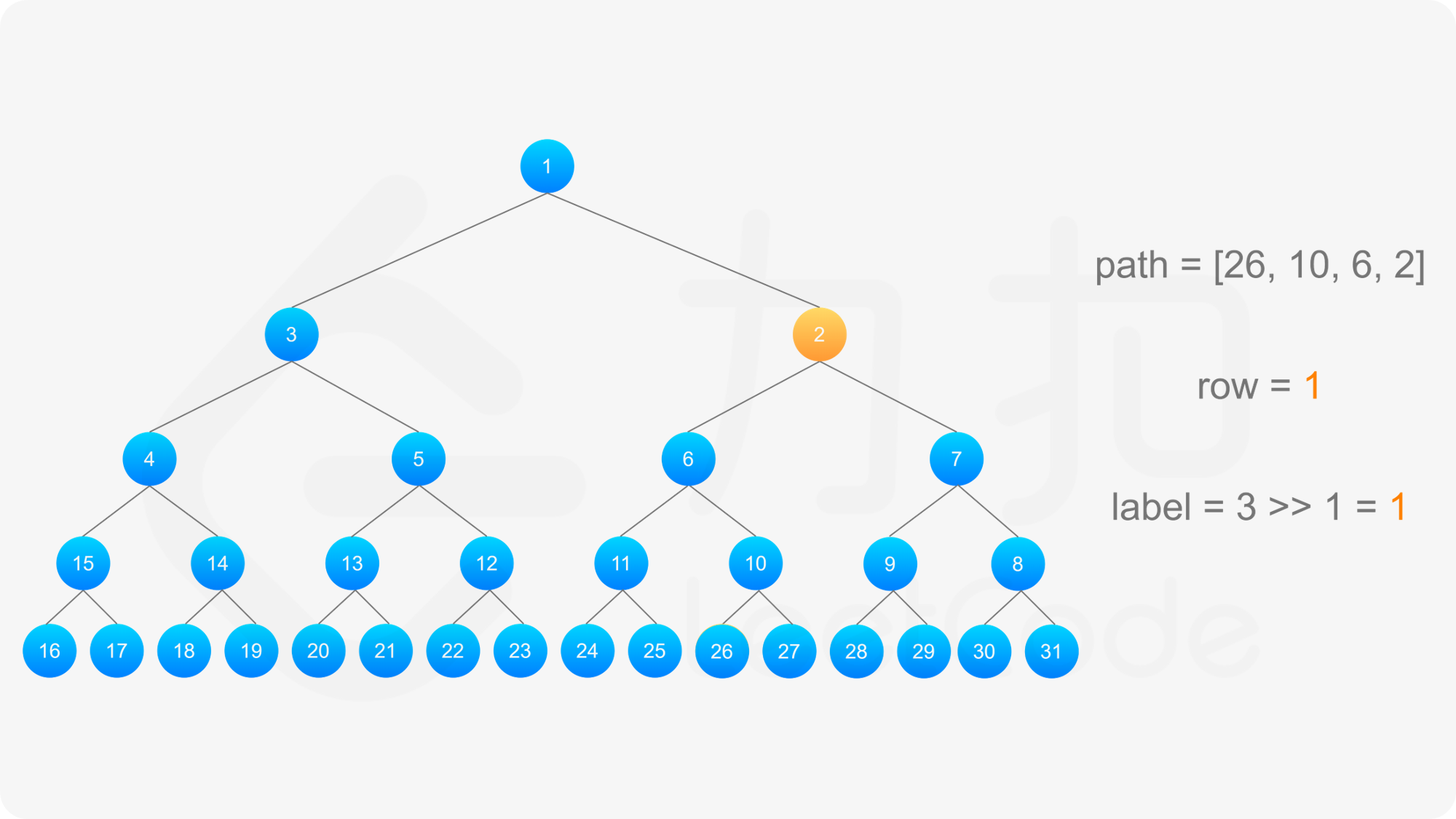
**输入：** label = 26
**输出：** [1,2,6,10,26]

提示：

  • 1 <= label <= 10^6

方法一：数学

我们先来研究一个简单的情形：二叉树的每一行都是按从左到右的顺序进行标记。此时二叉树满足以下性质：

  • 根节点位于第 1 行；

  • 第 i 行有 2^{i-1 个节点，最左边的节点标号为 2^{i-1，最右边的节点标号为 2^i-1；

  • 对于标号为 val 的节点，其左子节点的标号为 2 \times \textit{val，右子节点的标号为 2 \times \textit{val} + 1，当 val}>1 时，其父节点的标号为 \lfloor \textit{val} }{2} \rfloor。

对于给定节点的标号 label，可以根据上述性质得到从该节点到根节点的路径，将路径反转后，即为从根节点到标号 label 的节点的路径。

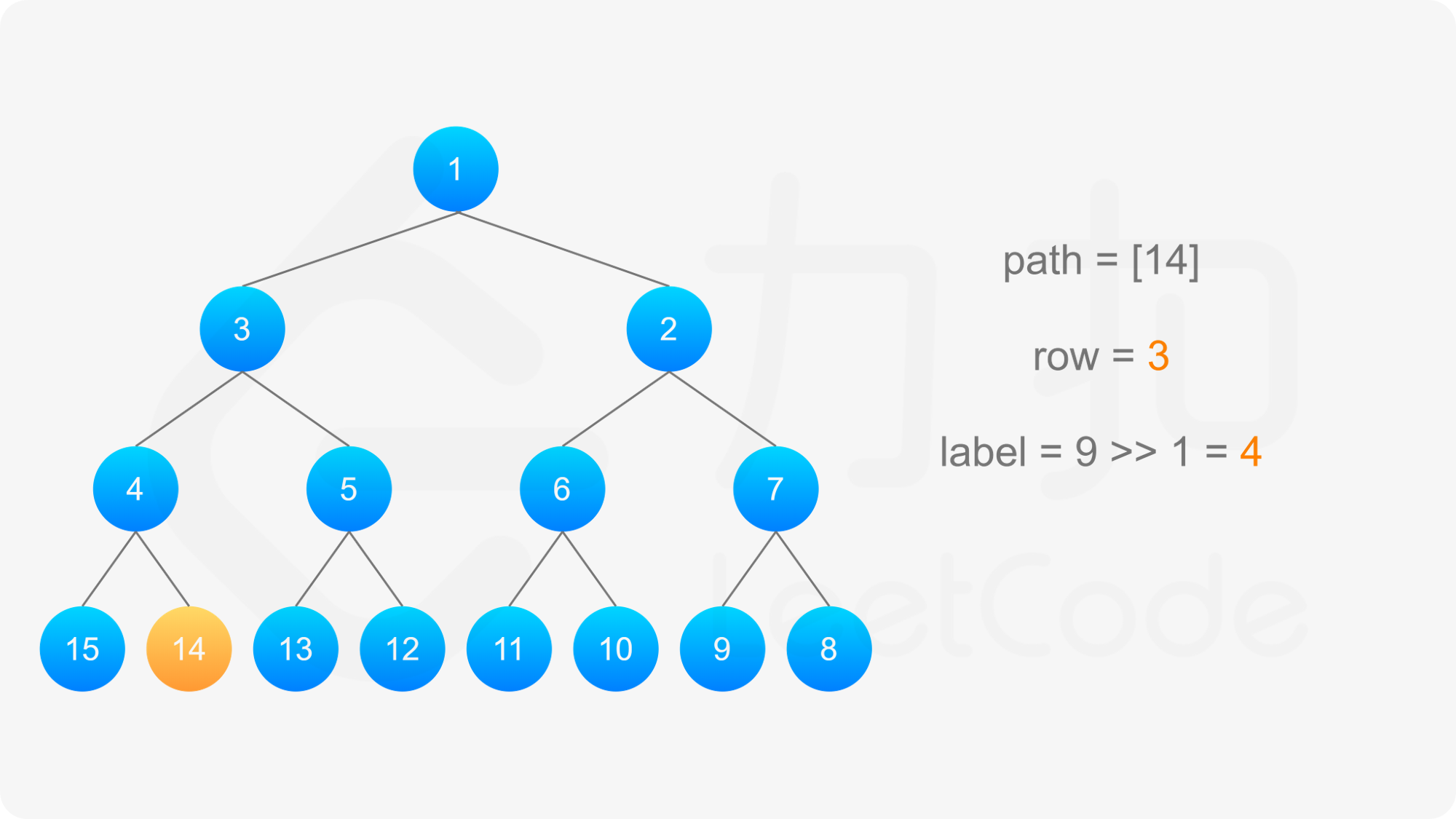
回到这题，对于偶数行按从右到左的顺序进行标记的情况，可以转换成按从左到右的顺序进行标记的情况，然后按照上述思路得到路径，只要对偶数行的标号进行转换即可。为了表述简洁，下文将按从左到右的顺序进行标记时的节点的标号称为「从左到右标号」。

首先找到标号为 label 的节点所在的行和该节点的「从左到右标号」。为了找到节点所在行，需要找到 i 满足 2^{i-1} \le \textit{label} < 2^i，则该节点在第 i 行。该节点的「从左到右标号」需要根据 i 的奇偶性计算：

  • 当 i 是奇数时，第 i 行为按从左到右的顺序进行标记，因此该节点的「从左到右标号」即为 label；

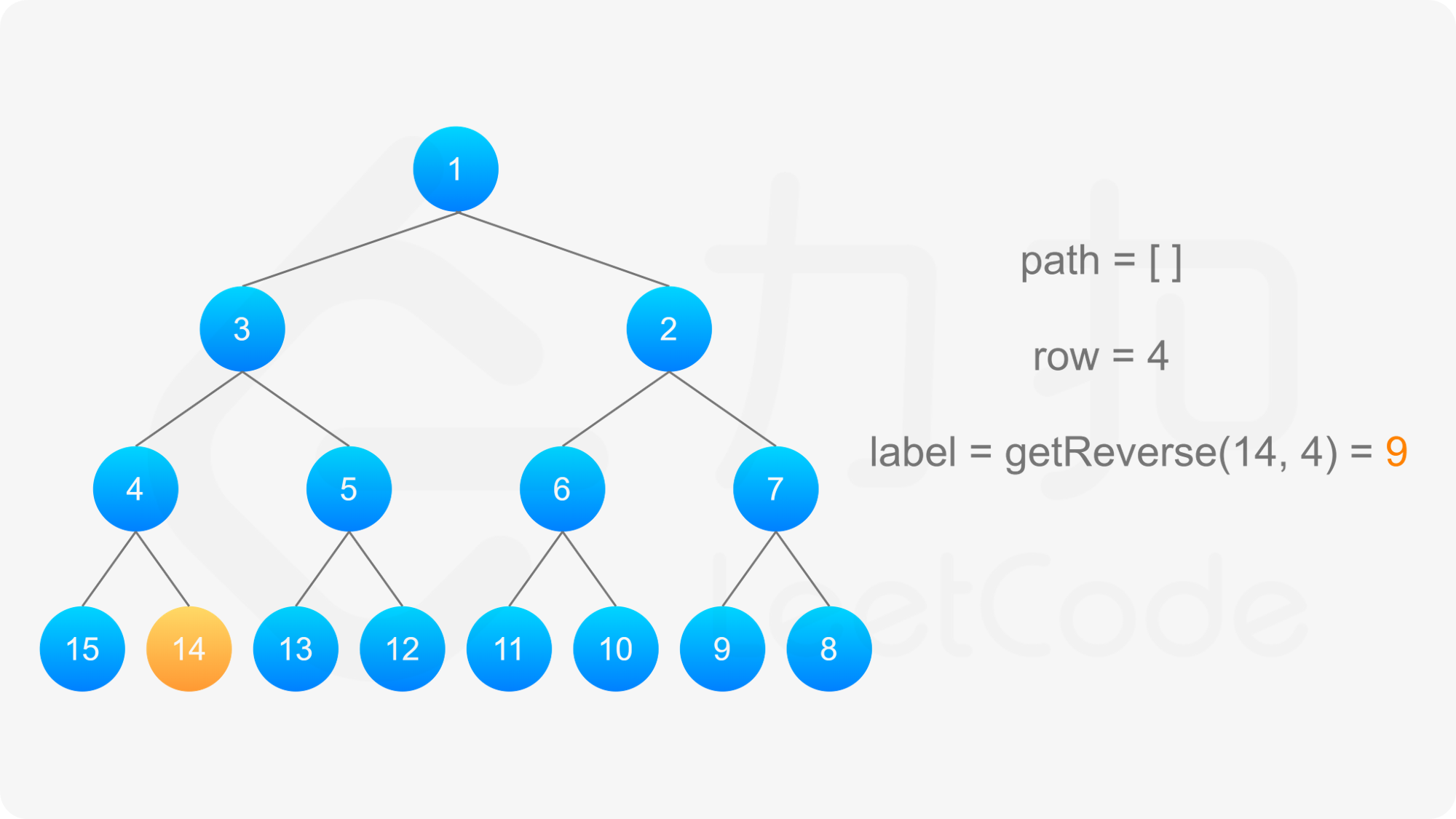
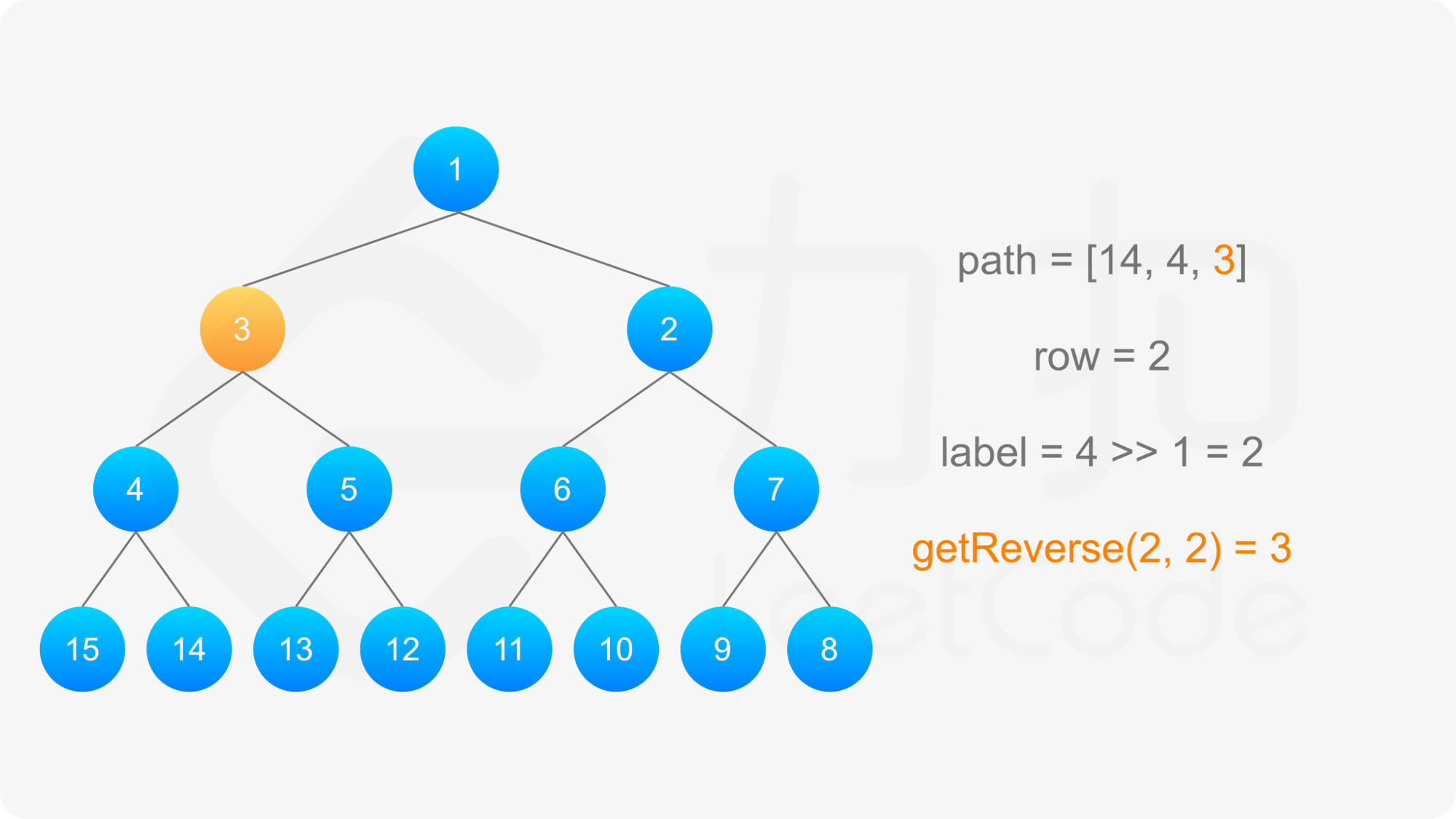
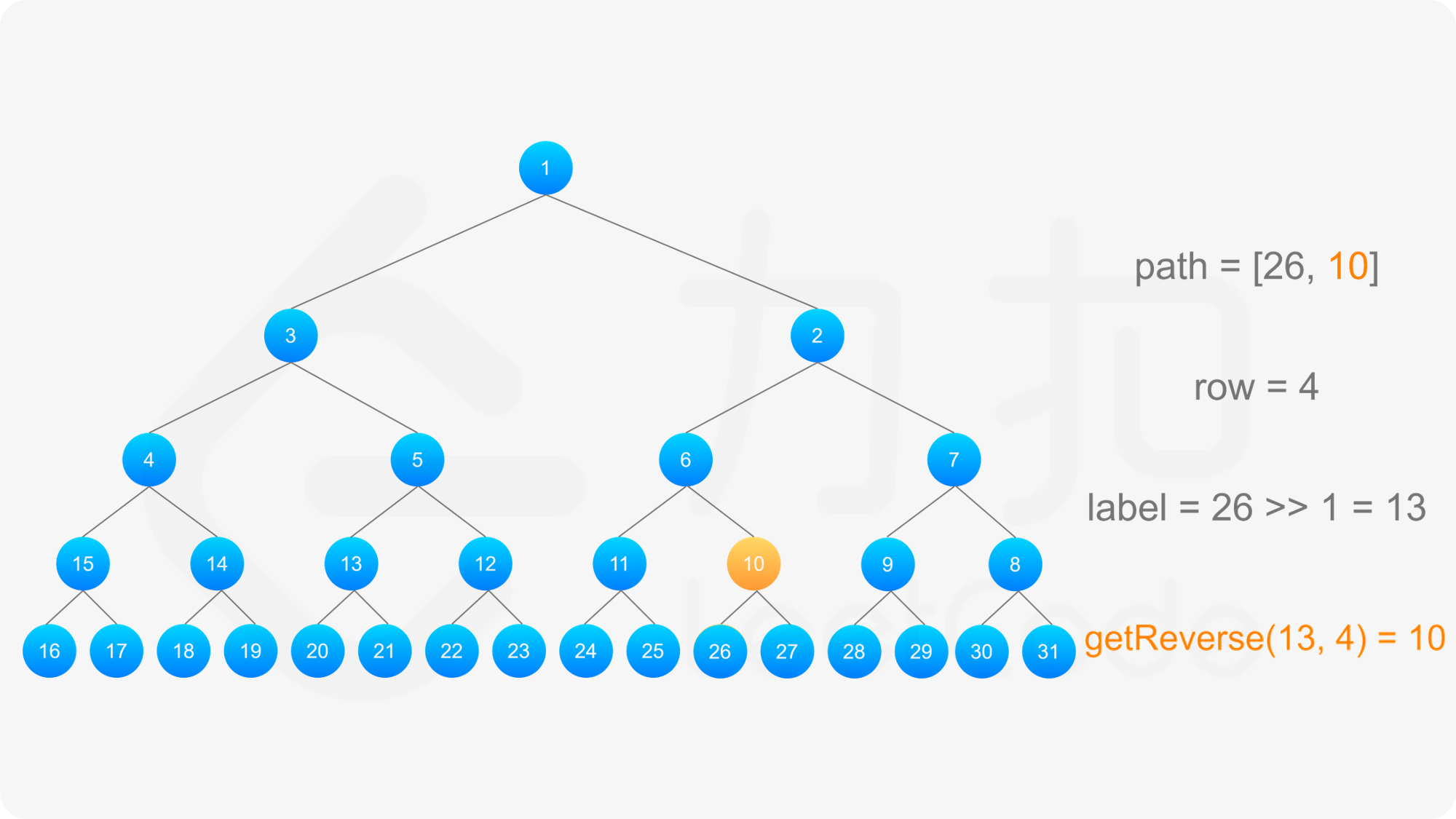
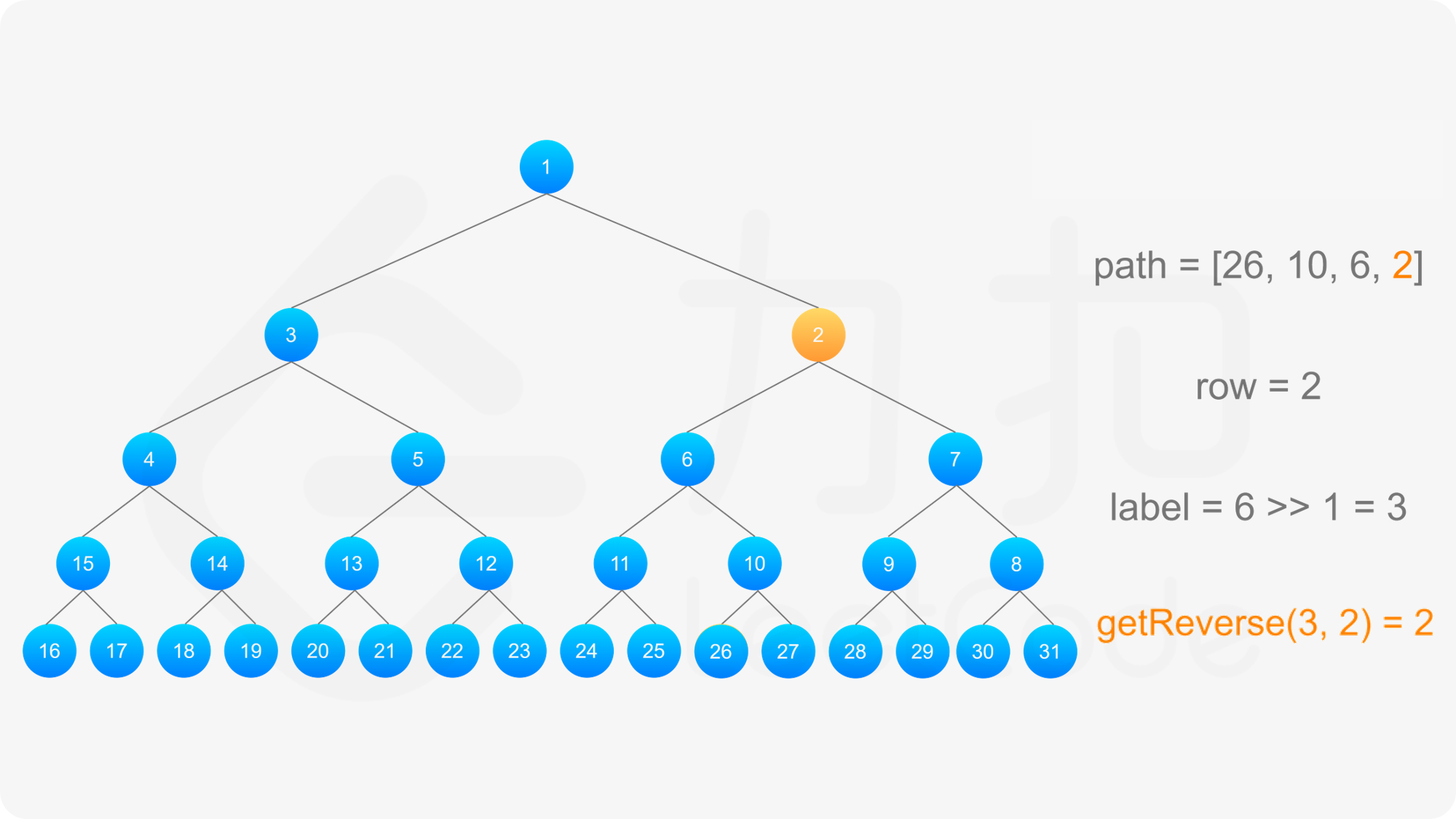
  • 当 i 是偶数时，第 i 行为按从右到左的顺序进行标记，将整行的标号左右翻转之后得到按从左到右的顺序进行标记的标号，对于同一个节点，其翻转前后的标号之和为 2^{i-1} + 2^i - 1，因此标号为 label 的节点的「从左到右标号」为 2^{i-1} + 2^i - 1 - \textit{label。

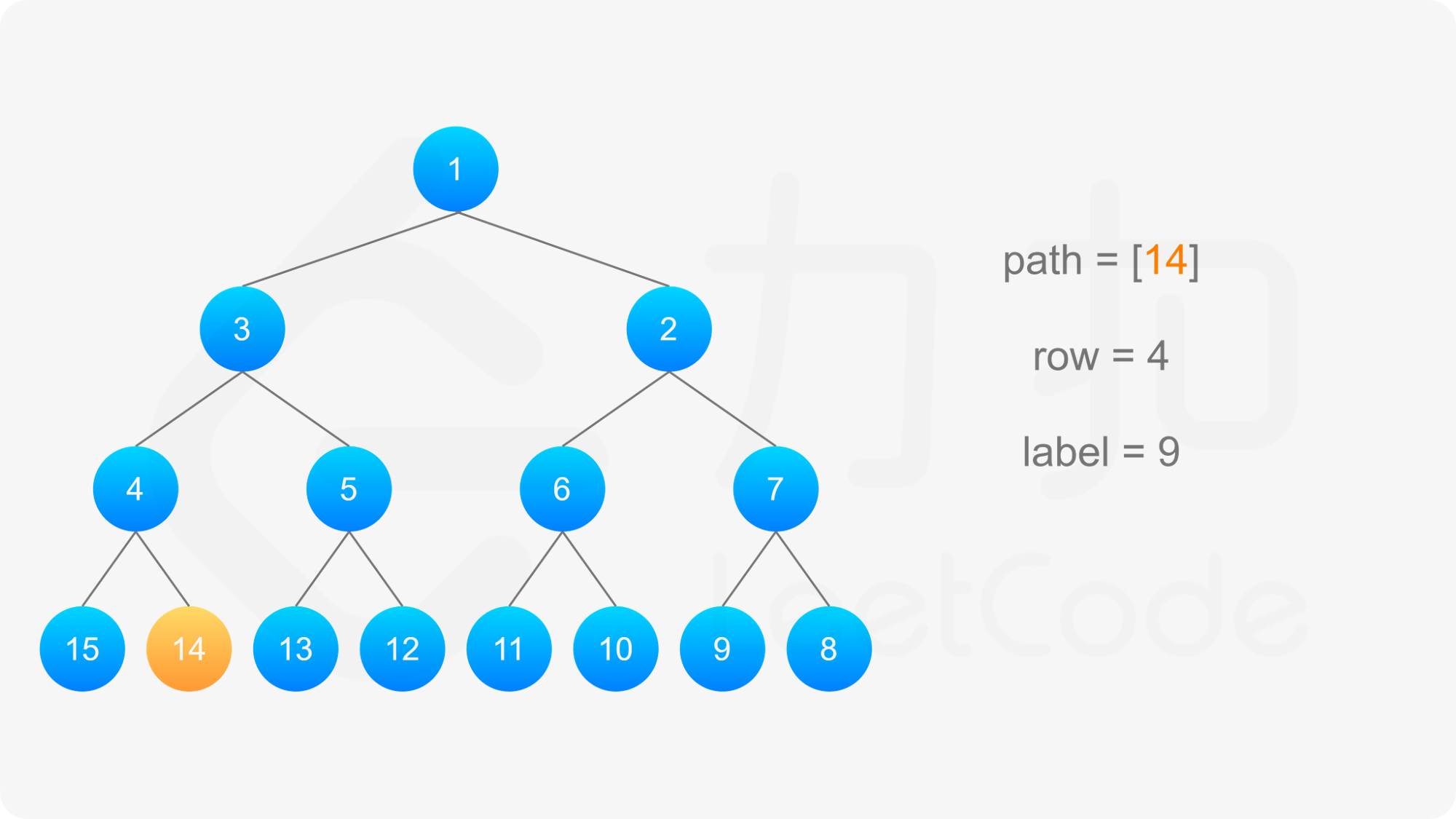
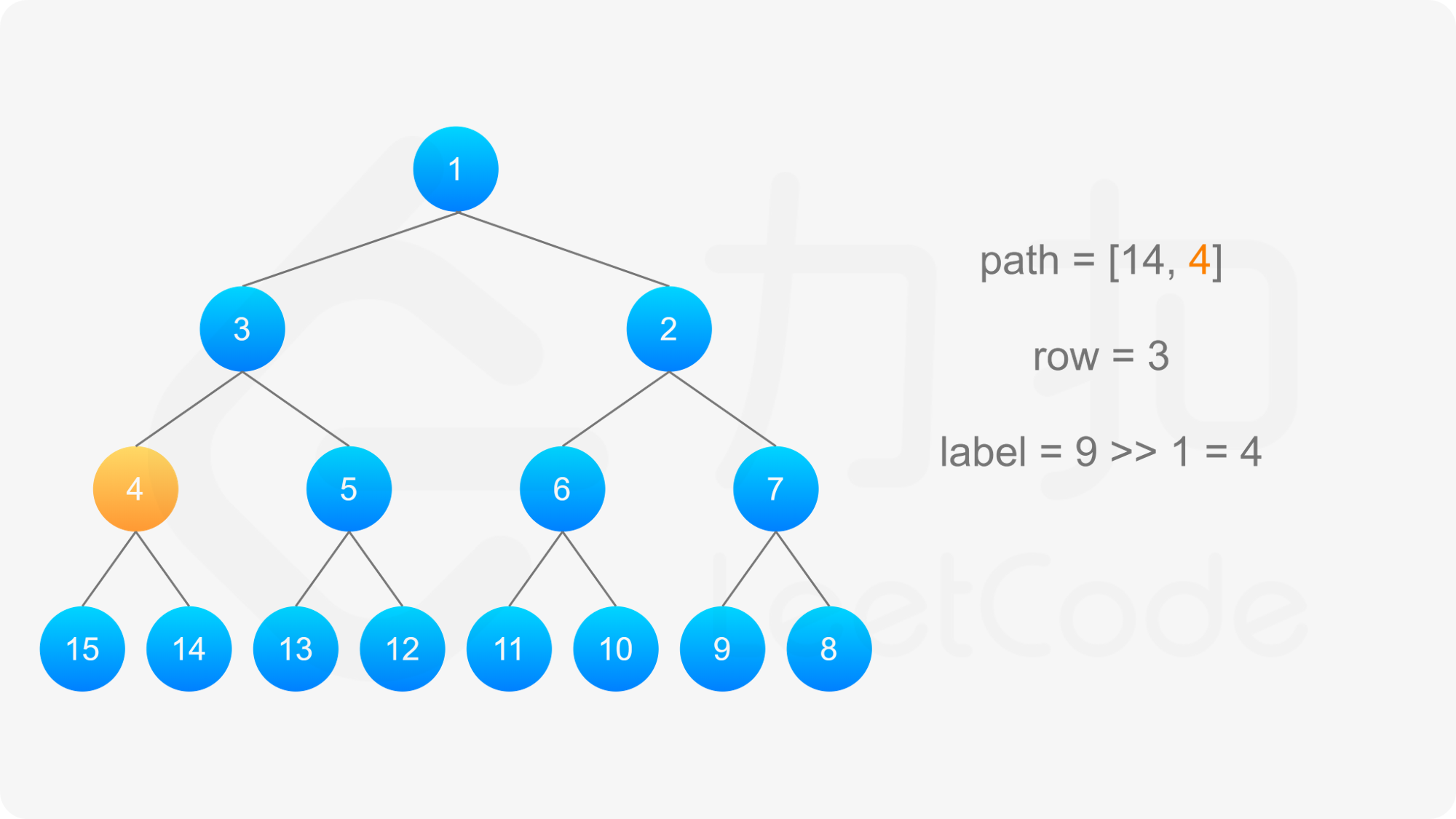
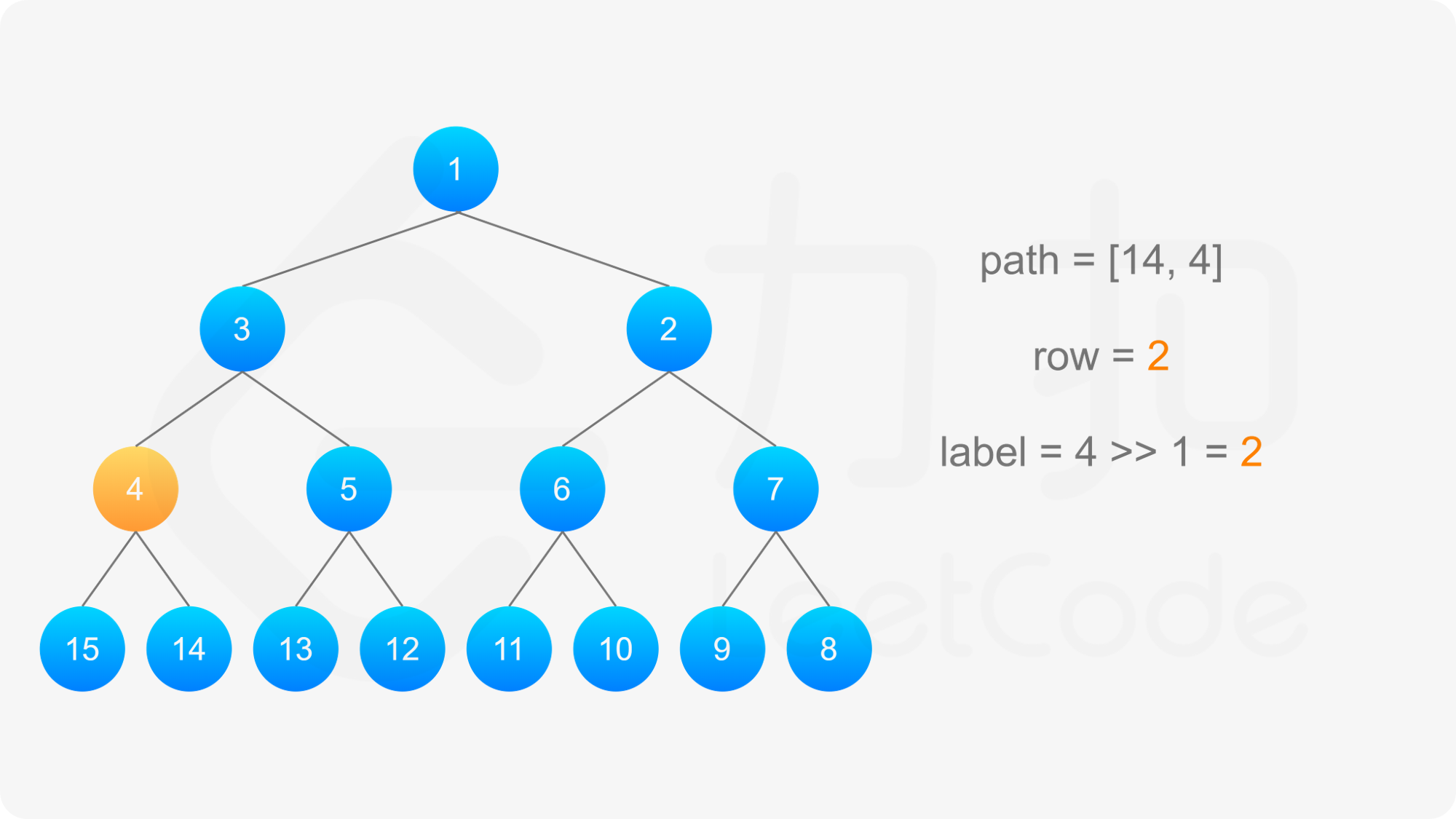
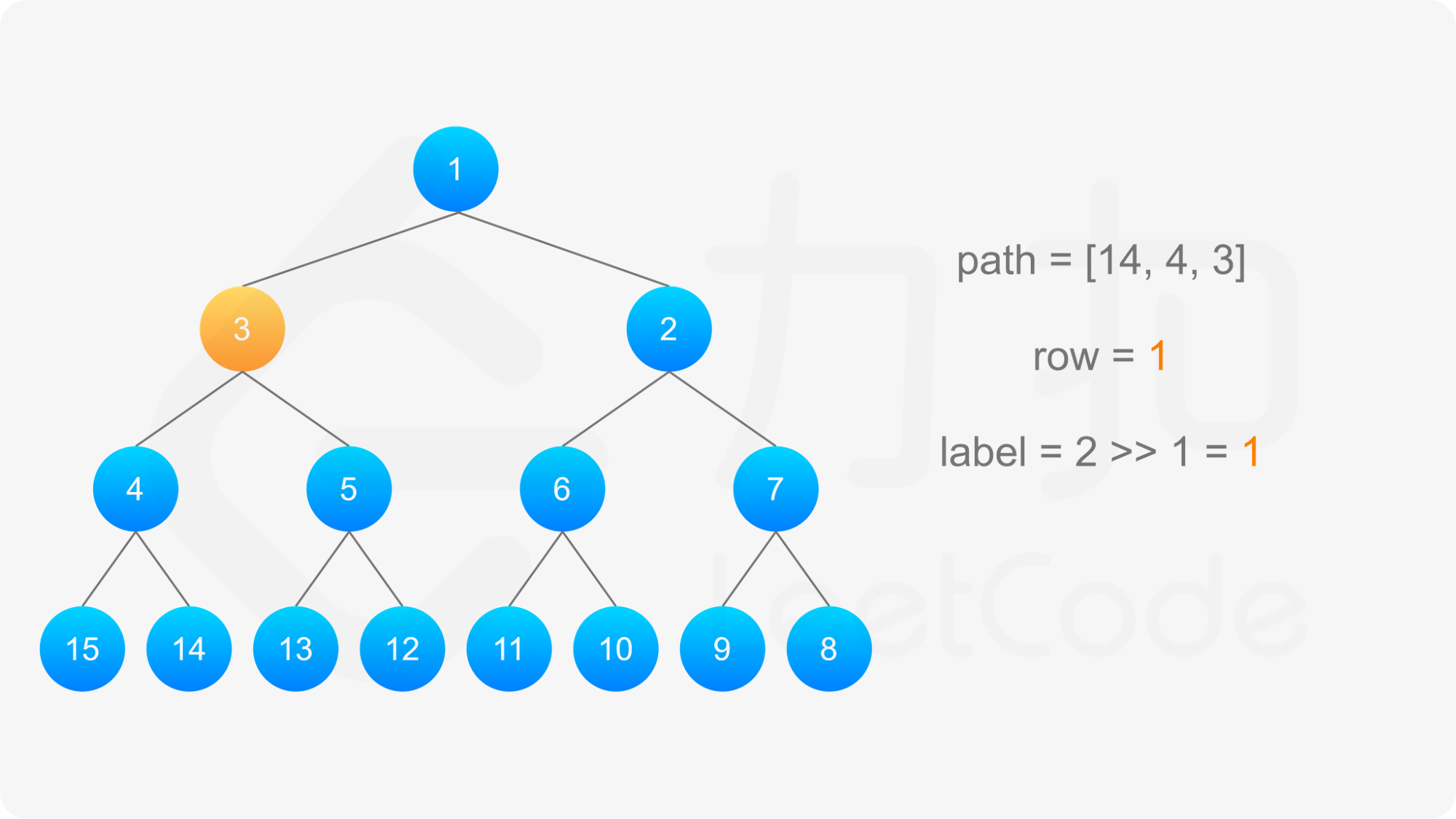
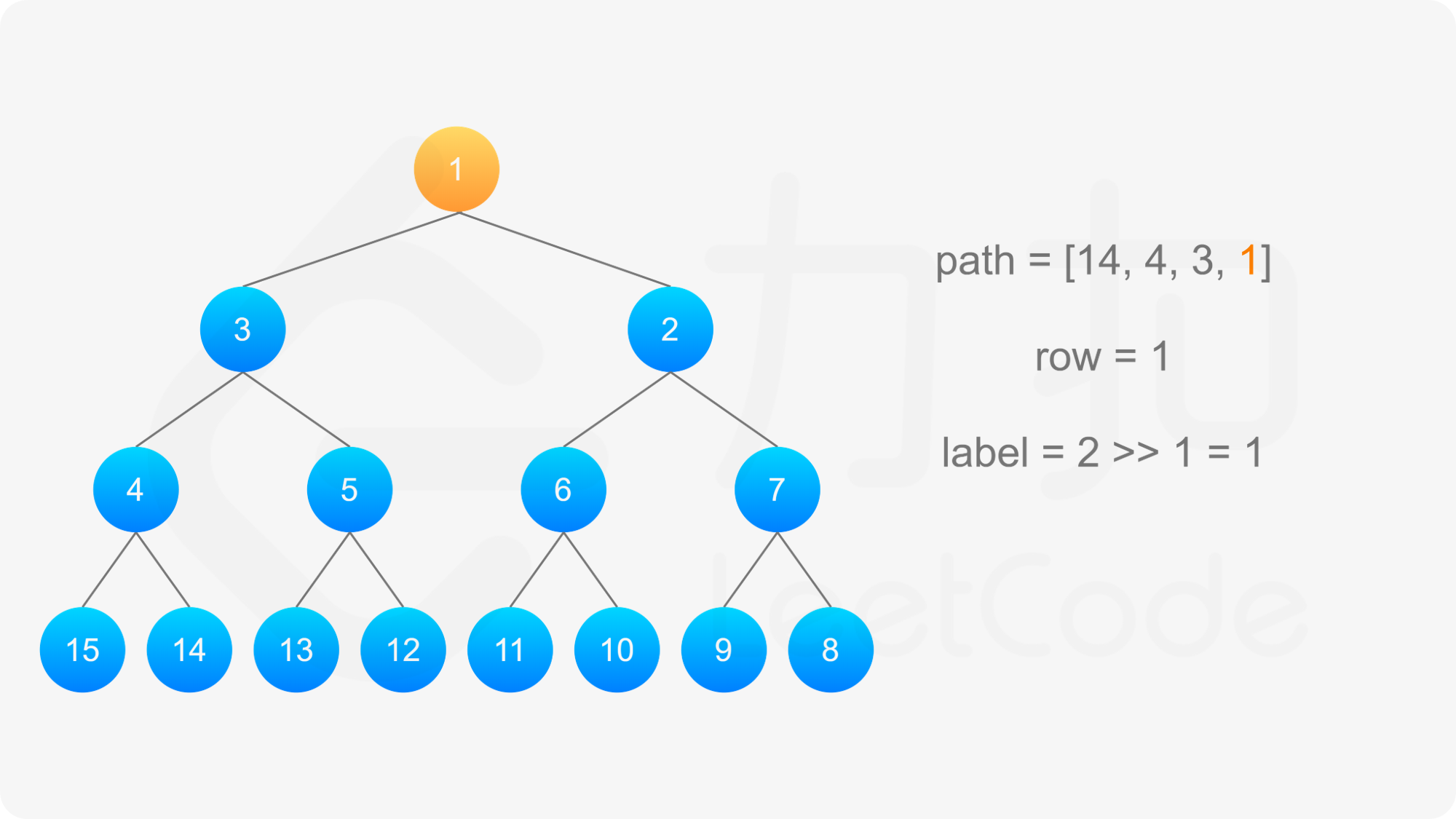
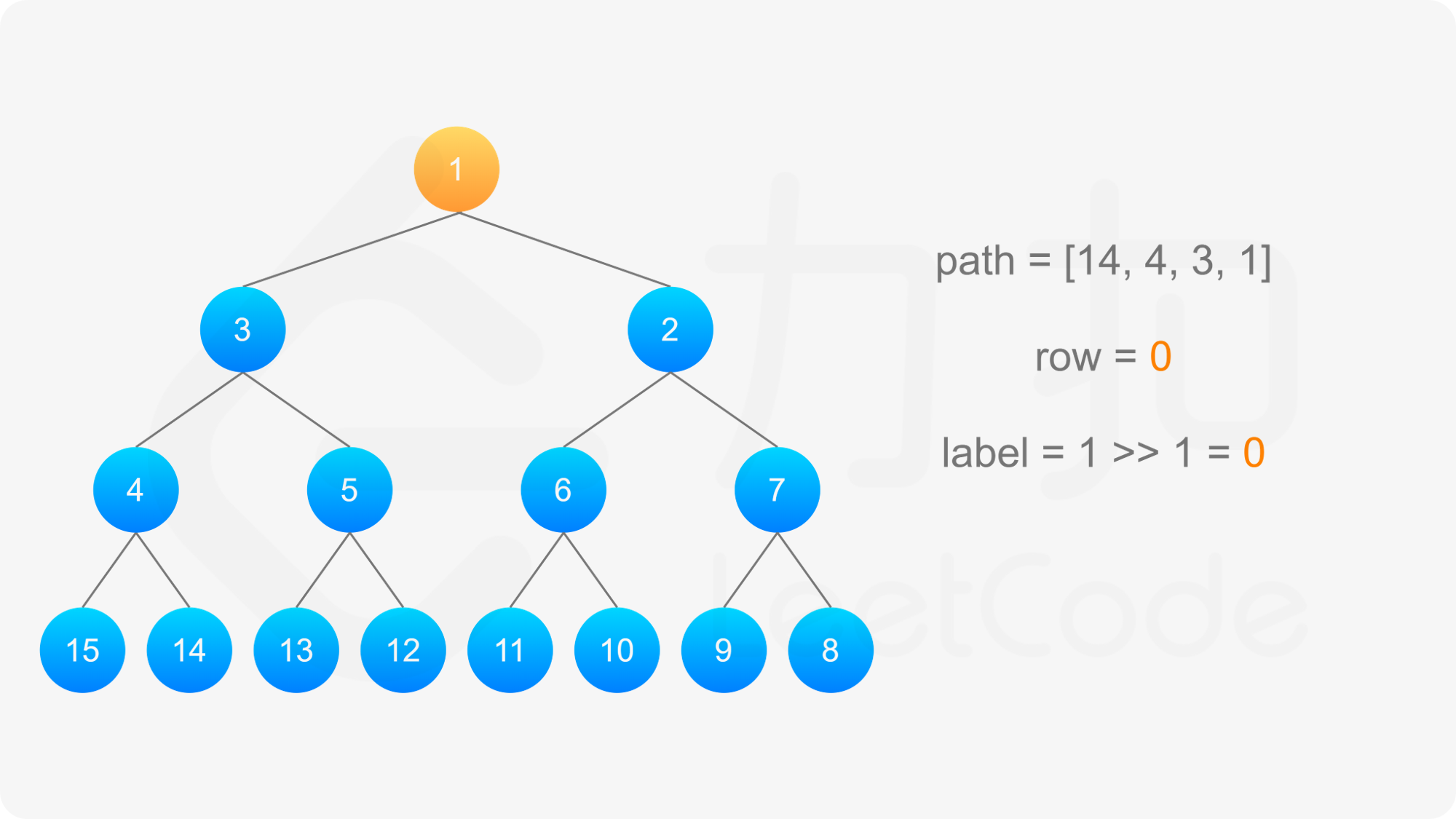
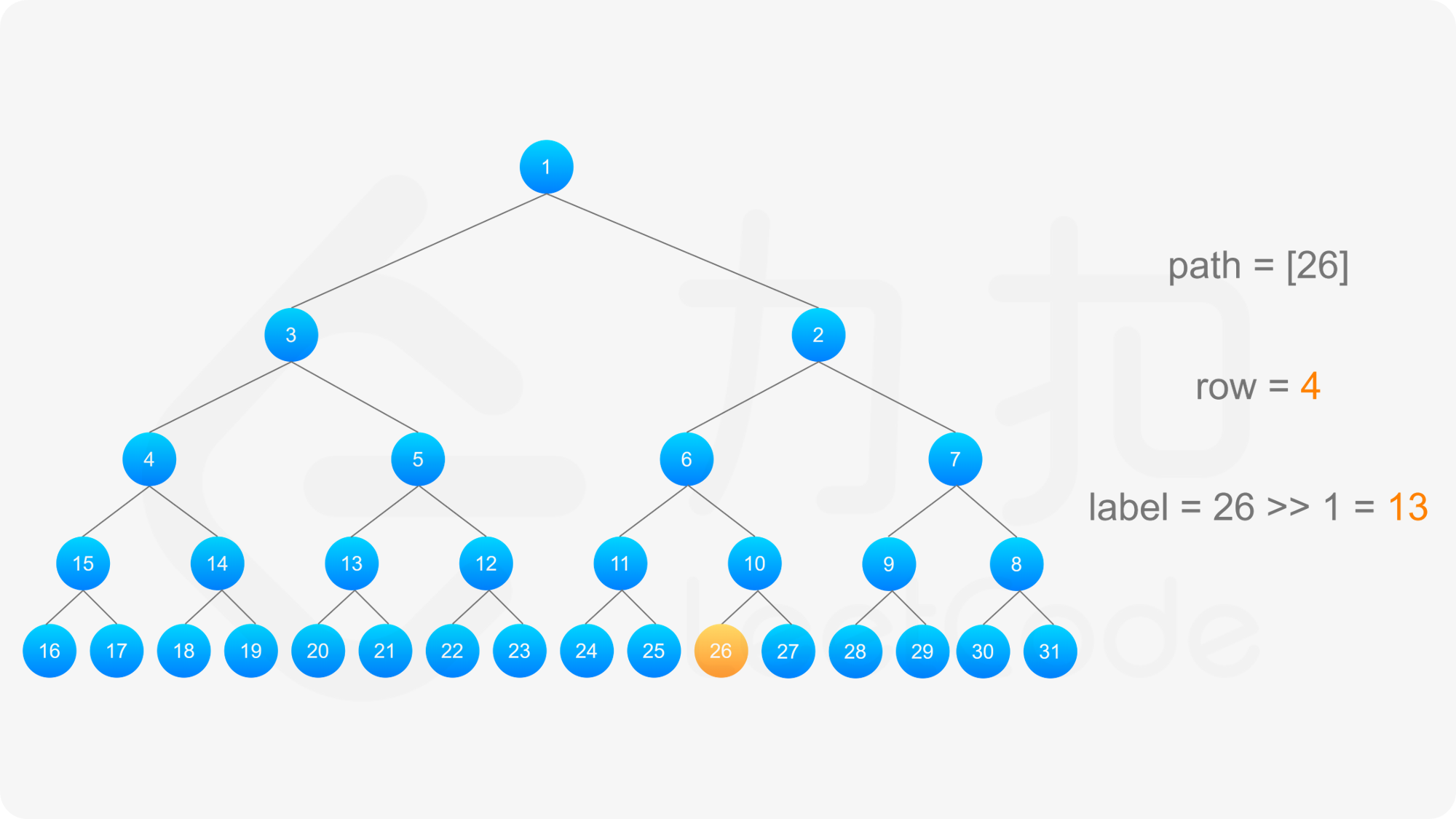
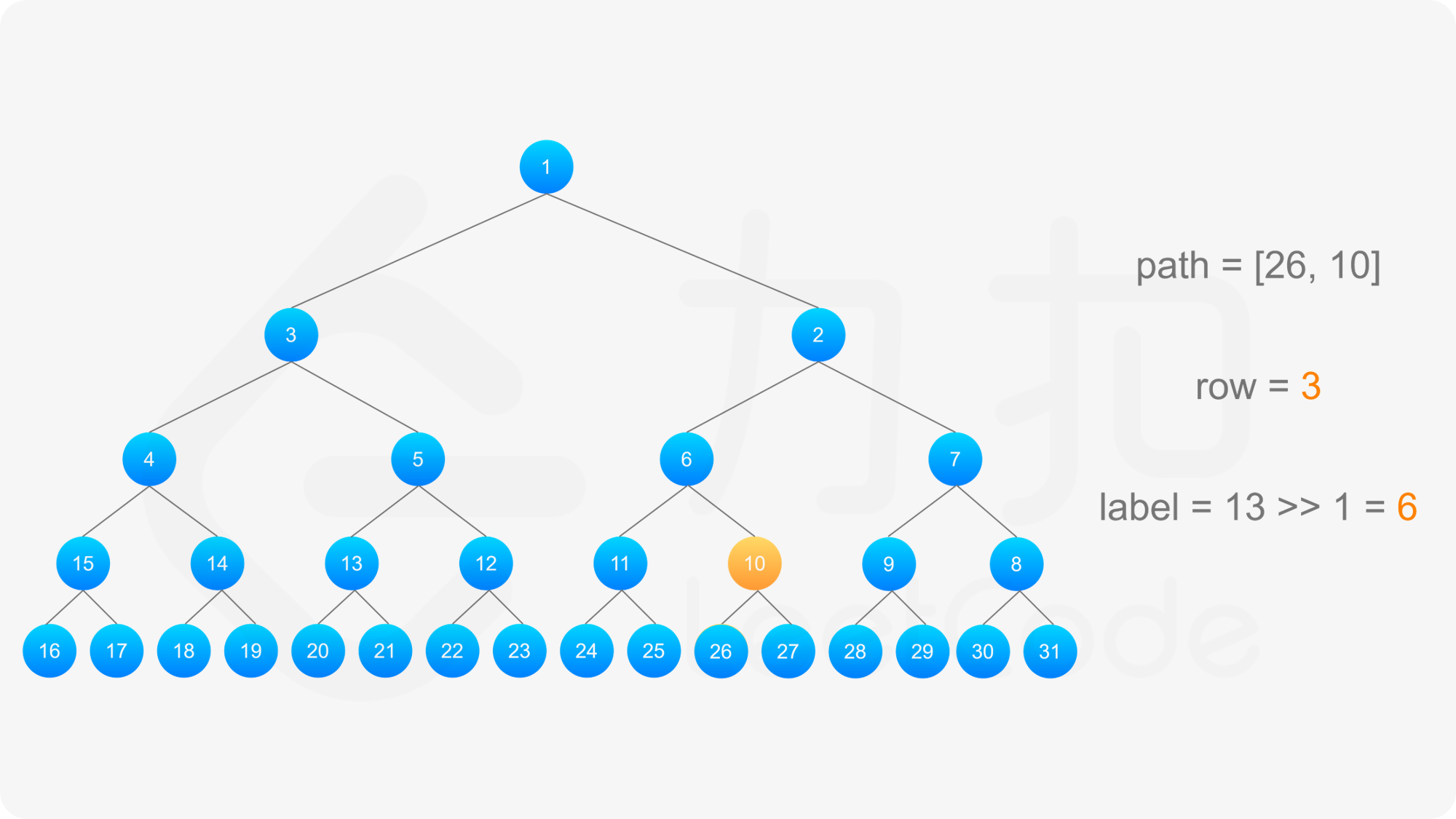
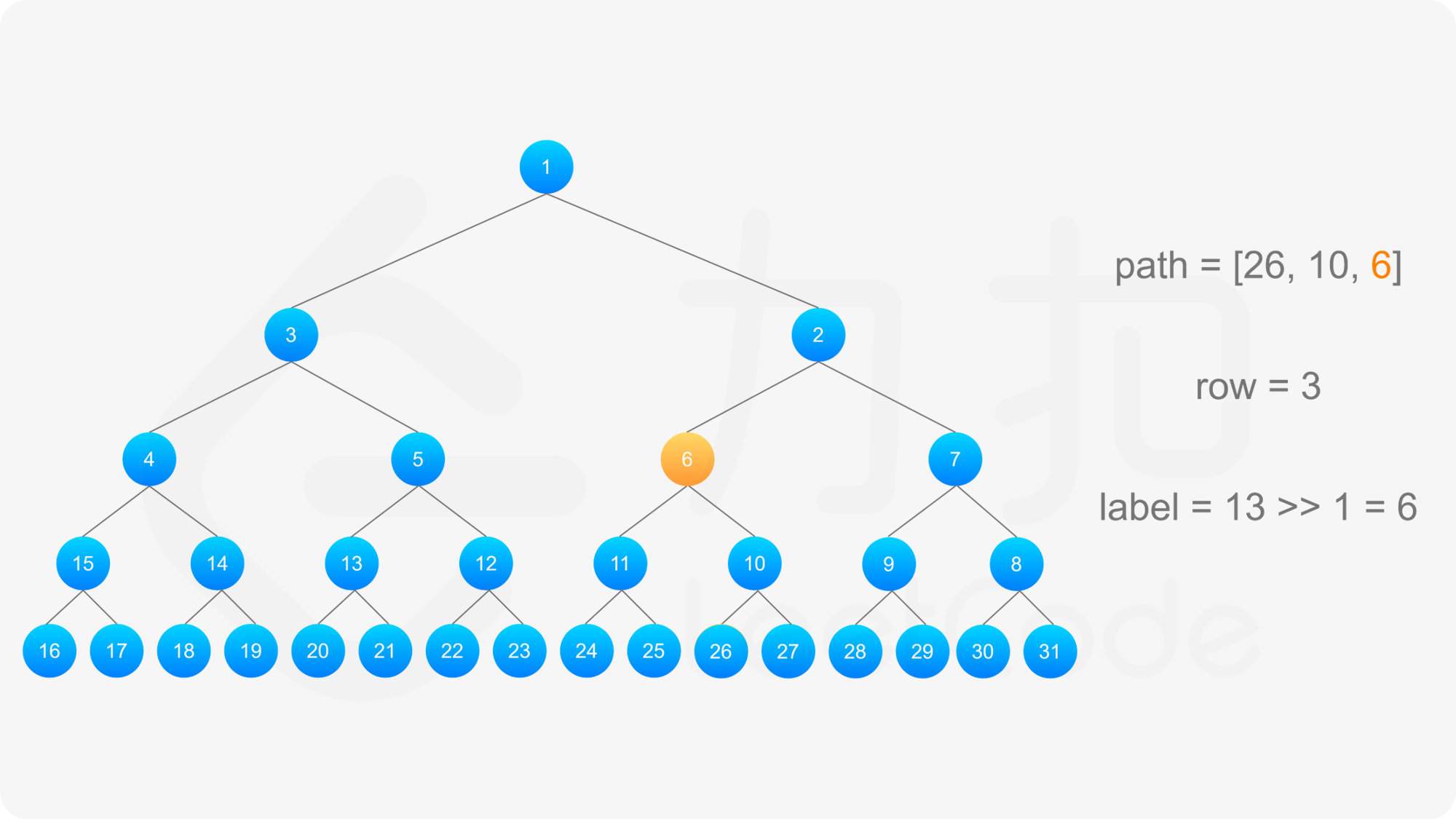
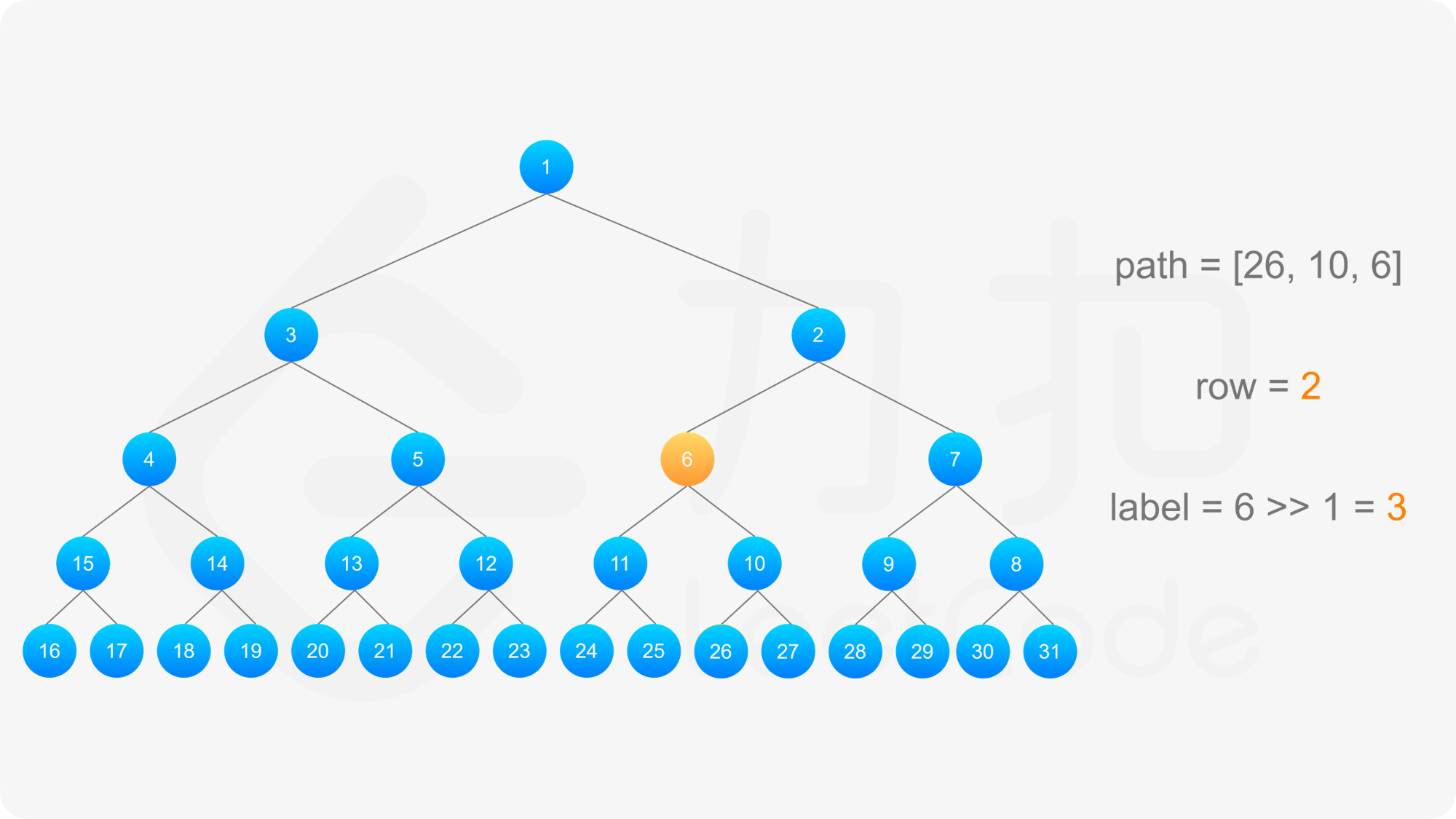
得到标号为 label 的节点的「从左到右标号」之后，即可得到从该节点到根节点的路径，以及路径上的每个节点的「从左到右标号」。对于路径上的每个节点，需要根据节点所在行的奇偶性，得到该节点的实际标号：

  • 当 i 是奇数时，第 i 行的每个节点的「从左到右标号」即为该节点的实际标号；

  • 当 i 是偶数时，如果第 i 行的一个节点的「从左到右标号」为 val，则该节点的实际标号为 2^{i-1} + 2^i - 1 - \textit{val。

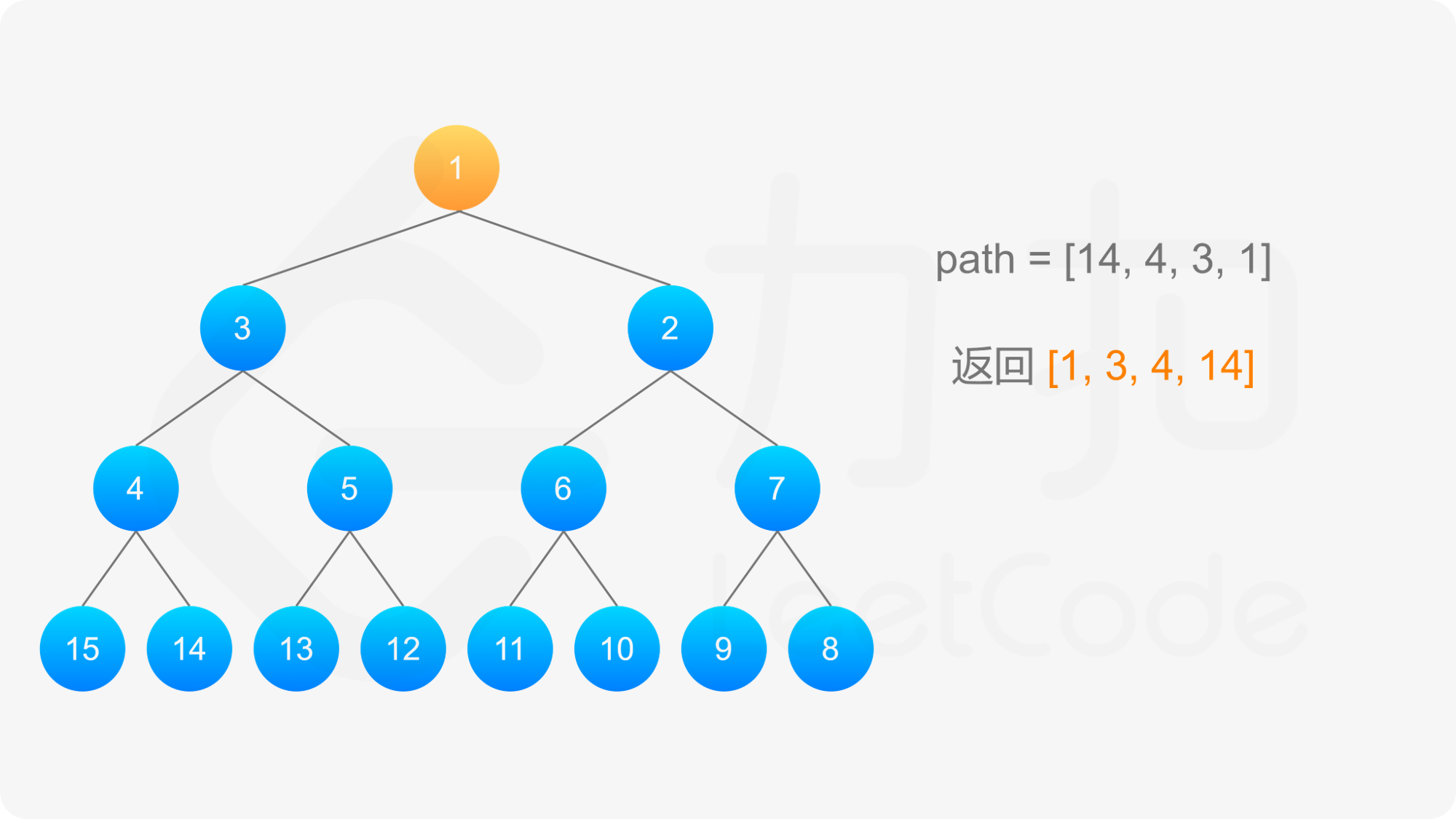
最后，将路径反转，即可得到从根节点到标号 label 的节点的路径。

<fig1,fig2,fig3,fig4,fig5,fig6,fig7,fig8,fig9,fig10,fig11>

<fig12,fig13,fig14,fig15,fig16,fig17,fig18,fig19,fig20,fig21,fig22,fig23>

[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public List<Integer> pathInZigZagTree(int label) {
        int row = 1, rowStart = 1;
        while (rowStart * 2 <= label) {
            row++;
            rowStart *= 2;
        }
        if (row % 2 == 0) {
            label = getReverse(label, row);
        }
        List<Integer> path = new ArrayList<Integer>();
        while (row > 0) {
            if (row % 2 == 0) {
                path.add(getReverse(label, row));
            } else {
                path.add(label);
            }
            row--;
            label >>= 1;
        }
        Collections.reverse(path);
        return path;
    }

    public int getReverse(int label, int row) {
        return (1 << row - 1) + (1 << row) - 1 - label;
    }
}
[sol1-C#]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public class Solution {
    public IList<int> PathInZigZagTree(int label) {
        int row = 1, rowStart = 1;
        while (rowStart * 2 <= label) {
            row++;
            rowStart *= 2;
        }
        if (row % 2 == 0) {
            label = GetReverse(label, row);
        }
        IList<int> path = new List<int>();
        while (row > 0) {
            if (row % 2 == 0) {
                path.Add(GetReverse(label, row));
            } else {
                path.Add(label);
            }
            row--;
            label >>= 1;
        }
        path = new List<int>(path.Reverse());
        return path;
    }

    public int GetReverse(int label, int row) {
        return (1 << row - 1) + (1 << row) - 1 - label;
    }
}
[sol1-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
var pathInZigZagTree = function(label) {
    let row = 1, rowStart = 1;
    while (rowStart * 2 <= label) {
        row++;
        rowStart *= 2;
    }
    if (row % 2 === 0) {
        label = getReverse(label, row);
    }
    const path = [];
    while (row > 0) {
        if (row % 2 === 0) {
            path.push(getReverse(label, row));
        } else {
            path.push(label);
        }
        row--;
        label >>= 1;
    }
    path.reverse();
    return path;
};

const getReverse = (label, row) => {
    return (1 << row - 1) + (1 << row) - 1 - label;
}
[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    int getReverse(int label, int row) {
        return (1 << row - 1) + (1 << row) - 1 - label;
    }

    vector<int> pathInZigZagTree(int label) {
        int row = 1, rowStart = 1;
        while (rowStart * 2 <= label) {
            row++;
            rowStart *= 2;
        }
        if (row % 2 == 0) {
            label = getReverse(label, row);
        }
        vector<int> path;
        while (row > 0) {
            if (row % 2 == 0) {
                path.push_back(getReverse(label, row));
            } else {
                path.push_back(label);
            }
            row--;
            label >>= 1;
        }
        reverse(path.begin(), path.end());
        return path;
    }
};
[sol1-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
void swap(int* a, int* b) {
    int t = *a;
    *a = *b, *b = t;
}

void reverse(int* arr, int left, int right) {
    while (left < right) {
        swap(&arr[left], &arr[right]);
        left++, right--;
    }
}

int getReverse(int label, int row) {
    return (1 << row - 1) + (1 << row) - 1 - label;
}

int* pathInZigZagTree(int label, int* returnSize) {
    int row = 1, rowStart = 1;
    while (rowStart * 2 <= label) {
        row++;
        rowStart *= 2;
    }
    if (row % 2 == 0) {
        label = getReverse(label, row);
    }
    int* path = malloc(sizeof(int) * 20);
    *returnSize = 0;
    while (row > 0) {
        if (row % 2 == 0) {
            path[(*returnSize)++] = getReverse(label, row);
        } else {
            path[(*returnSize)++] = label;
        }
        row--;
        label >>= 1;
    }
    reverse(path, 0, *returnSize - 1);
    return path;
}
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
func getReverse(label, row int) int {
    return 1<<(row-1) + 1<<row - 1 - label
}

func pathInZigZagTree(label int) (path []int) {
    row, rowStart := 1, 1
    for rowStart*2 <= label {
        row++
        rowStart *= 2
    }
    if row%2 == 0 {
        label = getReverse(label, row)
    }
    for row > 0 {
        if row%2 == 0 {
            path = append(path, getReverse(label, row))
        } else {
            path = append(path, label)
        }
        row--
        label >>= 1
    }
    for i, n := 0, len(path); i < n/2; i++ {
        path[i], path[n-1-i] = path[n-1-i], path[i]
    }
    return
}

复杂度分析

  • 时间复杂度：O(\log \textit{label})。标号为 label 的节点所在的行数为 O(\log \textit{label})，因此从根节点到标号 label 的节点的路径的长度为 O(\log \textit{label})，路径中的每个节点的标号都可以在 O(1) 时间内计算得到。

  • 空间复杂度：O(1)。除了返回值以外，额外使用的空间为常数。

 Comments
On this page
1104-二叉树寻路