1110-删点成林

给出二叉树的根节点 root，树上每个节点都有一个不同的值。

如果节点值在 to_delete 中出现，我们就把该节点从树上删去，最后得到一个森林（一些不相交的树构成的集合）。

返回森林中的每棵树。你可以按任意顺序组织答案。

示例 1：

![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2019/07/05/screen-shot-2019-07-01-at-53836-pm.png)

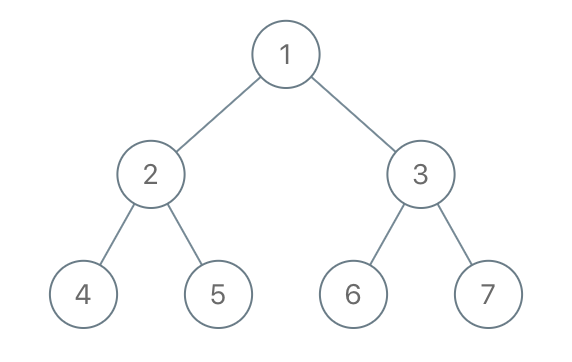
**输入：** root = [1,2,3,4,5,6,7], to_delete = [3,5]
**输出：** [[1,2,null,4],[6],[7]]

示例 2：

**输入：** root = [1,2,4,null,3], to_delete = [3]
**输出：** [[1,2,4]]

提示：

• 树中的节点数最大为 1000。
• 每个节点都有一个介于 1 到 1000 之间的值，且各不相同。
• to_delete.length <= 1000
• to_delete 包含一些从 1 到 1000、各不相同的值。

方法一：深度优先搜索

思路

题目给定一棵树 root，树的每个节点都有一个各不相同的值。并且给定一个数组 to_delete，包含需要删除的节点值。返回删除所有的 to_delete 中的节点后，剩余的树的集合。

可以利用深度优先搜索来遍历每一个节点，定义函数 dfs，输入是参数是某个节点 node 和这个节点是否为潜在的新的根节点 is_root。函数中，首先判断这个节点是否要被删除，如果是，那么它的两个子节点（如果有的话）便成为了潜在的根节点。如果这个节点的值不在 to_delete 中并且 is_root 为 true，那么这个节点便成为了一个新的根节点，需要把它放入结果数组中。同时也要对它的两个子节点进行同样的操作。dfs 的返回值为更新后的 node。

对根节点调用一次 dfs，返回新的根节点数组即可。

代码

[sol1-Python3]

class Solution:
    def delNodes(self, root: Optional[TreeNode], to_delete: List[int]) -> List[TreeNode]:
        to_delete_set = set(to_delete)
        roots = []
        self.dfs(root, True, to_delete_set, roots)
        return roots

    def dfs(self, node: Optional[TreeNode], is_root: bool, to_delete_set: set[int], roots: List[TreeNode]) ->  Optional[TreeNode]:
        if node == None:
            return None
        delete = node.val in to_delete_set
        node.left = self.dfs(node.left, delete, to_delete_set, roots)
        node.right = self.dfs(node.right, delete, to_delete_set, roots)
        if delete:
            return None
        else:
            if is_root:
                roots.append(node)
            return node

[sol1-Java]

class Solution {
    public List<TreeNode> delNodes(TreeNode root, int[] to_delete) {
        Set<Integer> toDeleteSet = new HashSet<Integer>();
        for (int val : to_delete) {
            toDeleteSet.add(val);
        }
        List<TreeNode> roots = new ArrayList<TreeNode>();
        dfs(root, true, toDeleteSet, roots);
        return roots;
    }

    public TreeNode dfs(TreeNode node, boolean isRoot, Set<Integer> toDeleteSet, List<TreeNode> roots) {
        if (node == null) {
            return null;
        }
        boolean deleted = toDeleteSet.contains(node.val);
        node.left = dfs(node.left, deleted, toDeleteSet, roots);
        node.right = dfs(node.right, deleted, toDeleteSet, roots);
        if (deleted) {
            return null;
        } else {
            if (isRoot) {
                roots.add(node);
            }
            return node;
        }
    }
}

[sol1-Go]

func delNodes(root *TreeNode, to_delete []int) []*TreeNode {
    toDeleteSet := make(map[int]bool)
    for _, val := range to_delete {
        toDeleteSet[val] = true
    }
    var roots []*TreeNode
    dfs(root, true, toDeleteSet, &roots)
    return roots
}

func dfs(node *TreeNode, isRoot bool, toDeleteSet map[int]bool, roots *[]*TreeNode) *TreeNode {
    if node == nil {
        return nil
    }
    deleted := toDeleteSet[node.Val]
    node.Left = dfs(node.Left, deleted, toDeleteSet, roots)
    node.Right = dfs(node.Right, deleted, toDeleteSet, roots)
    if deleted {
        return nil
    } else {
        if isRoot {
            *roots = append(*roots, node)
        }
        return node
    }
}

[sol1-JavaScript]

var delNodes = function(root, to_delete) {
    const toDeleteSet = new Set(to_delete);
    const roots = [];
    dfs(root, true, toDeleteSet, roots);
    return roots;
}

function dfs(node, isRoot, toDeleteSet, roots) {
    if (!node) {
        return null;
    }
    const deleted = toDeleteSet.has(node.val);
    node.left = dfs(node.left, deleted, toDeleteSet, roots);
    node.right = dfs(node.right, deleted, toDeleteSet, roots);
    if (deleted) {
        return null;
    } else {
        if (isRoot) {
            roots.push(node);
        }
        return node;
    }
}

[sol1-C#]

public class Solution {
    public IList<TreeNode> DelNodes(TreeNode root, int[] to_delete) {
        ISet<int> toDeleteSet = new HashSet<int>();
        foreach (int val in to_delete) {
            toDeleteSet.Add(val);
        }
        IList<TreeNode> roots = new List<TreeNode>();
        DFS(root, true, toDeleteSet, roots);
        return roots;
    }

    public TreeNode DFS(TreeNode node, bool isRoot, ISet<int> toDeleteSet, IList<TreeNode> roots) {
        if (node == null) {
            return null;
        }
        bool deleted = toDeleteSet.Contains(node.val);
        node.left = DFS(node.left, deleted, toDeleteSet, roots);
        node.right = DFS(node.right, deleted, toDeleteSet, roots);
        if (deleted) {
            return null;
        } else {
            if (isRoot) {
                roots.Add(node);
            }
            return node;
        }
    }
}

[sol1-C++]

class Solution {
public:
    vector<TreeNode*> delNodes(TreeNode* root, vector<int>& to_delete) {
        unordered_set<int> to_delete_set(to_delete.begin(), to_delete.end());
        vector<TreeNode *> roots;

        function<TreeNode *(TreeNode *, bool)> dfs = [&](TreeNode* node, bool is_root) -> TreeNode * {
            if (node == nullptr) {
                return nullptr;
            }
            bool deleted = to_delete_set.count(node->val) ? true : false;
            node->left = dfs(node->left, deleted);
            node->right = dfs(node->right, deleted);
            if (deleted) {
                return nullptr;
            } else {
                if (is_root) {
                    roots.emplace_back(node);
                }
                return node;
            }
        };

        dfs(root, true);
        return roots;
    }
};

[sol1-C]

#define MAX_NODES 1000

typedef struct {
    int key;
    UT_hash_handle hh;
} HashItem; 

HashItem *hashFindItem(HashItem **obj, int key) {
    HashItem *pEntry = NULL;
    HASH_FIND_INT(*obj, &key, pEntry);
    return pEntry;
}

bool hashAddItem(HashItem **obj, int key) {
    if (hashFindItem(obj, key)) {
        return false;
    }
    HashItem *pEntry = (HashItem *)malloc(sizeof(HashItem));
    pEntry->key = key;
    HASH_ADD_INT(*obj, key, pEntry);
    return true;
}

void hashFree(HashItem **obj) {
    HashItem *curr = NULL, *tmp = NULL;
    HASH_ITER(hh, *obj, curr, tmp) {
        HASH_DEL(*obj, curr);  
        free(curr);
    }
}

struct TreeNode* dfs(struct TreeNode* node, bool is_root, const HashItem *to_delete_set, struct TreeNode** roots, int *pos) {
    if (node == NULL) {
        return NULL;
    }
    bool deleted = hashFindItem(&to_delete_set, node->val) != NULL ? true : false;
    node->left = dfs(node->left, deleted, to_delete_set, roots, pos);
    node->right = dfs(node->right, deleted, to_delete_set, roots, pos);
    if (deleted) {
        return NULL;
    } else {
        if (is_root) {
            roots[(*pos)++] = node;
        }
        return node;
    }
};

struct TreeNode** delNodes(struct TreeNode* root, int* to_delete, int to_deleteSize, int* returnSize) {
    struct TreeNode** roots = (struct TreeNode**)malloc(sizeof(struct TreeNode *) * MAX_NODES);
    int pos = 0;
    HashItem *to_delete_set = NULL;
    for (int i = 0; i < to_deleteSize; i++) {
        hashAddItem(&to_delete_set, to_delete[i]);
    }
    dfs(root, true, to_delete_set, roots, &pos);
    *returnSize = pos;
    hashFree(&to_delete_set);
    return roots;
}

复杂度分析

• 时间复杂度：O(n)，其中 n 是树的节点数。

• 空间复杂度：O(n)，其中 n 是树的节点数。