环形公交路线上有 n 个站,按次序从 0 到 n - 1 进行编号。我们已知每一对相邻公交站之间的距离,distance[i] 表示编号为
i 的车站和编号为 (i + 1) % n 的车站之间的距离。
环线上的公交车都可以按顺时针和逆时针的方向行驶。
返回乘客从出发点 start 到目的地 destination 之间的最短距离。
示例 1:
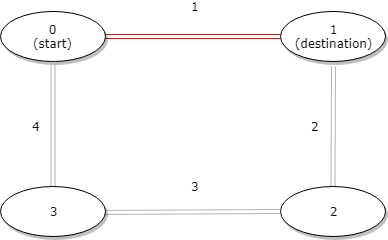
**输入:** distance = [1,2,3,4], start = 0, destination = 1
**输出:** 1
**解释:** 公交站 0 和 1 之间的距离是 1 或 9,最小值是 1。
示例 2:
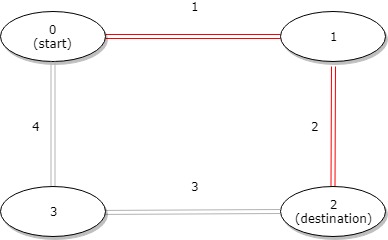
**输入:** distance = [1,2,3,4], start = 0, destination = 2
**输出:** 3
**解释:** 公交站 0 和 2 之间的距离是 3 或 7,最小值是 3。
示例 3:
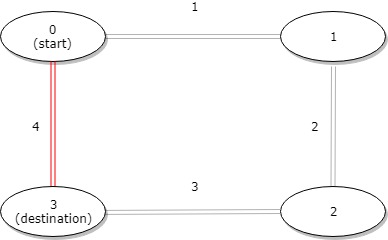
**输入:** distance = [1,2,3,4], start = 0, destination = 3
**输出:** 4
**解释:** 公交站 0 和 3 之间的距离是 6 或 4,最小值是 4。
提示:
1 <= n <= 10^4distance.length == n0 <= start, destination < n0 <= distance[i] <= 10^4
方法一:一次遍历
记数组 distance 的长度为 n。假设 start} \le \textit{destination,那么我们可以:
- 从 start 到 destination,距离为 \sum\limits_{i=\textit{start} }^{\textit{destination}-1}\textit{distance}[i];
- 从 start 到 0,再从 0 到 destination,距离为 \sum\limits_{i=0}^{\textit{start}-1}\textit{distance}[i]+\sum\limits_{i=\textit{destination} }^{n-1}\textit{distance}[i]。
答案为这两个距离的最小值。
[sol1-Python3]1
2
3
4
5
| class Solution:
def distanceBetweenBusStops(self, distance: List[int], start: int, destination: int) -> int:
if start > destination:
start, destination = destination, start
return min(sum(distance[start:destination]), sum(distance[:start]) + sum(distance[destination:]))
|
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
| class Solution {
public:
int distanceBetweenBusStops(vector<int>& distance, int start, int destination) {
if (start > destination) {
swap(start, destination);
}
return min(accumulate(distance.begin() + start, distance.begin() + destination, 0),
accumulate(distance.begin(), distance.begin() + start, 0) +
accumulate(distance.begin() + destination, distance.end(), 0));
}
};
|
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
public int distanceBetweenBusStops(int[] distance, int start, int destination) {
if (start > destination) {
int temp = start;
start = destination;
destination = temp;
}
int sum1 = 0, sum2 = 0;
for (int i = 0; i < distance.length; i++) {
if (i >= start && i < destination) {
sum1 += distance[i];
} else {
sum2 += distance[i];
}
}
return Math.min(sum1, sum2);
}
}
|
[sol1-C#]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| public class Solution {
public int DistanceBetweenBusStops(int[] distance, int start, int destination) {
if (start > destination) {
int temp = start;
start = destination;
destination = temp;
}
int sum1 = 0, sum2 = 0;
for (int i = 0; i < distance.Length; i++) {
if (i >= start && i < destination) {
sum1 += distance[i];
} else {
sum2 += distance[i];
}
}
return Math.Min(sum1, sum2);
}
}
|
[sol1-Golang]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| func distanceBetweenBusStops(distance []int, start, destination int) int {
if start > destination {
start, destination = destination, start
}
sum1, sum2 := 0, 0
for i, d := range distance {
if start <= i && i < destination {
sum1 += d
} else {
sum2 += d
}
}
return min(sum1, sum2)
}
func min(a, b int) int {
if a > b {
return b
}
return a
}
|
[sol1-C]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| #define MIN(a, b) ((a) < (b) ? (a) : (b))
int distanceBetweenBusStops(int* distance, int distanceSize, int start, int destination){
if (start > destination) {
int temp = start;
start = destination;
destination = temp;
}
int sum1 = 0, sum2 = 0;
for (int i = 0; i < distanceSize; i++) {
if (i >= start && i < destination) {
sum1 += distance[i];
} else {
sum2 += distance[i];
}
}
return MIN(sum1, sum2);
}
|
[sol1-JavaScript]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| var distanceBetweenBusStops = function(distance, start, destination) {
if (start > destination) {
const temp = start;
start = destination;
destination = temp;
}
let sum1 = 0, sum2 = 0;
for (let i = 0; i < distance.length; i++) {
if (i >= start && i < destination) {
sum1 += distance[i];
} else {
sum2 += distance[i];
}
}
return Math.min(sum1, sum2);
};
|
复杂度分析