1202-交换字符串中的元素
给你一个字符串 s,以及该字符串中的一些「索引对」数组 pairs,其中 pairs[i] = [a, b] 表示字符串中的两个索引(编号从 0
开始)。
你可以 任意多次交换 在 pairs 中任意一对索引处的字符。
返回在经过若干次交换后,s 可以变成的按字典序最小的字符串。
示例 1:
**输入:** s = "dcab", pairs = [[0,3],[1,2]]
**输出:** "bacd"
**解释:**
交换 s[0] 和 s[3], s = "bcad"
交换 s[1] 和 s[2], s = "bacd"
示例 2:
**输入:** s = "dcab", pairs = [[0,3],[1,2],[0,2]]
**输出:** "abcd"
**解释:**
交换 s[0] 和 s[3], s = "bcad"
交换 s[0] 和 s[2], s = "acbd"
交换 s[1] 和 s[2], s = "abcd"
示例 3:
**输入:** s = "cba", pairs = [[0,1],[1,2]]
**输出:** "abc"
**解释:**
交换 s[0] 和 s[1], s = "bca"
交换 s[1] 和 s[2], s = "bac"
交换 s[0] 和 s[1], s = "abc"
提示:
1 <= s.length <= 10^50 <= pairs.length <= 10^50 <= pairs[i][0], pairs[i][1] < s.lengths中只含有小写英文字母
📺 视频讲解
力扣君温馨小贴士:觉得视频时间长的扣友,可以在视频右下角的「设置」按钮处选择 1.5 倍速或者 2 倍速观看。
📖 文字解析
关于字典序的定义,大家可以查阅 字典序 - 百度百科 。根据定义,ASCII 值越小的字符位于字符串中的位置越靠前,整个字符串的字典序就越靠前。
改变字符串中字符位置的操作是输入数组 pairs 中的「索引对」,每一个「索引对」表示一次「交换索引对应的字符」操作。我们需要想办法让 ASCII 值小的字符交换到字符串中靠前的位置。
分析示例
示例 1:输入:s = "dcab", pairs = [[0, 3], [1, 2]]:
- 交换
s[0]和s[3],让 ASCII 值小的字符b靠前; - 交换
s[1]和s[2],让 ASCII 值小的字符a靠前;
这样得到的字符串 "bacd" 字典序最小。
示例 2:输入 s = "dcab", pairs = [[0, 3], [1, 2], [0, 2]]
示例 2 与示例 1 的输入是一样的,pairs 多了一对索引对 [0, 2],由于多了这个索引对,s 的 4 个索引可以任意交换,这是因为 交换关系具有传递性。
理解「交换关系具有传递性」:
[0, 3]和[0, 2]有共同索引0,说明索引0、2、3可以任意交换;[1, 2]和[0, 2]有共同索引2,说明索引0、1、2可以任意交换; 因此[0, 2]把[0, 3]和[1, 2]中出现的索引0、1、2、3连在了一起。
题目中说「可以 任意多次交换 在 pairs 中任意一对索引处的字符」。于是我们可以将 0、1、2、3 这 4 个索引位置上的字符按照 ASCII 值升序排序。采用基于比较的原地排序算法(选择排序、插入排序、冒泡排序、快速排序)均可。
(示例 3 与示例 2 的分析一样,这里省略。)
通过对示例的分析,我们知道,当前问题是一个图论的问题,我们需要找出同属于一个连通分量的所有字符。把「连在一起」的索引按照字符的 ASCII 值升序排序。交换关系具有传递性、找哪些索引连在一起、数组 pairs 给出的是数对的形式,这三点提示我们可以使用并查集。
方法:并查集
根据上面的分析,我们设计算法步骤如下:
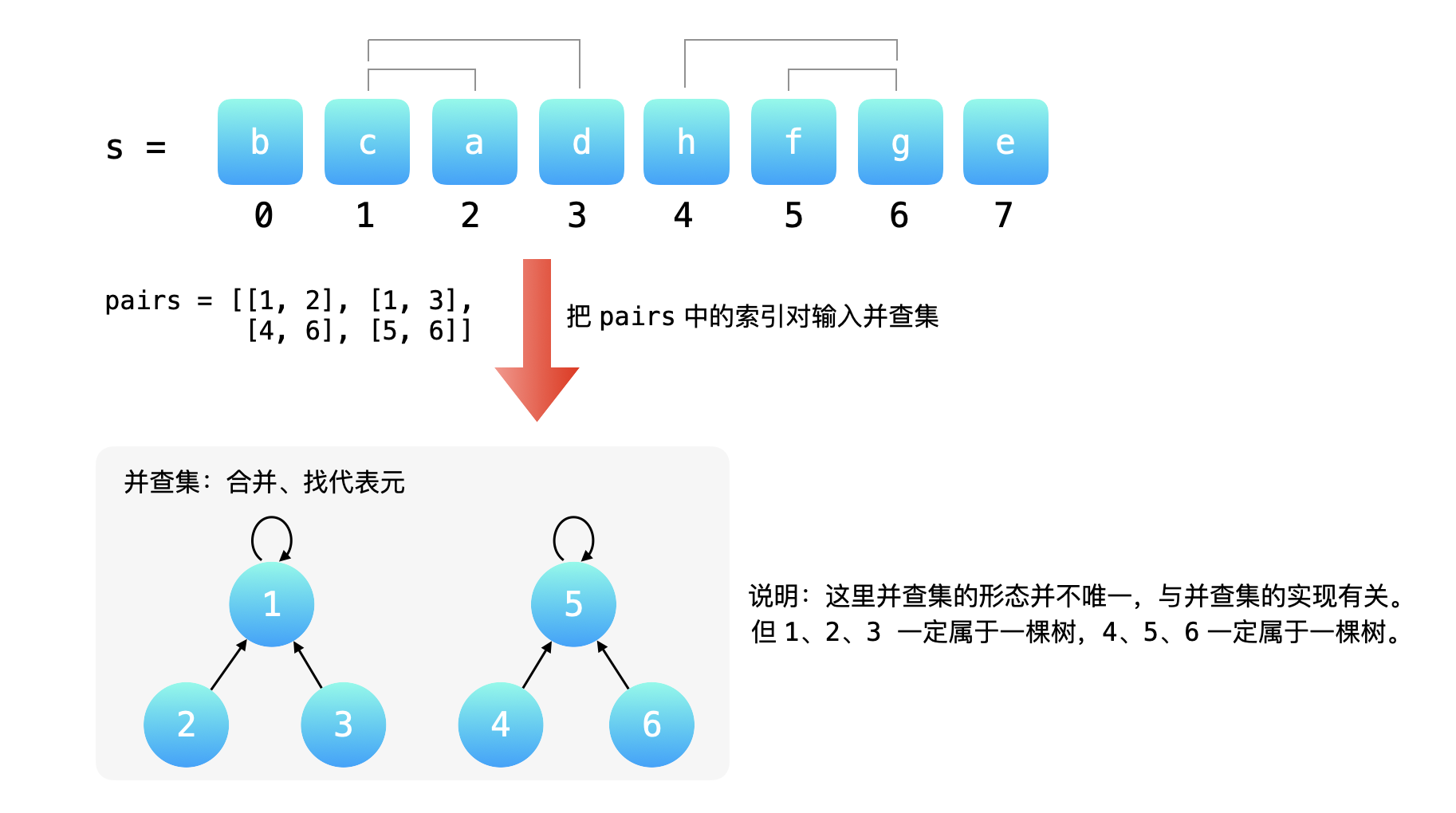
第 1 步:先遍历 pairs 中的索引对,将索引对中成对的索引输入并查集,并查集会帮助我们实现同属于一个连通分量中的元素的合并工作。注意:并查集管理的是「索引」不是「字符」。
 {:width=500}
{:width=500}
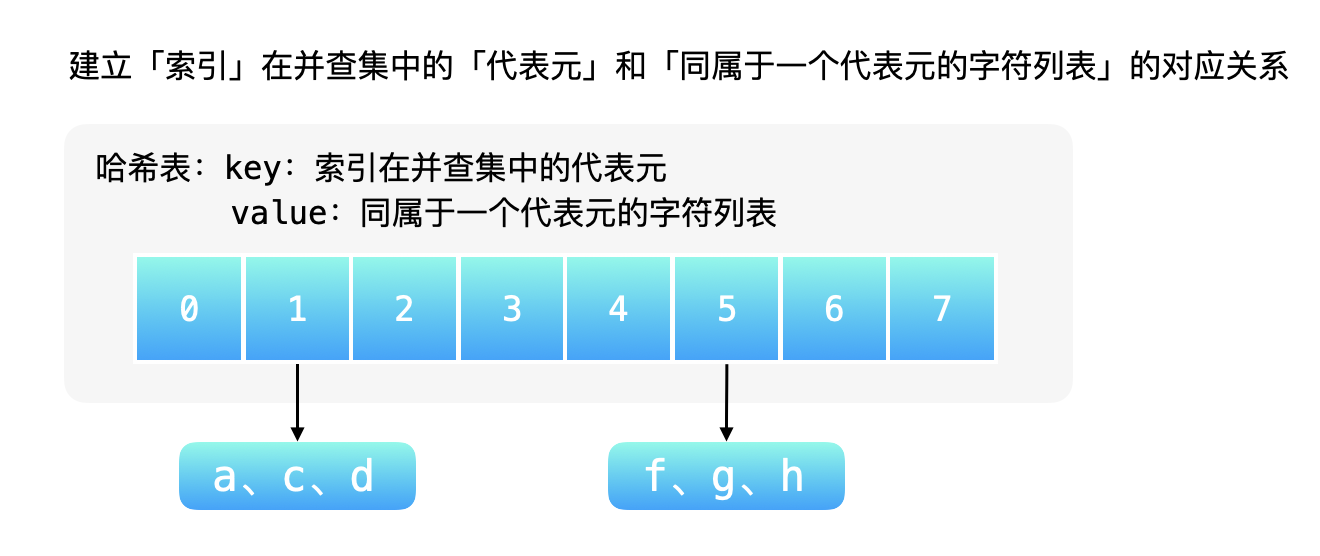
第 2 步:遍历输入字符串 s,对于每一个索引,找到这个索引在并查集中的代表元,把同属于一个代表元的字符放在一起。这一步需要建立一个映射关系。键:并查集中的代表元,值:同属于一个代表元的 s 中的字符。可以使用哈希表建立映射关系。
 {:width=500}
{:width=500}
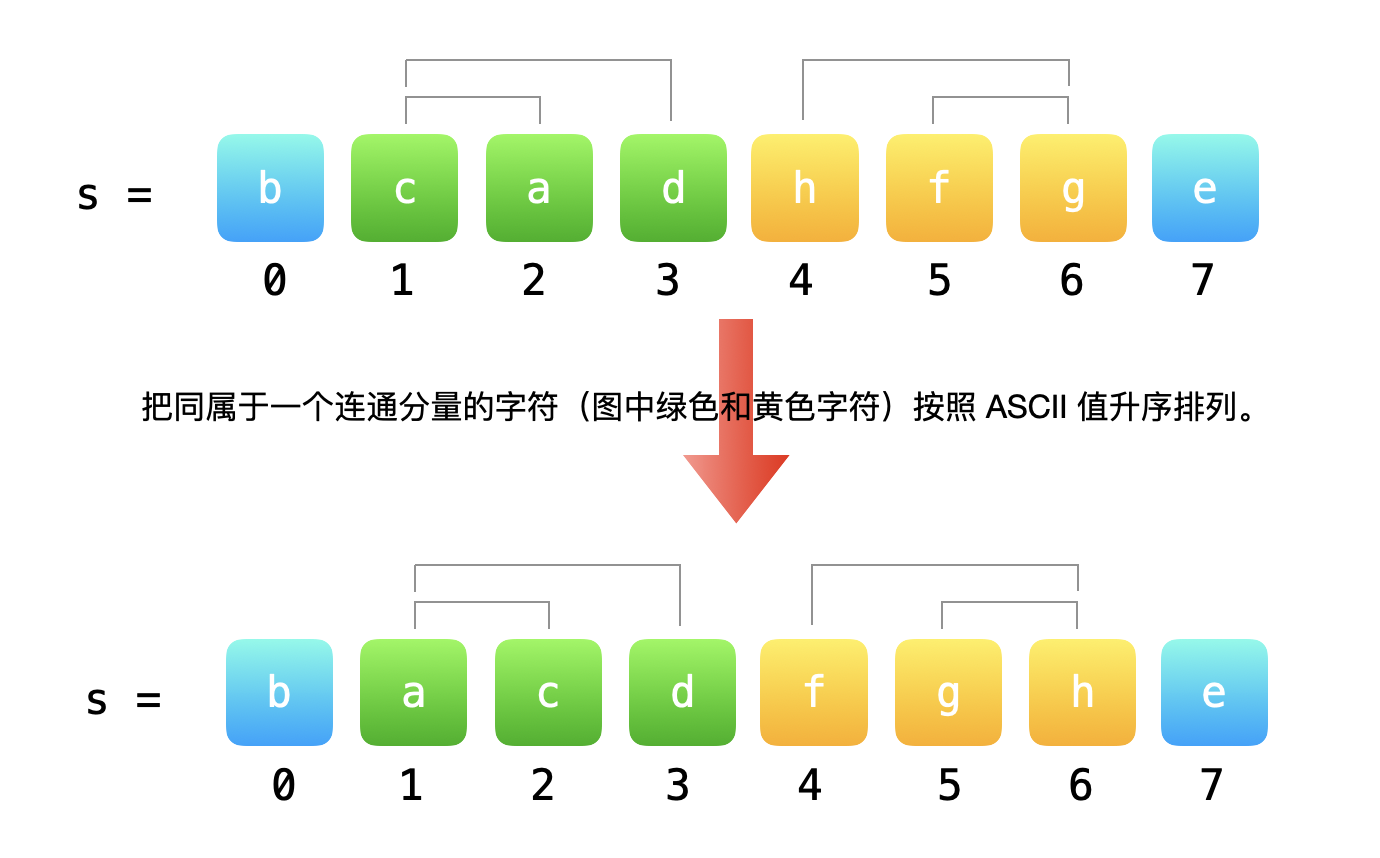
第 3 步:分组排序。即对同属于一个连通分量中的字符进行排序。
 {:width=500}
{:width=500}
这一步实现可以这样做:重新生成一个长度和 s 相同的字符串,对于每一个索引,查询索引在并查集中的代表元,再从哈希表中获得这个代表元对应的字符集列表,从中移除 ASCII 值最小的字符依次拼接起来。
这一步我们每一次需要从一个集合中选出 ASCII 值最小的字符,选出以后不再用它,带排序功能的集合有「平衡树(二叉搜索树)」和「优先队列(堆)」等,可以使用「优先队列」。
参考代码:
1 | import java.util.HashMap; |
说明:
- 这一版并查集引入了「按秩合并」,「按秩合并」在这个问题里不是必需的。「按秩合并」又叫「启发式合并」,「启发」的意思是:「依据经验」、「尝试」、「探测」,在可接受误差的情况下行之有效的算法策略。简而言之:虽然不精确、达不到最优,但好过没有;
- 「路径压缩」和「按秩合并」一起使用的时候,难以维护「秩」准确的定义,但依然具有参考价值。这是因为:虽然
rank不是此时树的精确高度,但是不会出现树a的高度比树b结点高,但是树a的rank却比树b的rank低的情况。
复杂度分析:
时间复杂度:O((M + N) \alpha (N) + N \log N),这里 M是数组
pairs的长度,N 是输入字符串s的长度,这里 \alpha 是 Ackermann 函数的反函数(请见参考资料);- 第 1 步:遍历数组
pairs需要 O(M),,并查集每一次合并(按秩合并)的同时还有路径压缩,时间复杂度为 O(\alpha(N)),这一部分总的时间复杂度为 O(M \alpha(N)); - 第 2 步:并查集每一次查询的时间复杂度为 O(\alpha(N)),一共 N 次查询,时间复杂度为 O(N \alpha(N)),每一个字符加入优先队列。极端情况下,所有字符都在一个优先队列里,每一次调整堆的时间复杂度为 O(\log N),这一部分总的时间复杂度为 O\left(N (\alpha(N) + \log N)\right);
- 第 3 步:极端情况下,所有的字符都在一个连通分量里(所有字符都在一个优先队列里),并查集每一次查询的时间复杂度为 O(\alpha(N)),在优先队列里选出字典序最小的字符时间复杂度为 O(\log N),一共 N 次调整堆,这一部分总的时间复杂度也为 O\left(N (\alpha(N) + \log N)\right)。
- 第 1 步:遍历数组
空间复杂度:O(N):并查集的长度为 N ,哈希表的长度为 N,所有的优先队列中加起来一共有 N 个字符,保存结果需要 N 个字符。
同时使用「路径压缩」和「按秩合并」的时间复杂度
同时使用了「按秩合并」和「路径压缩」的「并查集」,单次「合并」与「查询」操作的时间复杂度为 Ackermann 函数 的反函数,记为 \alpha。此时并查集的时间复杂度使用 \alpha 表示。大家可以在「参考资料」里阅读关于该函数的介绍。需要知道的结论如下:
\alpha(N) 的增长极其缓慢,对于实际应用中可能出现的所有 N 值均小于 5 (来自《算法(第 4 版)》提高题 1.5.13)。
下面是一个经验,并不绝对,仅供大家参考:在实际解决问题的时候,一般只用「路径压缩」。如果「路径压缩」的结果不太理想,再考虑使用「按秩合并」。虽然「路径压缩」和「按秩合并」同时使用在理论上会使得时间复杂度降低,但在数据规模有限的情况下,这种优化可能不能加快程序的执行时间。具体情况需要具体分析。
参考资料
- 《算法导论(第 3 版)》第 21 章:用于不相交集合的数据结构;
- 《算法》(第 4 版)第 1 章第 5 节:案例研究:union-find 算法;
- OI Wiki - 数据结构 - 并查集 。
