1203-项目管理
有 n 个项目,每个项目或者不属于任何小组,或者属于 m 个小组之一。group[i] 表示第 i 个项目所属的小组,如果第 i
个项目不属于任何小组,则 group[i] 等于 -1。项目和小组都是从零开始编号的。可能存在小组不负责任何项目,即没有任何项目属于这个小组。
请你帮忙按要求安排这些项目的进度,并返回排序后的项目列表:
- 同一小组的项目,排序后在列表中彼此相邻。
- 项目之间存在一定的依赖关系,我们用一个列表
beforeItems来表示,其中beforeItems[i]表示在进行第i个项目前(位于第i个项目左侧)应该完成的所有项目。
如果存在多个解决方案,只需要返回其中任意一个即可。如果没有合适的解决方案,就请返回一个 空列表 。
示例 1:
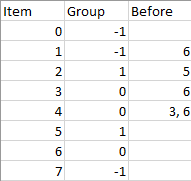
**输入:** n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3,6],[],[],[]]
**输出:** [6,3,4,1,5,2,0,7]
示例 2:
**输入:** n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3],[],[4],[]]
**输出:** []
**解释:** 与示例 1 大致相同,但是在排序后的列表中,4 必须放在 6 的前面。
提示:
1 <= m <= n <= 3 * 104group.length == beforeItems.length == n-1 <= group[i] <= m - 10 <= beforeItems[i].length <= n - 10 <= beforeItems[i][j] <= n - 1i != beforeItems[i][j]beforeItems[i]不含重复元素
📺 视频讲解
视频时间线:
- 解读题意:00:10
- 拓扑排序简介:03:36
- 示例 1 分析:07:50
- 编码前的思路分析:09:59
- 参考代码:12:18
- 复杂度分析、练习:21:22
力扣君温馨小贴士:
- 觉得视频时间长的扣友,可以在视频右下角的「设置」按钮处选择 1.5 倍速或者 2 倍速观看;
- 如果已经充分了解了题意,对「拓扑排序」这个知识点已经非常熟悉的朋友,可以直接观看「编码前的思路分析」(09:59 开始)。
📖 文字解析
这个问题标注为「困难」,但是解决这个问题用到的知识点其实大家都见过。要点和提示如下:
- 从问题的描述(任务计划安排)和结果要求(有可能不存在,如果有,可能不唯一),可以看出思路是「拓扑排序」;
- 读懂题目的意思,这一点非常重要,弄清楚输入的每一个变量的含义,弄清楚什么叫「无人接手」以及
group[i] = - 1的含义; - 安排任务的第一优先级:组(
group)相同的项目必须排在一起,第二优先级:项目(item)的先后顺序满足拓扑序; - 关键 1:题目给出的
item和beforItem可以得到item须要满足的先后顺序。而每一个item或者对应一个group,或者不属于任何一个给定的group,根据item和group的函数关系(从item可以得到唯一的group编号):可以得到安排组(group)的先后顺序(这一点很关键); - 关键 2:分别对
group和item执行拓扑排序,从item -> group的(多对一关系)反向得到group -> item的一对多关系,由于item按照拓扑序排列,建立group到item的一对多关系以后,每一个group对应的item列表是符合拓扑序的; - 从
group的拓扑序,和group到item的一对多关系,得到的item列表就是满足题目意思的一个结果。
下面是详解。
方法:拓扑排序
1. 如何得到组 group 的先后关系
- 如果不考虑「同一小组的项目,排序后在列表中彼此相邻」。根据
beforeItems可以得到项目item的拓扑排序结果; - 由数组
group可以得到项目item对应的组的编号。
由以上两点,可以得到 组 group 的先后关系。
以示例 1 为例:

表格第 2 行(不计算表头):项目 6 (组号 0)必需在项目 1 (不属于任何组,暂时记组号为 2)的前面,可以得出:组号为 0 的所有项目应该位于组号为 2 的所有项目的前面。
有可能出现这种情况:前驱项目和当前项目分在一组,这样的数据需要舍弃,例如第 5 行。项目 3 、项目 6 必需被安排在项目 4 的前面,但是它们的组号都为 0。
2. 如何让相同组号的项目在一起
由上一步的结果得到「组的先后关系」,进而得到组 group 的拓扑排序结果。而 同组的项目也必须满足先后顺序,因此必需对项目 item 也执行一次拓扑排序。
按照项目 item 的拓扑排序结果,依次 把它们映射到对应的组 group 里,这一步需要建立一个映射关系:key 是组编号,value 是同一组的项目按照拓扑排序的结果。
再根据组 group 的拓扑排序的结果,以及上一步建立的映射关系,把 group 映射到 item 列表,就得到了题目要求的 ① 同组项目放在一起 ② 且项目之间还满足拓扑序的拓扑排序结果。
3. 细节:为什么须要给 group[i] = -1 的项目赋值为一个新的组号?
根据题意,group[i] = -1 表示编号为 i 的项目,不属于编号为 0 到 m - 1 的这 m 个组,换句话说,完成这些项目不需要协同合作。
又因为我们需要根据「组」的先后顺序得到「组的拓扑排序的结果」。为了避免我们设计的算法认为 group[i] = -1 的这些项目都在同一组,因此给 group[i] = -1 的这些组一个不同于 0 到 m - 1 的编号,从 m 开始逐个给每个项目编号即可。
参考代码:
1 | import java.util.ArrayList; |
复杂度分析:
说明:这里为了表达严谨,时间复杂度和空间复杂度的描述比较理论化。大家未必须要深究。就当前这个问题而言,拓扑排序就是就是在图中进行一次广度优先遍历,时间复杂度为图的顶点数加边数,假设当前问题的图结构的顶点数为 V、边数为 E,可以简记时间复杂度为 O(V + E)。
时间复杂度:O(m + n^2 + E_{group} + E_{item} ),这里 n 是项目的总数,m 是组的总数(把标记为 -1 的组预处理以后,新的组的总数不会超过 2m);
- 对组的数据进行预处理 O(m);
- 构建组的邻接表 O(m)、项目的邻接表 O(n^2),遍历
before,最极端情况下,第 1 个顶点指向所有剩余 n - 1 个顶点,第 2 个顶点指向所有剩余 n - 2 个顶点,……; - 构建组的入度数组 O(m)、项目入度数组 O(n);
- 执行组的拓扑排序O(m + E_{group})、项目的拓扑排序 O(n + E_{item})。这里用 E_{group 表示组的邻接表的边数, E_{item 表示项目的邻接表的边数;
- 构建组到项目的一对多关系 O(m + n);
- 输出符合题目要求的结果 O(m + n)。
空间复杂度:O(m + n^2);
- 组的邻接表 O(m)、项目的邻接表 O(n^2);
- 组的入度数组 O(m)、项目入度数组 O(n);
- 组到项目的一对多关系 O(m + n);
- 符合题目要求的结果 O(m + n)。
