1217-玩筹码
有 n 个筹码。第 i 个筹码的位置是 position[i] 。
我们需要把所有筹码移到同一个位置。在一步中,我们可以将第 i 个筹码的位置从 position[i] 改变为:
position[i] + 2或position[i] - 2,此时cost = 0position[i] + 1或position[i] - 1,此时cost = 1
返回将所有筹码移动到同一位置上所需要的 最小代价 。
示例 1:
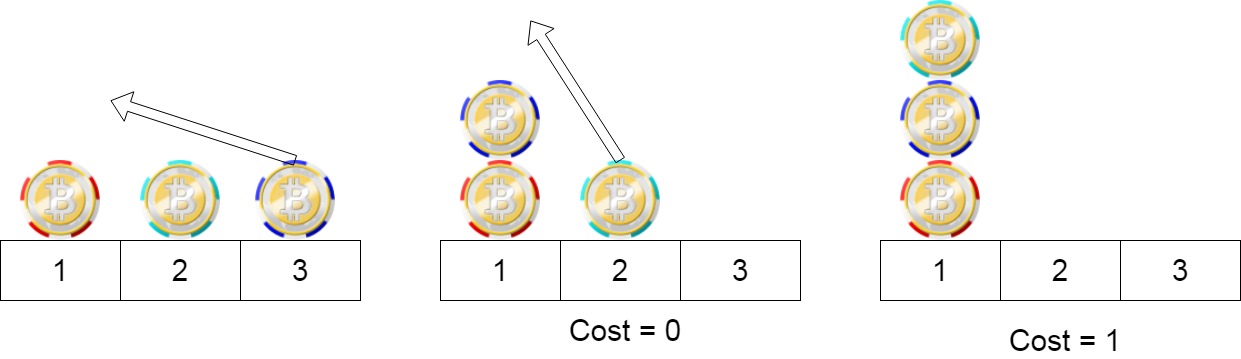
**输入:** position = [1,2,3]
**输出:** 1
**解释:** 第一步:将位置3的筹码移动到位置1,成本为0。
第二步:将位置2的筹码移动到位置1,成本= 1。
总成本是1。
示例 2:
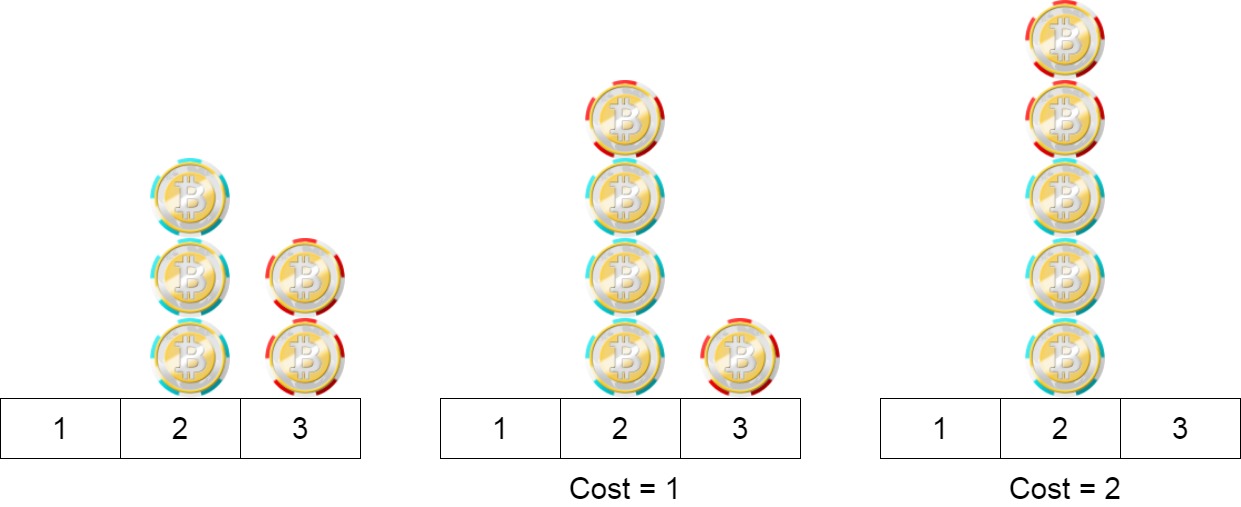
**输入:** position = [2,2,2,3,3]
**输出:** 2
**解释:** 我们可以把位置3的两个筹码移到位置2。每一步的成本为1。总成本= 2。
示例 3:
**输入:** position = [1,1000000000]
**输出:** 1
提示:
1 <= position.length <= 1001 <= position[i] <= 10^9
方法一:贪心
思路与算法
首先很容易得出:
- 从某一个偶(奇)数位置 p_i 改变到另一个偶(奇)数位置 p_j,不妨设 p_i < p_j,那么一定 \exists k \in \mathbb{N}^* 使得 p_i + 2k = p_j 成立,即此时的最小开销为 0。
- 从某一个偶(奇)数位置 p_i 改变到另一个奇(偶)数位置 p_j,不妨设 p_i < p_j,那么一定 \exists k \in \mathbb{N 使得 p_i + 2k + 1 = p_j 成立,即此时的最小开销为 1。
那么我们可以把初始每一个偶数位置的「筹码」看作一个整体,每一个奇数位置的「筹码」看作一个整体。因为我们的目标是最后将全部的「筹码」移动到同一个位置,那么最后的位置只有两种情况:
- 移动到某一个偶数位置,此时的开销最小值就是初始奇数位置「筹码」的数量。
- 移动到某一个奇数位置,此时的开销最小值就是初始偶数位置「筹码」的数量。
那么这两种情况中的最小值就是最后将所有筹码移动到同一位置上所需要的最小代价。
代码
1 | class Solution: |
1 | class Solution { |
1 | class Solution { |
1 | public class Solution { |
1 |
|
1 | var minCostToMoveChips = function(position) { |
1 | func minCostToMoveChips(position []int) int { |
复杂度分析
时间复杂度:O(n),其中 n 为数组 position 的长度,只对数组进行了一次遍历。
空间复杂度:O(1),仅使用常数变量。
Comments