1240-铺瓷砖
你是一位施工队的工长,根据设计师的要求准备为一套设计风格独特的房子进行室内装修。
房子的客厅大小为 n x m,为保持极简的风格,需要使用尽可能少的 正方形 瓷砖来铺盖地面。
假设正方形瓷砖的规格不限,边长都是整数。
请你帮设计师计算一下,最少需要用到多少块方形瓷砖?
示例 1:
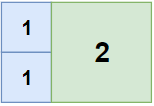
**输入:** n = 2, m = 3
**输出:** 3
**解释:** 3 块地砖就可以铺满卧室。
2 块 1x1 地砖
1 块 2x2 地砖
示例 2:
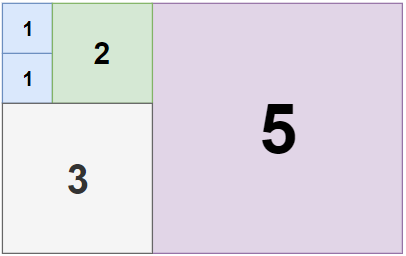
**输入:** n = 5, m = 8
**输出:** 5
示例 3:
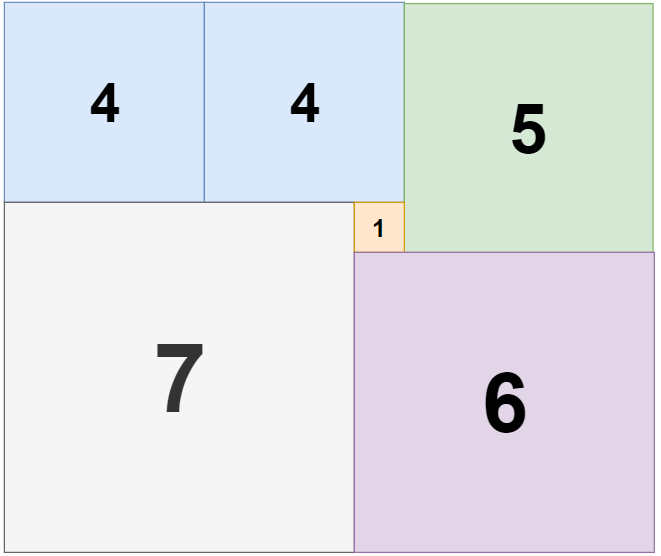
**输入:** n = 11, m = 13
**输出:** 6
提示:
1 <= n <= 131 <= m <= 13
方法一:回溯
前言
本题为一道经典的数学问题,详细可以参考相关的学术论文:「Minimum tiling of a rectangle by squares 」。假设 n,m 分别为矩形的长与宽,设 h(m,n) 表示铺满该矩形所需的正方形的最少数目,根据参考资料: 「Filling rectangles with integer-sided squares 」,已有如下结论:
- h(n,m) \le \max(n, m);
- h(n + m,m) = 1 + h(n, m) \quad \text{if} ~~ 1 \le m \le 4;
- h(n+m,m) = 1 + h(n,m) \quad \text{if} ~~ 3n \geq m^2;
详细证明过程参考相关学术论文即可,在此不再描述。
根据参考资料可以知道,实际该问题可以参考已有的计算结果与代码如下:
思路与算法
由于本题为 NP-Complete 问题,没有类似于动态规划的递推公式。具体到本题给定的 n,m 的取值范围为 1 \le n \le 13, 1 \le m \le 13,因此我们可以采用暴力搜索的方法,依次尝试在空余的格子中铺设正方形,尝试遍历所有可能铺设方法,找到最少的正方形的数目即可。我们用二维矩阵 rect}[n][m] 来表示当前长方形中每个点被覆盖的情况,具体搜索过程如下:
- 初始时,由于长方形的每个点均未被覆盖,矩阵中每个单元格的状态均设置为 false;
- 从位置 (0,0) 开始依次尝试用正方形来覆盖部分区域,如果当前位置 (x, y) 已经覆盖,则尝试下一个位置 (x, y + 1)。每次尝试从 (x, y) 进行正方形覆盖,假设当前覆盖的正方形的左上顶点为 (x,y),正方形的长度为 k,则过程如下:
- 由于当前覆盖的正方形不能超越长方形区域的边界,此时 k 的取值范围为 1 \le k < \min(n - x, m - y),为了减枝,k 的取值依次从大到小进行尝试。
- 同时需要检测该正方形区域内是否已被其它正方形覆盖过,即检测该区域中是否存在 rect}[i][j] = \text{true,此时 i,j 的取值范围 x \le i < x + k, y \le j < y + k,如果可以填充则对该正方形区域进行填充,并移动到下一个位置 (x, y + k) 继续尝试搜索;
- 当前如果已经将该矩形进行完全覆盖完成,记录当前最小值并返回。在搜索时同时对当前已经覆盖的正方形进行计数,如果当前计数 cnt 大于等于当前的最小值 ans 时,说明当前的覆盖方法已经不是最优解则直接返回。
代码
1 | class Solution { |
1 | class Solution { |
1 | public class Solution { |
1 | func min(a, b int) int { |
1 | bool isAvailable(const bool **rect, int x, int y, int k) { |
1 | var tilingRectangle = function(n, m) { |
1 | class Solution: |
复杂度分析
本题暂不分析时空复杂度。