1292-元素和小于等于阈值的正方形的最大边长

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:25 2023-09-13 16:06:25 Updated    

给你一个大小为 m x n 的矩阵 mat 和一个整数阈值 threshold。

请你返回元素总和小于或等于阈值的正方形区域的最大边长；如果没有这样的正方形区域，则返回 **0 **。

示例 1：

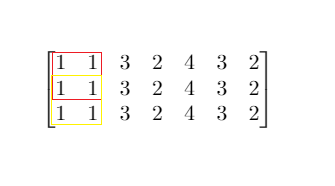
**输入：** mat = [[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]], threshold = 4
**输出：** 2
**解释：** 总和小于或等于 4 的正方形的最大边长为 2，如图所示。

示例 2：

**输入：** mat = [[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2]], threshold = 1
**输出：** 0

提示：

  • m == mat.length
  • n == mat[i].length
  • 1 <= m, n <= 300
  • 0 <= mat[i][j] <= 104
  • 0 <= threshold <= 105

预备知识

本题需要用到一些二维前缀和（Prefix Sum）的知识，它是一维前缀和的延伸：

设二维数组 A 的大小为 m * n，行下标的范围为 [1, m]，列下标的范围为 [1, n]。

数组 P 是 A 的前缀和数组，等价于 P 中的每个元素 P[i][j]：

  • 如果 i 和 j 均大于 0，那么 P[i][j] 表示 A 中以 (1, 1) 为左上角，(i, j) 为右下角的矩形区域的元素之和；

  • 如果 i 和 j 中至少有一个等于 0，那么 P[i][j] 也等于 0。

数组 P 可以帮助我们在 O(1) 的时间内求出任意一个矩形区域的元素之和。具体地，设我们需要求和的矩形区域的左上角为 (x1, y1)，右下角为 (x2, y2)，则该矩形区域的元素之和可以表示为：

1
2
sum = A[x1..x2][y1..y2]
    = P[x2][y2] - P[x1 - 1][y2] - P[x2][y1 - 1] + P[x1 - 1][y1 - 1]

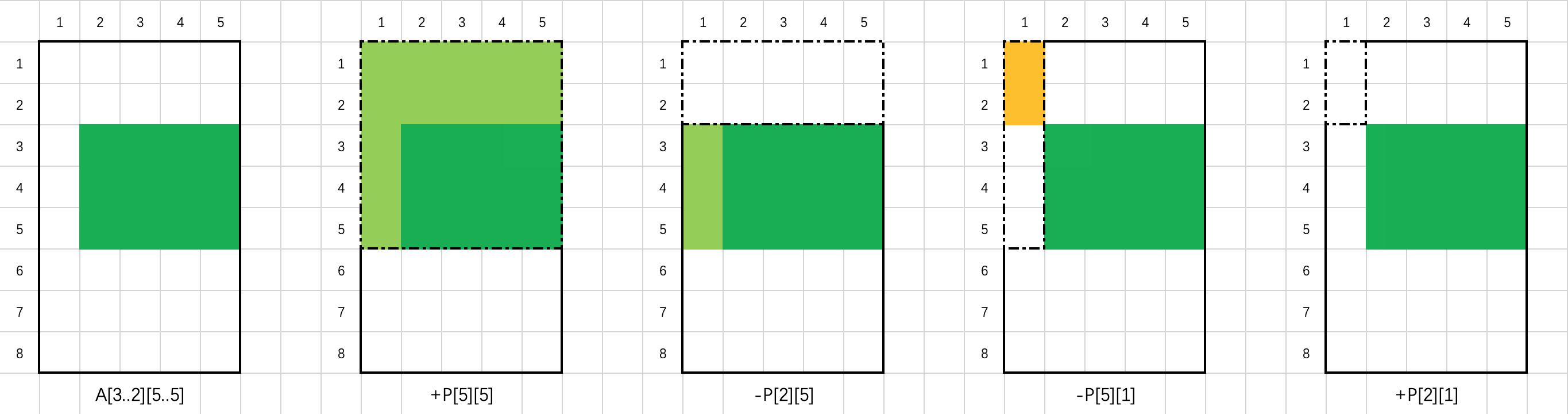
其正确性可以通过容斥原理得出。以下图为例，当 A 的大小为 8 * 5，需要求和的矩形区域（深绿色部分）的左上角为 (3, 2)，右下角为 (5, 5) 时，该矩形区域的元素之和为 P[5][5] - P[2][5] - P[5][1] + P[2][1]。

1292-1{:width=600}

那么如何得到数组 P 呢？我们按照行优先的顺序依次计算数组 P 中的每个元素，即当我们在计算 P[i][j] 时，数组 P 的前 i - 1 行，以及第 i 行的前 j - 1 个元素都已经计算完成。此时我们可以考虑 (i, j) 这个 1 * 1 的矩形区域，根据上面的等式，有：

1
A[i][j] = P[i][j] - P[i - 1][j] - P[i][j - 1] + P[i - 1][j - 1]

由于等式中的 A[i][j]，P[i - 1][j]，P[i][j - 1] 和 P[i - 1][j - 1] 均已知，我们可以通过：

1
P[i][j] = P[i - 1][j] + P[i][j - 1] - P[i - 1][j - 1] + A[i][j]

在 O(1) 的时间计算出 P[i][j]。因此按照行优先的顺序，我们可以在 O(MN) 的时间得到数组 P。在此之后，我们就可以很方便地在 O(1) 的时间内求出任意一个矩形区域的元素之和了。

注意事项：

在大部分语言中，数组下标是从 0 而不是 1 开始，在实际的代码编写过程中需要考虑这一情况。

方法一：二分查找

我们首先计算出数组 mat 的前缀和数组 P，随后依次枚举 mat 中的正方形，计算出每个正方形的元素之和。具体地，当数组 mat 的大小为 m * n 时，正方形的左上角可以是 mat 中的任意位置，边长不会超过 m 和 n 中的较小值 min(m, n)，这样我们就可以使用三重循环枚举所有的正方形，时间复杂度为 O(MN * \min(M, N))。由于我们可以借助数组 P 在 O(1) 的时间计算任意正方形的元素之和，因此该算法的总时间复杂度为 O(MN * \min(M, N))。

若使用 C++ 语言编写上述算法，则可以恰好在规定时间内通过所有测试数据，但对于 Python 语言则无法通过。因此我们必须对该算法进行优化。

由于数组 mat 中的所有元素均为非负整数，因此若存在一个边长为 c 且元素之和不超过阈值的正方形，那一定存在一个边长为 1, 2, ..., c - 1 且元素之和不超过阈值的正方形（在边长为 c 的正方形内任取一个边长为 1, 2, ..., c - 1 的正方形即可）。这样我们可以使用二分查找的方法，找出最大的边长 c。二分查找的上界为 min(m, n)，下界为 1，在二分查找的过程中，若当前查找的边长为 c'，我们只需要枚举 mat 中所有边长为 c' 的正方形，并判断其中是否存在一个元素之和不超过阈值的正方形即可。

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
public:
    int getRect(const vector<vector<int>>& P, int x1, int y1, int x2, int y2) {
        return P[x2][y2] - P[x1 - 1][y2] - P[x2][y1 - 1] + P[x1 - 1][y1 - 1];
    }

    int maxSideLength(vector<vector<int>>& mat, int threshold) {
        int m = mat.size(), n = mat[0].size();
        vector<vector<int>> P(m + 1, vector<int>(n + 1));
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                P[i][j] = P[i - 1][j] + P[i][j - 1] - P[i - 1][j - 1] + mat[i - 1][j - 1];
            }
        }

        int l = 1, r = min(m, n), ans = 0;
        while (l <= r) {
            int mid = (l + r) / 2;
            bool find = false;
            for (int i = 1; i <= m - mid + 1; ++i) {
                for (int j = 1; j <= n - mid + 1; ++j) {
                    if (getRect(P, i, j, i + mid - 1, j + mid - 1) <= threshold) {
                        find = true;
                    }
                }
            }
            if (find) {
                ans = mid;
                l = mid + 1;
            }
            else {
                r = mid - 1;
            }
        }
        return ans;
    }
};
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution:
    def maxSideLength(self, mat: List[List[int]], threshold: int) -> int:
        m, n = len(mat), len(mat[0])
        P = [[0] * (n + 1) for _ in range(m + 1)]
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                P[i][j] = P[i - 1][j] + P[i][j - 1] - P[i - 1][j - 1] + mat[i - 1][j - 1]
        
        def getRect(x1, y1, x2, y2):
            return P[x2][y2] - P[x1 - 1][y2] - P[x2][y1 - 1] + P[x1 - 1][y1 - 1]
        
        l, r, ans = 1, min(m, n), 0
        while l <= r:
            mid = (l + r) // 2
            find = any(getRect(i, j, i + mid - 1, j + mid - 1) <= threshold for i in range(1, m - mid + 2) for j in range(1, n - mid + 2))
            if find:
                ans = mid
                l = mid + 1
            else:
                r = mid - 1
        return ans

复杂度分析

  • 时间复杂度：O(MN * \log\min(M, N))。二分查找的次数为 O(\log\min(M, N))，在每次二分查找中，需要枚举所有边长为 c' 的矩形，数量为 O(MN)，因此总时间复杂度为 O(MN * \log\min(M, N))。

  • 空间复杂度：O(MN)。

方法二：枚举 + 优化

在方法一中，我们使用二分查找的方法，将时间复杂度为 O(MN * \min(M, N)) 的枚举算法优化至 O(MN * \log \min(M, N))。那么我们还可以继续优化下去吗？

我们舍弃二分查找的思路，转而想一想如何直接对枚举算法进行优化。枚举算法中包括三重循环，其中前两重循环枚举正方形的左上角位置，似乎没有什么优化的空间；而第三重循环枚举的是正方形的边长，对此我们很容易想到两个优化的思路：

  • 如果边长为 c 的正方形的元素之和已经超过阈值，那么我们就没有必要枚举更大的边长了。这是因为数组 mat 中的所有元素均为非负整数，如果固定了左上角的位置 (i, j)（即前两重循环），那么随着边长的增大，正方形的元素之和也会增大。

  • 由于我们的目标是找到边长最大的正方形，那么如果我们在前两重循环枚举到 (i, j) 之前已经找到了一个边长为 c' 的正方形，那么在枚举以 (i, j) 为左上角的正方形时，我们可以忽略所有边长小于等于 c' 的正方形，直接从 c' + 1 开始枚举。

基于上述的两个优化，我们可以编写出如下的代码：

[sol2-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    int getRect(const vector<vector<int>>& P, int x1, int y1, int x2, int y2) {
        return P[x2][y2] - P[x1 - 1][y2] - P[x2][y1 - 1] + P[x1 - 1][y1 - 1];
    }

    int maxSideLength(vector<vector<int>>& mat, int threshold) {
        int m = mat.size(), n = mat[0].size();
        vector<vector<int>> P(m + 1, vector<int>(n + 1));
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                P[i][j] = P[i - 1][j] + P[i][j - 1] - P[i - 1][j - 1] + mat[i - 1][j - 1];
            }
        }

        int r = min(m, n), ans = 0;
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                for (int c = ans + 1; c <= r; ++c) {
                    if (i + c - 1 <= m && j + c - 1 <= n && getRect(P, i, j, i + c - 1, j + c - 1) <= threshold) {
                        ++ans;
                    }
                    else {
                        break;
                    }
                }
            }
        }
        return ans;
    }
};
[sol2-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution:
    def maxSideLength(self, mat: List[List[int]], threshold: int) -> int:
        m, n = len(mat), len(mat[0])
        P = [[0] * (n + 1) for _ in range(m + 1)]
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                P[i][j] = P[i - 1][j] + P[i][j - 1] - P[i - 1][j - 1] + mat[i - 1][j - 1]
        
        def getRect(x1, y1, x2, y2):
            return P[x2][y2] - P[x1 - 1][y2] - P[x2][y1 - 1] + P[x1 - 1][y1 - 1]
        
        r, ans = min(m, n), 0
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                for c in range(ans + 1, r + 1):
                    if i + c - 1 <= m and j + c - 1 <= n and getRect(i, j, i + c - 1, j + c - 1) <= threshold:
                        ans += 1
                    else:
                        break
        return ans

优化后的算法时间复杂度是多少呢？显然，它等于第三重循环中边长 c 被枚举的次数。由于优化后第三重循环的上下界并不固定，因此我们需要使用一些技巧，将第三重循环中边长 c 的枚举分为两类：

  • 成功枚举：如果当前枚举的边长为 c 的正方形的元素之和不超过阈值，那么称此为一次「成功枚举」。在进行成功枚举后，我们找到了比之前边长更大的正方形。

  • 失败枚举：如果当前枚举的边长为 c 的正方形的元素之和大于阈值，那么称此为一次「失败枚举」。在进行失败枚举后，我们就没有必要枚举更大的边长了，会直接跳出第三重循环。

对于「成功枚举」而言，由于每进行一次「成功枚举」，我们都会得到一个边长更大的正方形，而边长的最大值不会超过 min(m, n)，因此「成功枚举」的总次数也不会超过 min(m, n)；对于「失败枚举」而言，由于每进行一次「失败枚举」，都会直接跳出第三重循环，因此每一个左上角的位置 (i, j) 最多只会对应一次「失败枚举」，即「失败枚举」的总次数不会超过 mn。因此，优化后算法的时间复杂度为 O(\min(M, N) + MN) = O(MN)，它比二分查找更优。

复杂度分析

  • 时间复杂度：O(MN)。这看上去很不可思议，但它确实比方法一中二分查找的时间复杂度更低。

  • 空间复杂度：O(MN)。

 Comments
On this page
1292-元素和小于等于阈值的正方形的最大边长