给你 root1 和 root2 这两棵二叉搜索树。请你返回一个列表,其中包含 **两棵树 **中的所有整数并按 升序 排序。.
示例 1:
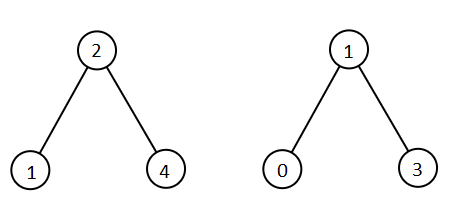
**输入:** root1 = [2,1,4], root2 = [1,0,3]
**输出:** [0,1,1,2,3,4]
示例 2:
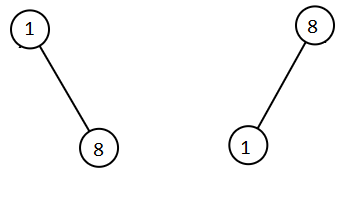
**输入:** root1 = [1,null,8], root2 = [8,1]
**输出:** [1,1,8,8]
提示:
- 每棵树的节点数在
[0, 5000] 范围内
-105 <= Node.val <= 105
方法一:中序遍历 + 归并
回顾二叉搜索树的定义:
- 当前节点的左子树中的数均小于当前节点的数;
- 当前节点的右子树中的数均大于当前节点的数;
- 所有左子树和右子树自身也是二叉搜索树。
根据上述定义,我们可以用中序遍历访问二叉搜索树,即按照访问左子树——根节点——右子树的方式遍历这棵树,而在访问左子树或者右子树的时候也按照同样的方式遍历,直到遍历完整棵树。遍历结束后,就得到了一个有序数组。
由于整个遍历过程天然具有递归的性质,我们可以直接用递归函数来模拟这一过程。具体描述见 94. 二叉树的中序遍历 的 官方题解 。
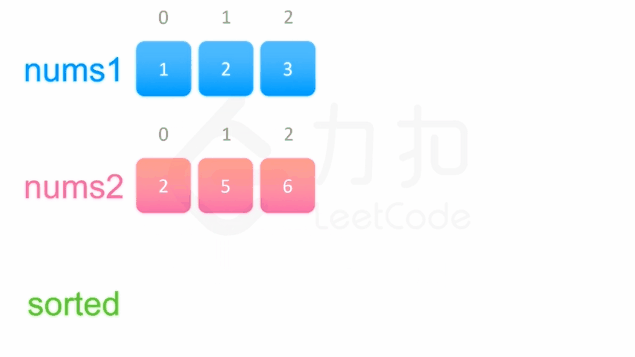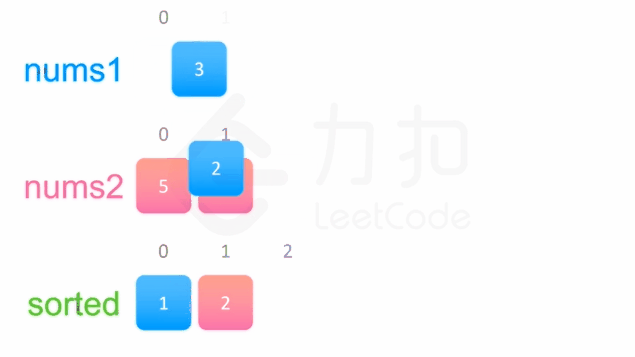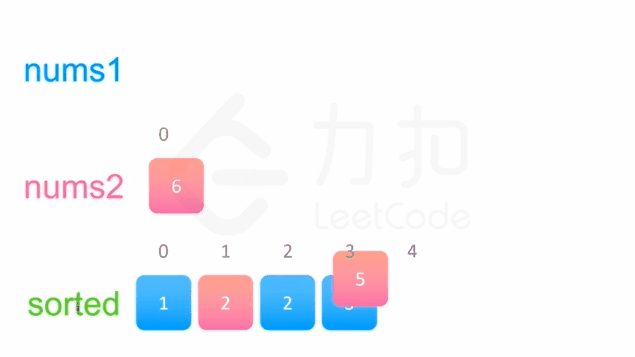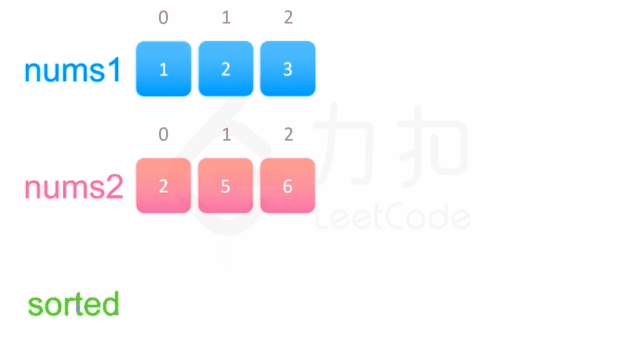
中序遍历这两棵二叉搜索树,可以得到两个有序数组。然后可以使用双指针方法来合并这两个有序数组,这一方法将两个数组看作两个队列,每次从队列头部取出比较小的数字放到结果中(头部相同时可任取一个)。如下面的动画所示:
 {:width=540}
{:width=540}
[sol1-Python3]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| class Solution:
def getAllElements(self, root1: TreeNode, root2: TreeNode) -> List[int]:
def inorder(node: TreeNode, res: List[int]):
if node:
inorder(node.left, res)
res.append(node.val)
inorder(node.right, res)
nums1, nums2 = [], []
inorder(root1, nums1)
inorder(root2, nums2)
merged = []
p1, n1 = 0, len(nums1)
p2, n2 = 0, len(nums2)
while True:
if p1 == n1:
merged.extend(nums2[p2:])
break
if p2 == n2:
merged.extend(nums1[p1:])
break
if nums1[p1] < nums2[p2]:
merged.append(nums1[p1])
p1 += 1
else:
merged.append(nums2[p2])
p2 += 1
return merged
|
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| class Solution {
void inorder(TreeNode *node, vector<int> &res) {
if (node) {
inorder(node->left, res);
res.push_back(node->val);
inorder(node->right, res);
}
}
public:
vector<int> getAllElements(TreeNode *root1, TreeNode *root2) {
vector<int> nums1, nums2;
inorder(root1, nums1);
inorder(root2, nums2);
vector<int> merged;
auto p1 = nums1.begin(), p2 = nums2.begin();
while (true) {
if (p1 == nums1.end()) {
merged.insert(merged.end(), p2, nums2.end());
break;
}
if (p2 == nums2.end()) {
merged.insert(merged.end(), p1, nums1.end());
break;
}
if (*p1 < *p2) {
merged.push_back(*p1++);
} else {
merged.push_back(*p2++);
}
}
return merged;
}
};
|
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| class Solution {
public List<Integer> getAllElements(TreeNode root1, TreeNode root2) {
List<Integer> nums1 = new ArrayList<Integer>();
List<Integer> nums2 = new ArrayList<Integer>();
inorder(root1, nums1);
inorder(root2, nums2);
List<Integer> merged = new ArrayList<Integer>();
int p1 = 0, p2 = 0;
while (true) {
if (p1 == nums1.size()) {
merged.addAll(nums2.subList(p2, nums2.size()));
break;
}
if (p2 == nums2.size()) {
merged.addAll(nums1.subList(p1, nums1.size()));
break;
}
if (nums1.get(p1) < nums2.get(p2)) {
merged.add(nums1.get(p1++));
} else {
merged.add(nums2.get(p2++));
}
}
return merged;
}
public void inorder(TreeNode node, List<Integer> res) {
if (node != null) {
inorder(node.left, res);
res.add(node.val);
inorder(node.right, res);
}
}
}
|
[sol1-C#]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| public class Solution {
public IList<int> GetAllElements(TreeNode root1, TreeNode root2) {
IList<int> nums1 = new List<int>();
IList<int> nums2 = new List<int>();
Inorder(root1, nums1);
Inorder(root2, nums2);
IList<int> merged = new List<int>();
int p1 = 0, p2 = 0;
while (true) {
if (p1 == nums1.Count) {
while (p2 < nums2.Count) {
merged.Add(nums2[p2++]);
}
break;
}
if (p2 == nums2.Count) {
while (p1 < nums1.Count) {
merged.Add(nums1[p1++]);
}
break;
}
if (nums1[p1] < nums2[p2]) {
merged.Add(nums1[p1++]);
} else {
merged.Add(nums2[p2++]);
}
}
return merged;
}
public void Inorder(TreeNode node, IList<int> res) {
if (node != null) {
Inorder(node.left, res);
res.Add(node.val);
Inorder(node.right, res);
}
}
}
|
[sol1-Golang]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| func inorder(root *TreeNode) (res []int) {
var dfs func(*TreeNode)
dfs = func(node *TreeNode) {
if node == nil {
return
}
dfs(node.Left)
res = append(res, node.Val)
dfs(node.Right)
}
dfs(root)
return
}
func getAllElements(root1, root2 *TreeNode) []int {
nums1 := inorder(root1)
nums2 := inorder(root2)
p1, n1 := 0, len(nums1)
p2, n2 := 0, len(nums2)
merged := make([]int, 0, n1+n2)
for {
if p1 == n1 {
return append(merged, nums2[p2:]...)
}
if p2 == n2 {
return append(merged, nums1[p1:]...)
}
if nums1[p1] < nums2[p2] {
merged = append(merged, nums1[p1])
p1++
} else {
merged = append(merged, nums2[p2])
p2++
}
}
}
|
[sol1-C]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| #define MAX_NODE_SIZE 5001
void inorder(struct TreeNode *node, int *res, int *pos) {
if (node) {
inorder(node->left, res, pos);
res[(*pos)++] = node->val;
inorder(node->right, res, pos);
}
}
int* getAllElements(struct TreeNode* root1, struct TreeNode* root2, int* returnSize) {
int *nums1 = (int *)malloc(sizeof(int) * MAX_NODE_SIZE);
int *nums2 = (int *)malloc(sizeof(int) * MAX_NODE_SIZE);
int pos1 = 0, pos2 = 0;
inorder(root1, nums1, &pos1);
inorder(root2, nums2, &pos2);
int *merged = (int *)malloc(sizeof(int) * (pos1 + pos2));
int p1 = 0, p2 = 0;
int pos = 0;
while (true) {
if (p1 == pos1) {
memcpy(merged + pos, nums2 + p2, sizeof(int) * (pos2 - p2));
break;
}
if (p2 == pos2) {
memcpy(merged + pos, nums1 + p1, sizeof(int) * (pos1 - p1));
break;
}
if (nums1[p1] < nums2[p2]) {
merged[pos++] = nums1[p1++];
} else {
merged[pos++] = nums2[p2++];
}
}
*returnSize = pos1 + pos2;
return merged;
}
|
[sol1-JavaScript]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| var getAllElements = function(root1, root2) {
const nums1 = [];
const nums2 = [];
const inorder = (node, res) => {
if (node) {
inorder(node.left, res);
res.push(node.val);
inorder(node.right, res);
}
};
inorder(root1, nums1);
inorder(root2, nums2);
const merged = [];
let p1 = 0, p2 = 0;
while (true) {
if (p1 === nums1.length) {
for (let i = p2; i < nums2.length; i++) {
merged.push(nums2[i]);
}
break;
}
if (p2 === nums2.length) {
for (let i = p1; i < nums1.length;i++) {
merged.push(nums1[i]);
}
break;
}
if (nums1[p1] < nums2[p2]) {
merged.push(nums1[p1++]);
} else {
merged.push(nums2[p2++]);
}
}
return merged;
}
|
复杂度分析
 {:width=540}
{:width=540}