1325-删除给定值的叶子节点

给你一棵以 root 为根的二叉树和一个整数 target ，请你删除所有值为 target 的 叶子节点 。

注意，一旦删除值为 target 的叶子节点，它的父节点就可能变成叶子节点；如果新叶子节点的值恰好也是 target ，那么这个节点也应该被删除。

也就是说，你需要重复此过程直到不能继续删除。

示例 1：

![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/01/16/sample_1_1684.png)

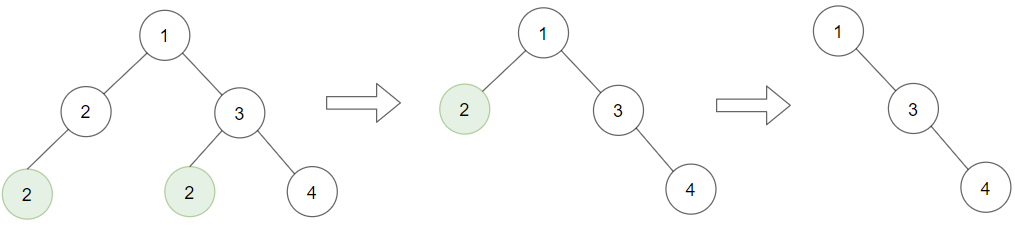
**输入：** root = [1,2,3,2,null,2,4], target = 2
**输出：** [1,null,3,null,4]
**解释：** 上面左边的图中，绿色节点为叶子节点，且它们的值与 target 相同（同为 2 ），它们会被删除，得到中间的图。
有一个新的节点变成了叶子节点且它的值与 target 相同，所以将再次进行删除，从而得到最右边的图。

示例 2：

![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/01/16/sample_2_1684.png)

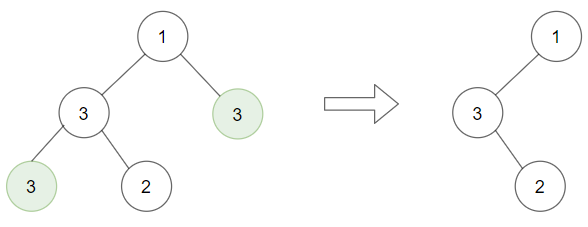
**输入：** root = [1,3,3,3,2], target = 3
**输出：** [1,3,null,null,2]

示例 3：

![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/01/16/sample_3_1684.png)

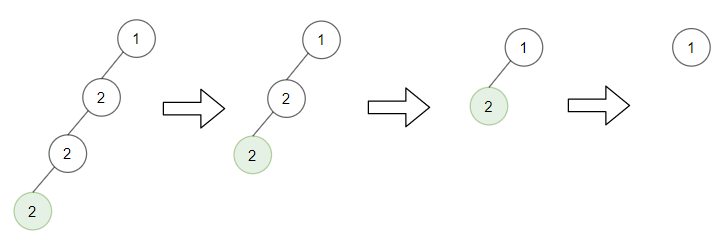
**输入：** root = [1,2,null,2,null,2], target = 2
**输出：** [1]
**解释：** 每一步都删除一个绿色的叶子节点（值为 2）。

示例 4：

**输入：** root = [1,1,1], target = 1
**输出：** []

示例 5：

**输入：** root = [1,2,3], target = 1
**输出：** [1,2,3]

提示：

• 1 <= target <= 1000
• 每一棵树最多有 3000 个节点。
• 每一个节点值的范围是 [1, 1000] 。

方法一：递归

由于我们需要删除所有值为 target 的叶子节点，那么我们的操作顺序应当从二叉树的叶子节点开始，逐步向上直到二叉树的根为止。因此我们可以使用递归的方法遍历整颗二叉树，并在回溯时进行删除操作。这样对于二叉树中的每个节点，它的子节点一定先于它被操作。这其实也就是二叉树的后序遍历。

具体地，当我们回溯到某个节点 u 时，如果 u 的左右孩子均不存在（这里有两种情况，一是节点 u 的孩子本来就不存在，二是节点 u 的孩子变成了叶子节点并且值为 target，导致其被删除），并且值为 target，那么我们要删除节点 u，递归函数的返回值为空节点；如果节点 u 不需要被删除，那么递归函数的返回值为节点 u 本身。

[sol1-C++]

class Solution {
public:
    TreeNode* removeLeafNodes(TreeNode* root, int target) {
        if (!root) {
            return nullptr;
        }
        root->left = removeLeafNodes(root->left, target);
        root->right = removeLeafNodes(root->right, target);
        if (!root->left && !root->right && root->val == target) {
            return nullptr;
        }
        return root;
    }
};

[sol1-Python3]

class Solution:
    def removeLeafNodes(self, root: TreeNode, target: int) -> TreeNode:
        if not root:
            return None
        root.left = self.removeLeafNodes(root.left, target)
        root.right = self.removeLeafNodes(root.right, target)
        if not root.left and not root.right and root.val == target:
            return None
        return root

复杂度分析

• 时间复杂度：O(N)，其中 N 是二叉树的节点个数。

• 空间复杂度：O(H)，其中 H 是二叉树的高度。