1334-阈值距离内邻居最少的城市

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 11:01:41 2023-09-13 11:01:41 Updated    

有 n 个城市，按从 0 到 n-1 编号。给你一个边数组 edges，其中 edges[i] = [fromi, toi, weighti] 代表 fromi 和 toi 两个城市之间的双向加权边，距离阈值是一个整数 distanceThreshold。

返回能通过某些路径到达其他城市数目最少、且路径距离 最大 为 distanceThreshold
的城市。如果有多个这样的城市，则返回编号最大的城市。

注意，连接城市 i 和 j 的路径的距离等于沿该路径的所有边的权重之和。

示例 1：

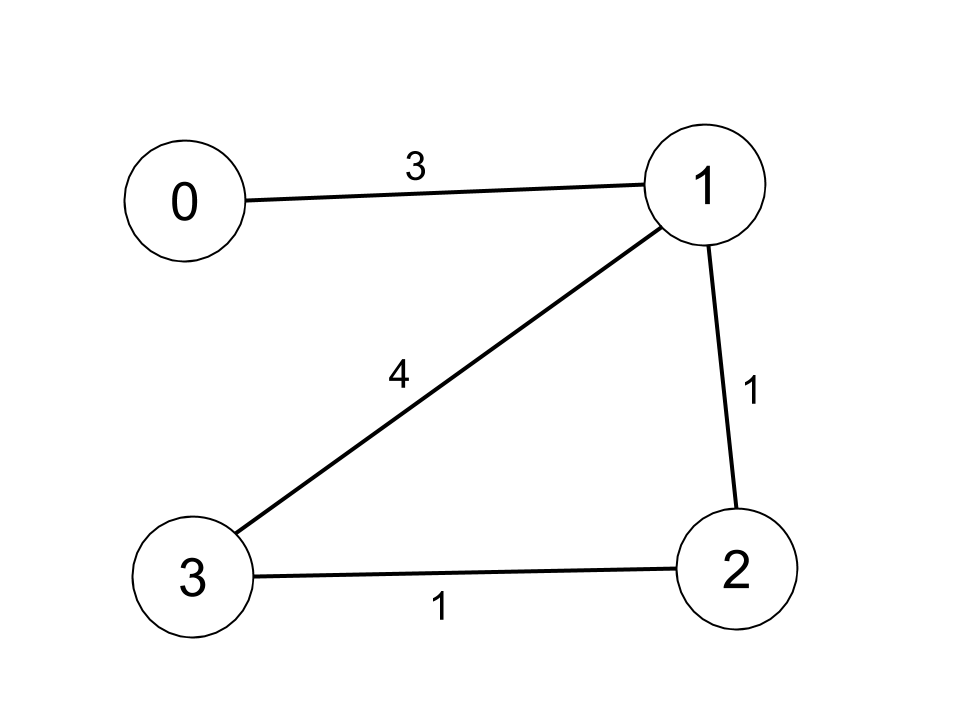
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/01/26/find_the_city_01.png)

**输入：** n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
**输出：** 3
**解释：** 城市分布图如上。
每个城市阈值距离 distanceThreshold = 4 内的邻居城市分别是：
城市 0 -> [城市 1, 城市 2] 
城市 1 -> [城市 0, 城市 2, 城市 3] 
城市 2 -> [城市 0, 城市 1, 城市 3] 
城市 3 -> [城市 1, 城市 2] 
城市 0 和 3 在阈值距离 4 以内都有 2 个邻居城市，但是我们必须返回城市 3，因为它的编号最大。

示例 2：

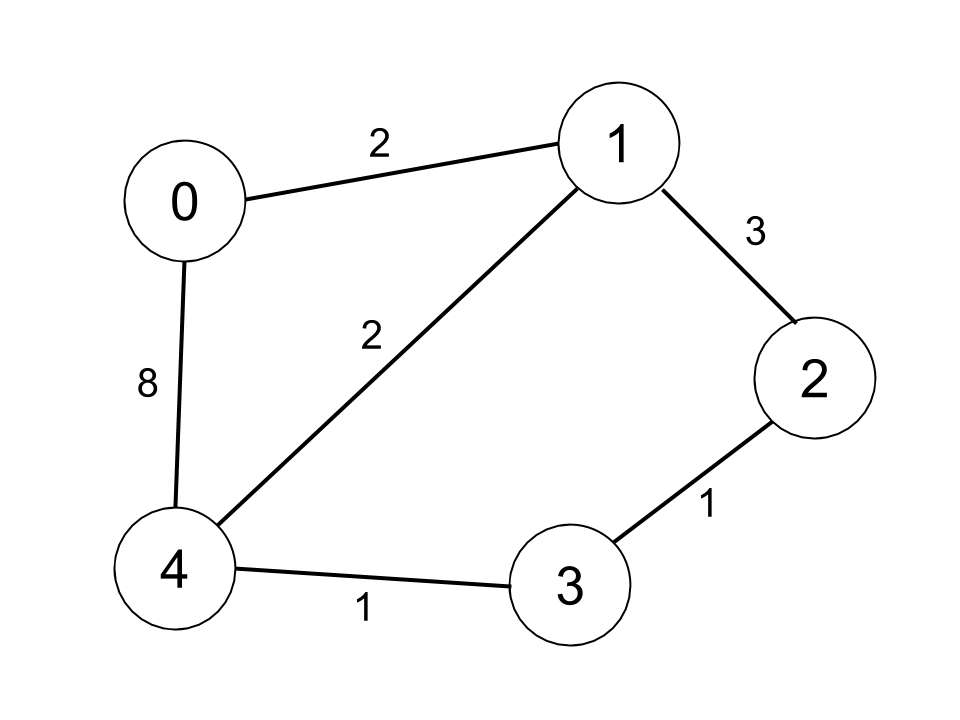
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/01/26/find_the_city_02.png)

**输入：** n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
**输出：** 0
**解释：** 城市分布图如上。 
每个城市阈值距离 distanceThreshold = 2 内的邻居城市分别是：
城市 0 -> [城市 1] 
城市 1 -> [城市 0, 城市 4] 
城市 2 -> [城市 3, 城市 4] 
城市 3 -> [城市 2, 城市 4]
城市 4 -> [城市 1, 城市 2, 城市 3] 
城市 0 在阈值距离 2 以内只有 1 个邻居城市。

提示：

  • 2 <= n <= 100
  • 1 <= edges.length <= n * (n - 1) / 2
  • edges[i].length == 3
  • 0 <= fromi < toi < n
  • 1 <= weighti, distanceThreshold <= 10^4
  • 所有 (fromi, toi) 都是不同的。

解题思路

单源最短路径问题：Dijkstra、Bellman-Ford、SPFA
全源最短路径问题：Floyd

模板参考：《算法笔记》

所有算法代码附有本题执行结果图片，读者可以自行比对。

方法一：Floyd

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
public:
    void Floyd(vector<vector<int>>& distances, int n){
        for (int k=0; k<n; ++k) {
            for (int i=0; i<n; ++i) {
                for (int j=0; j<n; ++j) {
                    if (distances[i][k]!=INT_MAX && distances[k][j] != INT_MAX && distances[i][k] + distances[k][j] < distances[i][j]) {
                        distances[i][j] = distances[i][k] + distances[k][j];
                    }
                }
            }
        }
    }
    int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
        vector<vector<int>>distances(n,vector<int>(n,INT_MAX)); //全源最短路径矩阵
        for (int i=0; i<n; i++) {
            distances[i][i] = 0; //自身到自身的距离为0
        }
        for (vector<int> edge : edges) {
            int u=edge[0], v=edge[1], w=edge[2];
            distances[u][v]=w;
            distances[v][u]=w;
        }
        Floyd(distances, n);
        int idx = -1, minCount = INT_MAX;
        for (int i=0; i<n; ++i) {
            int count = 0;
            for (int j=0; j<n; ++j) {
                if (distances[i][j]<=distanceThreshold && i!=j) {
                    count++;
                }
            }
            if (count <= minCount) {
                minCount = count;
                idx = i;
            }
        }
        return idx;
    }
};

执行效率：

执行用时：84 ms, 在所有 C++ 提交中击败了64.89%的用户

内存消耗：12.2 MB, 在所有 C++ 提交中击败了28.24%的用户

Screen Shot 2021-07-15 at 12.30.34 PM.png

使用C静态数组可极大提速，也是本题的最优解：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
        const int INF = 0x3f3f3f3f;
        int dist[n][n];
        memset(dist,INF,sizeof(dist));
        for(int i=0;i<n;i++)
        dist[i][i]=0;
        for(int i=0;i<edges.size();i++){
            dist[edges[i][0]][edges[i][1]]=edges[i][2];
            dist[edges[i][1]][edges[i][0]]=edges[i][2];
        }
        for(int k=0;k<n;k++){
            for(int i=0;i<n;i++){
                for(int j=0;j<n;j++){
                    dist[i][j]=min(dist[i][j],dist[i][k]+dist[k][j]);
                }
            }
        }
        int id=-1, minCnt=INF;
        for(int i=0;i<n;i++){
            int cnt=0;
            for(int j=0;j<n;j++){
                if(dist[i][j]<=distanceThreshold)
                    cnt++;
            }
            if(cnt<=minCnt){
                minCnt=cnt;
                id=i;
            }
        }
        return id;
    }
};

执行效率：

执行用时：20 ms, 在所有 C++ 提交中击败了99.61%的用户

内存消耗：11.3 MB, 在所有 C++ 提交中击败了93.39%的用户

Screen Shot 2021-07-16 at 5.31.45 PM.png

方法二：Dijkstra
利用优先队列替换for循环是另一种写法，第二栏是priority_queue版，实测本题使用priority_queue运行速度反而下降。

邻接矩阵版：

[]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
public:
    void Dijkstra(vector<vector<int>>& graph, vector<int>& distances, vector<bool>& visited, int n, int distanceThreshold, int start) {
        distances[start] = 0; //自身到自身的距离为0
        for (int i=0; i<n; ++i) {
            int u=-1, minDis = INT_MAX;
            for (int j=0; j<n; ++j) {
                if (!visited[j] && distances[j] < minDis) {
                    u = j;
                    minDis = distances[j];
                }
            }
            if (u==-1) return; //所有点不可达
            visited[u] = true;
            for (int v=0; v<n; ++v) {
                if (!visited[v] && graph[u][v] != INT_MAX) {
                    if (distances[u] + graph[u][v] < distances[v]) {
                        distances[v] = distances[u] + graph[u][v];
                    }
                }
            }
        }
    }
    int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
        vector<vector<int>>graph(n,vector<int>(n,INT_MAX)); //邻接矩阵
        for (vector<int> edge : edges) {
            int u=edge[0], v=edge[1], w=edge[2];
            graph[u][v] = graph[v][u] = w;
        }
        int idx = -1, minCount = INT_MAX;
        for (int i=0; i<n; ++i) {
            vector<int>distances(n,INT_MAX); //单源最短路径数组
            vector<bool>visited(n,false);
            Dijkstra(graph, distances, visited, n, distanceThreshold, i);
            int count = 0; //小于等于距离阈值的城市个数
            for (int j=0; j<n; ++j) {
                if (distances[j]<=distanceThreshold && i!=j) {
                    count++;
                }
            }
            if (count <= minCount) {
                minCount = count;
                idx = i;
            }
        }
        return idx;
    }
};
[]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Solution { //优先队列版
public:
    void Dijkstra(vector<vector<int>>& graph, vector<int>& distances, int n, int distanceThreshold, int start) {
        //小顶堆，按照距离dist从小到大排序，pair中first存dist
        priority_queue <pair<int, int>,vector<pair<int, int>>, greater<pair<int, int>>> q;
        distances[start] = 0;
        q.push({distances[start],start});
        while (!q.empty()) {
            pair<int, int>p = q.top();
            int u = p.second;
            q.pop();
            if (distances[u] < p.first) {
                continue;
            }
            for (int v=0; v<n; ++v) {
                if (graph[u][v] != INT_MAX && distances[v]>distances[u]+graph[u][v]) {
                    distances[v]=distances[u]+graph[u][v];
                        q.push({distances[v],v});
                }
            }
        }
    }
    int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
        vector<vector<int>>graph(n,vector<int>(n,INT_MAX)); //邻接矩阵
        for (vector<int> edge : edges) {
            int u=edge[0], v=edge[1], w=edge[2];
            graph[u][v] = graph[v][u] = w;
        }
        int idx = -1, minCount = INT_MAX;
        for (int i=0; i<n; ++i) {
            vector<int>distances(n,INT_MAX); //单源最短路径数组
            Dijkstra(graph, distances, n, distanceThreshold, i);
            int count = 0; //小于等于距离阈值的城市个数
            for (int j=0; j<n; ++j) {
                if (distances[j]<=distanceThreshold && i!=j) {
                    count++;
                }
            }
            if (count <= minCount) {
                minCount = count;
                idx = i;
            }
        }
        return idx;
    }
};

执行效率：

执行用时：68 ms, 在所有 C++ 提交中击败了73.66%的用户

内存消耗：12.6 MB, 在所有 C++ 提交中击败了17.55%的用户

Screen Shot 2021-07-15 at 12.32.30 PM.png

使用静态数组可极大提速

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class Solution {
public:
    int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
        const int INF = 0x3f3f3f3f;
        int graph[n][n];
        memset(graph,INF,sizeof(graph));
        int dist[n];
        bool vis[n];
        for (vector<int> edge : edges) {
            int u=edge[0], v=edge[1], w=edge[2];
            graph[u][v] = graph[v][u] = w;
        }
        int idx = -1, minCnt = INF;
        for (int i=0; i<n; ++i) {
            memset(dist, INF, sizeof(dist));
            dist[i] = 0; //自身到自身的距离为0
            memset(vis, false, sizeof(vis));
            for (int j=0; j<n; ++j) {
                int u=-1, minDis = INF;
                for (int k=0; k<n; ++k) {
                    if (!vis[k] && dist[k] < minDis) {
                        u = k;
                        minDis = dist[k];
                    }
                }
                if (u==-1) {
                    break; //所有点不可达，直接结束，加速代码进程
                }
                vis[u] = true;
                for (int v=0; v<n; ++v) {
                    if (!vis[v]) {
                        dist[v] = min(dist[v], dist[u] + graph[u][v]);
                    }
                }
            }
            int cnt = 0;
            for (int j=0; j<n; ++j) {
                if (dist[j] <= distanceThreshold && i != j) {
                    cnt++;
                }
            }
            if (cnt <= minCnt) {
                minCnt = cnt;
                idx = i;
            }
        }
        return idx;
    }
};

执行效率：

执行用时：28 ms, 在所有 C++ 提交中击败了97.67%的用户

内存消耗：11.8 MB, 在所有 C++ 提交中击败了47.47%的用户

Screen Shot 2021-07-16 at 9.34.24 PM.png

邻接表版：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class Solution {
public:
    void Dijkstra(vector<vector<pair<int, int>>>&graph, vector<int>& distances, vector<bool>& visited, int n, int distanceThreshold, int start) {
        distances[start] = 0; //自身到自身的距离为0
        for (int i=0; i<n; ++i) {
            int u=-1, minDis = INT_MAX;
            for (int j=0; j<n; ++j) {
                if (!visited[j] && distances[j] < minDis) {
                    u = j;
                    minDis = distances[j];
                }
            }
            if (u==-1) return; //所有点不可达
            visited[u] = true;
            for (int j=0; j<graph[u].size(); ++j) {
                int v = graph[u][j].first;
                int w = graph[u][j].second;
                if (!visited[v]) {
                    if (distances[u] + w < distances[v]) {
                        distances[v] = distances[u] + w;
                    }
                }
            }
        }
    }
    int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
        vector<vector<pair<int, int>>>graph(n); //邻接表
        for (vector<int> edge : edges) {
            int u=edge[0], v=edge[1], w=edge[2];
            graph[u].push_back(make_pair(v, w));
            graph[v].push_back(make_pair(u, w));
        }
        int idx = -1, minCount = INT_MAX;
        for (int i=0; i<n; ++i) {
            vector<int>distances(n,INT_MAX); //单源最短路径数组
            vector<bool>visited(n,false);
            Dijkstra(graph, distances, visited, n, distanceThreshold, i);
            int count = 0; //小于等于距离阈值的城市个数
            for (int j=0; j<n; ++j) {
                if (distances[j]<=distanceThreshold && i!=j) {
                    count++;
                }
            }
            if (count <= minCount) {
                minCount = count;
                idx = i;
            }
        }
        return idx;
    }
};

执行效率：

执行用时：52 ms, 在所有 C++ 提交中击败了80.92%的用户

内存消耗：13.2 MB, 在所有 C++ 提交中击败了15.65%的用户

Screen Shot 2021-07-15 at 12.31.31 PM.png

方法三：Bellman-Ford

注意：
1.这里用到边表，但是不能直接用题目给的vector<vector>& edges，必须要自己构建vector& edges，Edge是结构体，否则会超时。
2.题目给的是无向边，每条无向边实际上是两条有向边，分析时注意。

Bellman-Ford可根据距离判断图有没有负环，本题无需判断负环，模板中舍去。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution {
public:
    struct Edge{
        int from;
        int to;
        int weight;
    };
    void BellmanFord(vector<Edge>& edges, vector<int>& distances, int n, int start) {
        distances[start] = 0;
        for(auto& e:edges){
            if(e.from == start) distances[e.to] = e.weight;
        }
        for(int i=0; i<n-1; ++i){
            for(auto& e:edges){
                if(distances[e.from] != INT_MAX && distances[e.to] > distances[e.from]+e.weight)
                    distances[e.to] = distances[e.from]+e.weight;
            }
        }
    }
    int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
        vector<Edge> evec;
        for (vector<int> e: edges) {
            Edge e1,e2;
            e1.from = e[0]; e1.to = e[1]; e1.weight = e[2];
            e2.from = e[1]; e2.to = e[0]; e2.weight = e[2];
            evec.emplace_back(e1); evec.emplace_back(e2);
        }
        int idx = -1, minCount = INT_MAX;
        for (int i=0; i<n; ++i) {
            vector<int>distances(n,INT_MAX); //单源最短路径数组
            BellmanFord(evec, distances, n, i);
            int count = 0; //小于等于距离阈值的城市个数
            for (int j=0; j<n; ++j) {
                if (distances[j]<=distanceThreshold && i!=j) {
                    count++;
                }
            }
            if (count <= minCount) {
                minCount = count;
                idx = i;
            }
        }
        return idx;
    }
};

执行效率：

执行用时：956 ms, 在所有 C++ 提交中击败了5.38%的用户

内存消耗：13 MB, 在所有 C++ 提交中击败了16.16%的用户

Screen Shot 2021-07-15 at 12.29.54 PM.png

方法四：SPFA
Bellman-Ford的优化，利用队列优化，队列升级为优先队列可进一步加速，有空更新SPFA的priority_queue加速版。
SPFA可根据顶点入队次数判断有没有负环，本题无需判断负环，模板中顶点入队次数数组舍去。

邻接表版(数组表示)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class Solution {
public:
    void SPFA(vector<vector<pair<int, int>>>& graph, vector<int>& distances, vector<bool>& inQueue, int start) {
        queue<int>q;
        q.push(start); //源点入队
        distances[start] = 0;
        inQueue[start] = true; //源点已入队
        while (!q.empty()) {
            int u = q.front();
            q.pop();
            inQueue[u] = false; //已出队
            for (int k=0; k<graph[u].size(); ++k) {
                int v = graph[u][k].first;
                int w = graph[u][k].second;
                if (distances[u] + w < distances[v]) {
                    distances[v] = distances[u] + w;
                    if (!inQueue[v]) {
                        q.push(v);
                        inQueue[v] = true;
                    }
                }
            }
        }
    }
    int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
        vector<vector<pair<int, int>>>graph(n); //邻接表
        for (vector<int> edge : edges) {
            int u=edge[0], v=edge[1], w=edge[2];
            graph[u].push_back(make_pair(v, w));
            graph[v].push_back(make_pair(u, w));
        }
        int idx = -1, minCount = INT_MAX;
        for (int i=0; i<n; ++i) {
            vector<int>distances(n,INT_MAX); //单源最短路径数组
            vector<bool>inQueue(n,false); //顶点是否在队列中
            SPFA(graph, distances, inQueue, i);
            int count = 0; //小于等于距离阈值的城市个数
            for (int j=0; j<n; ++j) {
                if (distances[j]<=distanceThreshold && i!=j) {
                    count++;
                }
            }
            if (count <= minCount) {
                minCount = count;
                idx = i;
            }
        }
        return idx;
    }
};

执行效率：

执行用时：72 ms, 在所有 C++ 提交中击败了61.68%的用户

内存消耗：14.3 MB, 在所有 C++ 提交中击败了16.60%的用户

Screen Shot 2021-07-29 at 9.52.59 PM.png

邻接表版(静态链表表示）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
class Solution {
    static constexpr int MAXN = 1100, MAXM = MAXN*(MAXN-1)/2;
public:
    struct Edge{
        int from;
        int to;
        int weight;
        int next;
    }e[MAXM];
    int head[MAXN];
    int t;
    void add(int u, int v, int w) {
        e[t].from = u;
        e[t].to = v;
        e[t].weight = w;
        e[t].next = head[u];
        head[u] = t++;
    }
    void SPFA(vector<int>& distances, vector<bool>& visited, int start) {
        queue<int>q;
        q.push(start);
        distances[start] = 0;
        while (!q.empty()) {
            int u = q.front();
            q.pop();
            visited[u] = false;
            for (int i=head[u]; i!=-1; i=e[i].next) {
                int v = e[i].to;
                if (distances[v]>distances[u]+e[i].weight) {
                    distances[v] = distances[u]+e[i].weight;
                    if (!visited[v]) {
                        visited[v] = true;
                        q.push(v);
                    }
                }
            }
        }
    }
    int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
        t = 0;
        memset(head, -1, sizeof(head));
        for (vector<int> e: edges) { //添加所有无向边
            add(e[0], e[1], e[2]);
            add(e[1], e[0], e[2]);
        }
        int idx = -1, minCount = INT_MAX;
        for (int i=0; i<n; ++i) {
            vector<int>distances(n,INT_MAX); //单源最短路径数组
            vector<bool>visited(n,false);
            SPFA(distances, visited, i);
            int count = 0; //小于等于距离阈值的城市个数
            for (int j=0; j<n; ++j) {
                if (distances[j]<=distanceThreshold && i!=j) {
                    count++;
                }
            }
            if (count <= minCount) {
                minCount = count;
                idx = i;
            }
        }
        return idx;
    }
};

执行效率：

执行用时：72 ms, 在所有 C++ 提交中击败了72.31%的用户

内存消耗：23.7 MB, 在所有 C++ 提交中击败了5.39%的用户

Screen Shot 2021-07-15 at 12.30.34 PM.png

总结

执行效率最高的是Floyd和Dijkstra：
在使用vector的情况下，Dijkstra快于Floyd；
在使用C静态数组的情况下，Floyd快于Dijkstra；
C静态数组大大快于vector。

执行效率最低的是Bellman-Ford。

吐血模板大总结，有空将持续更新，欢迎收藏点赞评论。

 Comments
On this page
1334-阈值距离内邻居最少的城市
  1. 解题思路
  2. 总结