1339-分裂二叉树的最大乘积

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:27 2023-09-13 16:06:27 Updated    

给你一棵二叉树，它的根为 root 。请你删除 1 条边，使二叉树分裂成两棵子树，且它们子树和的乘积尽可能大。

由于答案可能会很大，请你将结果对 10^9 + 7 取模后再返回。

示例 1：

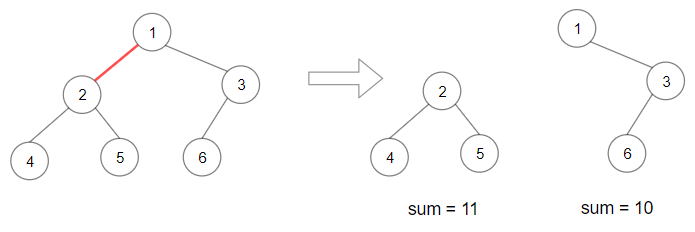
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/02/02/sample_1_1699.png)

**输入：** root = [1,2,3,4,5,6]
**输出：** 110
**解释：** 删除红色的边，得到 2 棵子树，和分别为 11 和 10 。它们的乘积是 110 （11*10）

示例 2：

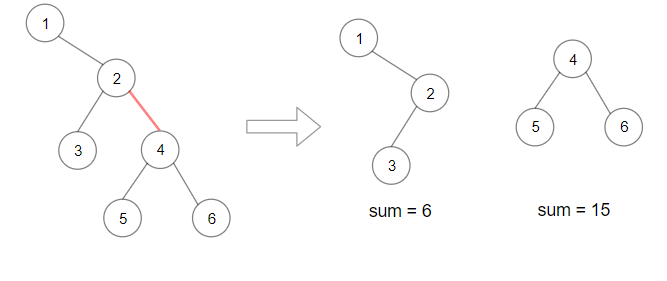
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/02/02/sample_2_1699.png)

**输入：** root = [1,null,2,3,4,null,null,5,6]
**输出：** 90
**解释：** 移除红色的边，得到 2 棵子树，和分别是 15 和 6 。它们的乘积为 90 （15*6）

示例 3：

**输入：** root = [2,3,9,10,7,8,6,5,4,11,1]
**输出：** 1025

示例 4：

**输入：** root = [1,1]
**输出：** 1

提示：

  • 每棵树最多有 50000 个节点，且至少有 2 个节点。
  • 每个节点的值在 [1, 10000] 之间。

方法一：数学

记二叉树中所有元素的值之和为 sum_r。

假设我们删除的边的两个端点为 u 和 v，其中 u 是 v 的父节点，那么在这条边删除之后，其中的一棵子树以 v 为根节点，记其中所有元素之和为 sum_v；另一棵子树以原二叉树的根节点 root 为根节点，其中元素之和为 sum_r - sum_v。我们需要找到一个节点 v，使得 (sum_v) * (sum_r - sum_v) 的值最大。

那么我们如何找到这个节点呢？我们首先使用深度优先搜索计算出 sum_r，即遍历二叉树中的每一个节点，将其对应的元素值进行累加。随后我们再次使用深度优先搜索，通过递归的方式计算出每一个节点 v 对应的子树元素之和 sum_v，并求出所有 (sum_v) * (sum_r - sum_v) 中的最大值，就可以得到答案。

由于题目中需要将结果对 10^9+7 取模，我们需要注意的是，不能在计算 (sum_v) * (sum_r - sum_v) 时将其直接对 10^9+7 取模，这是因为原先较大的数，取模之后不一定仍然较大。这一步可以有两种解决方案：

  • 我们用 64 位的整数类型（例如 long，long long 等）计算和存储 (sum_v) * (sum_r - sum_v) 的值，并在最后对 10^9+7 取模；

  • 我们使用均值不等式的知识，当 sum_r 为定值时，sum_v 越接近 sum_r 的一半，(sum_v) * (sum_r - sum_v) 的值越大。我们只需要存储最接近 sum_r 的一半的那个 sum_v，在最后计算 (sum_v) * (sum_r - sum_v) 的值并对 10^9+7 取模。

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
private:
    int sum = 0;
    int best = 0;

public:
    void dfs(TreeNode* node) {
        if (!node) {
            return;
        }
        sum += node->val;
        dfs(node->left);
        dfs(node->right);
    }

    int dfs2(TreeNode* node) {
        if (!node) {
            return 0;
        }
        int cur = dfs2(node->left) + dfs2(node->right) + node->val;
        if (abs(cur*2 - sum) < abs(best*2 - sum)) {
            best = cur;
        }
        return cur;
    }

    int maxProduct(TreeNode* root) {
        dfs(root);
        dfs2(root);
        return (long long)best * (sum - best) % 1000000007;
    }
};

复杂度分析

  • 时间复杂度：O(N)，其中 N 是二叉树的节点个数。

  • 空间复杂度：O(1)。

 Comments
On this page
1339-分裂二叉树的最大乘积