1344-时钟指针的夹角
给你两个数 hour 和 minutes 。请你返回在时钟上,由给定时间的时针和分针组成的较小角的角度(60 单位制)。
示例 1:
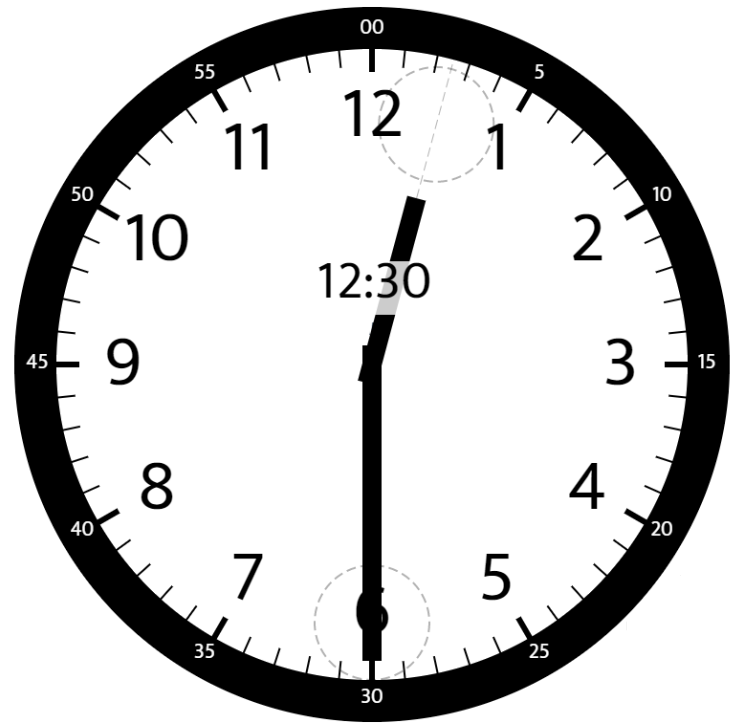
**输入:** hour = 12, minutes = 30
**输出:** 165
示例 2:
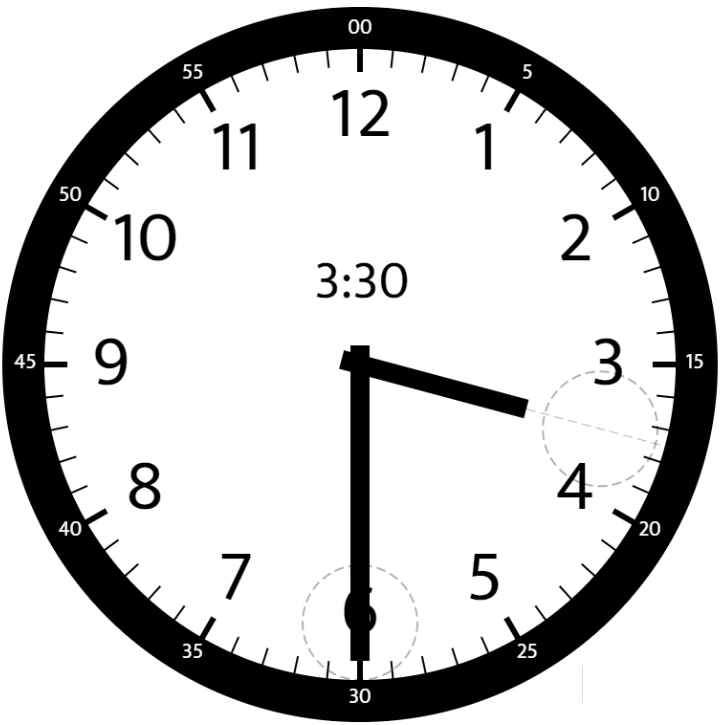
**输入:** hour = 3, minutes = 30
**输出;** 75
示例 3:
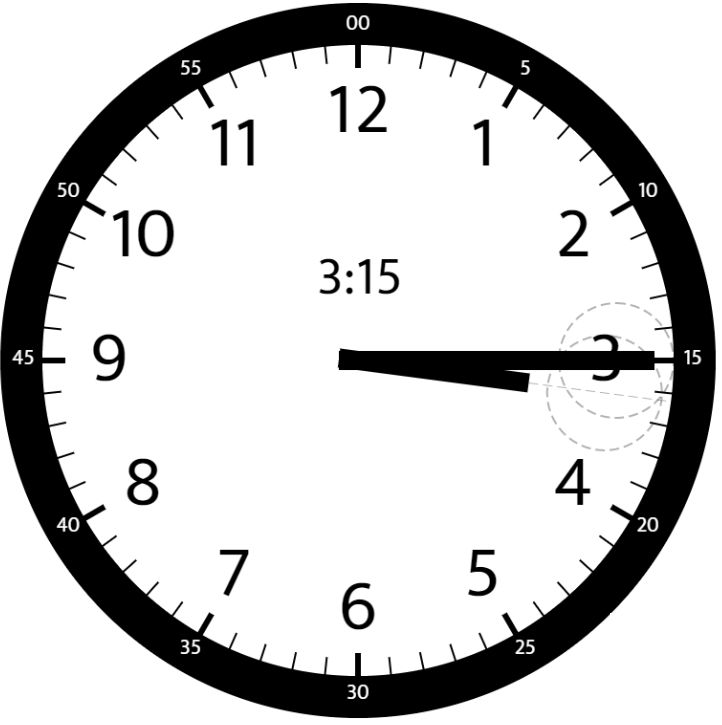
**输入:** hour = 3, minutes = 15
**输出:** 7.5
示例 4:
**输入:** hour = 4, minutes = 50
**输出:** 155
示例 5:
**输入:** hour = 12, minutes = 0
**输出:** 0
提示:
1 <= hour <= 120 <= minutes <= 59- 与标准答案误差在
10^-5以内的结果都被视为正确结果。
方法一:数学
其思想是分别计算 0 点垂线与每个指针之间的角度。答案是这两个角度的差。
 {:width=400}
{:width=400}
分针的角度:
我们从分针开始,整个圆 360° 有 60 分钟。分针指针移动一分钟的角度是 1 \text{ min} = 360° / 60 = 6°。
 {:width=400}
{:width=400}
现在可以很容易地找到 0 点垂直线和分钟指针之间的角度:minutes_angle} = \text{minutes} \times 6°。
 {:width=400}
{:width=400}
时针的角度:
与分针的角度相似,整个圆 360° 有 12 个小时,因此每个小时 1 \text{h} = 360° / 12 = 30°。
 {:width=400}
{:width=400}
则时针的角度为:hour_angle} = \text{hour} \times 30°。
 {:width=400}
{:width=400}
由于 12 点的角度实际为 0,则需要修改表达式为:hour_angle} = (\text{hour mod } 12) \ \times 30°。
在分钟指针大于 0 的情况下,必须考虑到时针指针额外的移动:它不在整数值之间跳跃,是跟着分针移动。
\text{hour_angle} = \left(\text{hour mod } 12 + \text{minutes} / 60 \right)\times 30°
 {:width=400}
{:width=400}
算法:
- 初始化常数:
one_min_angle = 6,one_hour_angle = 30。 - 分针指针与 0 点垂线的角度为:
minutes_angle = one_min_angle * minutes。 - 时针指针与 0 点垂线的角度为:
hour_angle = (hour % 12 + minutes / 60) * one_hour_angle。 - 得到差:
diff = abs(hour_angle - minutes_angle)。 - 返回最小的角度:
min(diff, 360 - diff)。
1 | class Solution: |
1 | class Solution { |
1 | class Solution { |
1 | func angleClock(hour int, minutes int) float64 { |
复杂度分析
- 时间复杂度:\mathcal{O}(1)。
- 空间复杂度:\mathcal{O}(1)。