1353-最多可以参加的会议数目
给你一个数组 events,其中 events[i] = [startDayi, endDayi] ,表示会议 i 开始于startDayi ,结束于 endDayi 。
你可以在满足 startDayi <= d <= endDayi 中的任意一天 d 参加会议 i 。注意,一天只能参加一个会议。
请你返回你可以参加的 **最大 **会议数目。
示例 1:
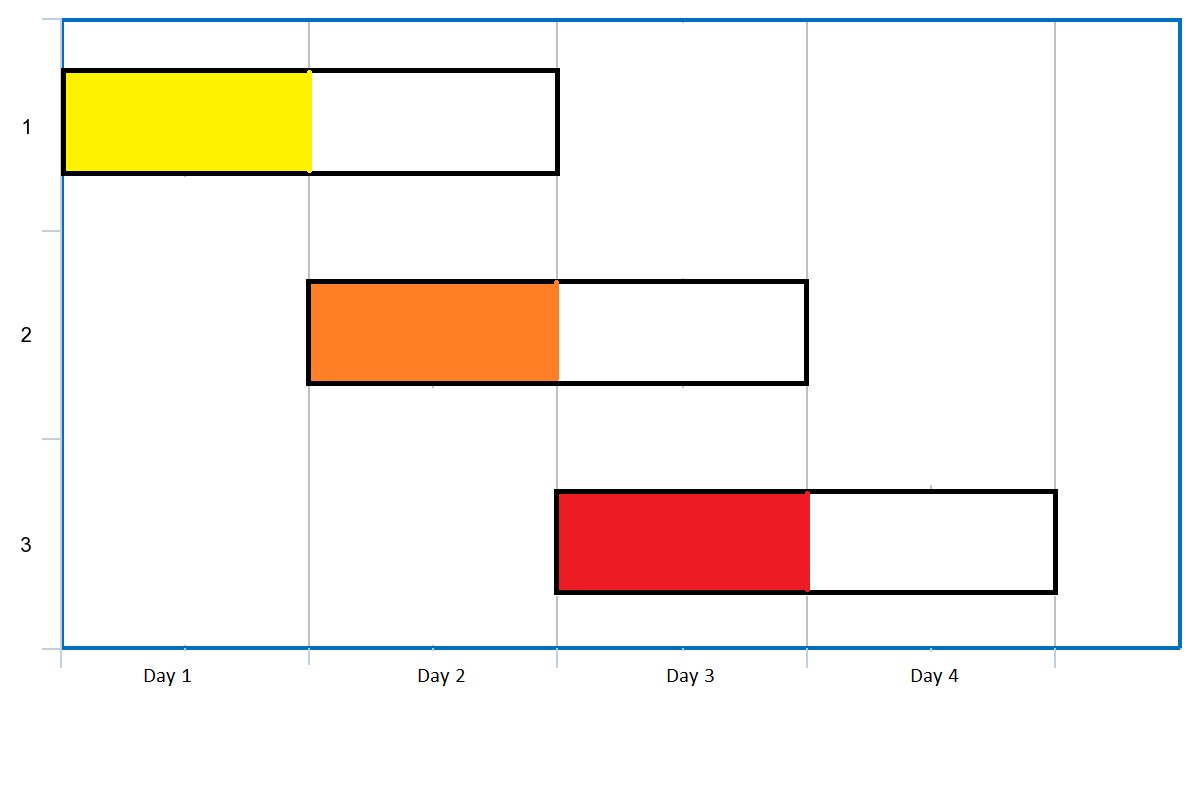
**输入:** events = [[1,2],[2,3],[3,4]]
**输出:** 3
**解释:** 你可以参加所有的三个会议。
安排会议的一种方案如上图。
第 1 天参加第一个会议。
第 2 天参加第二个会议。
第 3 天参加第三个会议。
示例 2:
**输入:** events= [[1,2],[2,3],[3,4],[1,2]]
**输出:** 4
提示:
1 <= events.length <= 105events[i].length == 21 <= startDayi <= endDayi <= 105
解题思路:
贪心的思想,对于第 i 天,如果有若干的会议都可以在这一天开,那么我们肯定是让 endDay 小的会议先在这一天开才会使答案最优,因为 endDay 大的会议可选择的空间是比 endDay 小的多的,所以在满足条件的会议需要让 endDay 小的先开。
我们开两个数组和一个 set:
- in[i]:表示在第 i 天开始的会议
- out[i]:表示在第 i 天有些会议结束了
- set<pair<int,int> >:存放当前时间下可以开的会议,用 (endDay_i,i) 这个二元组标记。
即对于第 x 个会议,我们在 in[events[x][0]] 和 out[events[x][1]+1] 处加入 x,则我们从按时间从小往大扫过去,对于第 i 天我们遍历 in[i],把第 i 天开始的会议全部加入 set,再遍历 out[i],把这一天结束的会议全部从 set 里拿出来。相当于对于会议 x,它在第 events[x][0] 天加入 set,直到第 events[x][1]+1 天才会被抹去,那么我们根据这个就可以知道第 i 天的所有可以开的会议就都在 set 里了。
最后基于我们上面分析的贪心的思想,我们直接从 set 里拿出 endDay 最小的会议,然后删除,表示在第 i 天我们开了这个会议即可,set 内部是有序的,可以直接 O(1) 取出我们要的会议,当然这里也可以用别的数据结构来替代我们的 set,比如优先队列,它们支持的都是 O(1) 取出最小值,O(logn) 插入删除,这样可以保证时间复杂度是正确的。
1 | class Solution { |
复杂度分析
- 时间复杂度:O(Slogn),S=max_{i=0}^{events.length-1}{evens[i][1],即时间点的上界,set 插入删除均要 logn 的时间。
- 空间复杂度:O(S)。