1367-二叉树中的链表

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:30 2023-09-13 16:06:30 Updated    

给你一棵以 root 为根的二叉树和一个 head 为第一个节点的链表。

如果在二叉树中，存在一条一直向下的路径，且每个点的数值恰好一一对应以 head 为首的链表中每个节点的值，那么请你返回 True ，否则返回
False 。

一直向下的路径的意思是：从树中某个节点开始，一直连续向下的路径。

示例 1：

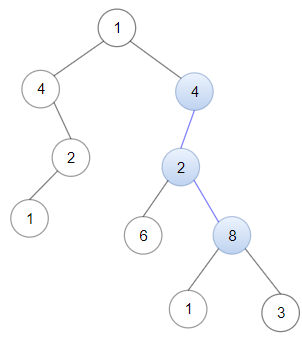
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/02/29/sample_1_1720.png)

**输入：** head = [4,2,8], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3]
**输出：** true
**解释：** 树中蓝色的节点构成了与链表对应的子路径。

示例 2：

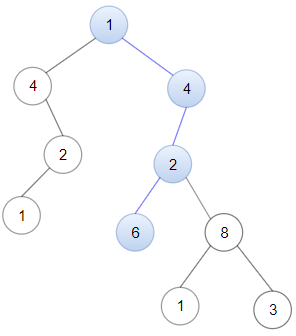
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/02/29/sample_2_1720.png)

**输入：** head = [1,4,2,6], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3]
**输出：** true

示例 3：

**输入：** head = [1,4,2,6,8], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3]
**输出：** false
**解释：** 二叉树中不存在一一对应链表的路径。

提示：

  • 二叉树和链表中的每个节点的值都满足 1 <= node.val <= 100 。
  • 链表包含的节点数目在 1 到 100 之间。
  • 二叉树包含的节点数目在 1 到 2500 之间。

方法一：枚举

枚举二叉树中的每个节点为起点往下的路径是否有与链表相匹配的路径。为了判断是否匹配我们设计一个递归函数 dfs(rt,\textit{head}) ，其中 rt 表示当前匹配到的二叉树节点，head 表示当前匹配到的链表节点，整个函数返回布尔值表示是否有一条该节点往下的路径与 head 节点开始的链表匹配，如匹配返回 true，否则返回 false ，一共有四种情况：

  1. 链表已经全部匹配完，匹配成功，返回 true

  2. 二叉树访问到了空节点，匹配失败，返回 false

  3. 当前匹配的二叉树上节点的值与链表节点的值不相等，匹配失败，返回 false

  4. 前三种情况都不满足，说明匹配成功了一部分，我们需要继续递归匹配，所以先调用函数 dfs(rt\rightarrow left,head\rightarrow next) ，其中 rt\rightarrow left 表示该节点的左儿子节点， head\rightarrow next 表示下一个链表节点，如果返回的结果是 false，说明没有找到相匹配的路径，需要继续在右子树中匹配，继续递归调用函数 dfs(rt\rightarrow right,head\rightarrow next) 去找是否有相匹配的路径，其中 rt\rightarrow right 表示该节点的右儿子节点， head\rightarrow next 表示下一个链表节点。

匹配函数确定了，剩下只要枚举即可，从根节点开始，如果当前节点匹配成功就直接返回 true ，否则继续找它的左儿子和右儿子是否满足，也就是代码中的 dfs(root,head) || isSubPath(head,root->left) || isSubPath(head,root->right) ，然后不断的递归调用。

这样枚举所有节点去判断即能找出是否有一条与链表相匹配的路径。

[]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    bool dfs(TreeNode* rt, ListNode* head) {
        // 链表已经全部匹配完，匹配成功
        if (head == NULL) return true;
        // 二叉树访问到了空节点，匹配失败
        if (rt == NULL) return false;
        // 当前匹配的二叉树上节点的值与链表节点的值不相等，匹配失败
        if (rt->val != head->val) return false;
        return dfs(rt->left, head->next) || dfs(rt->right, head->next);
    }
public:
    bool isSubPath(ListNode* head, TreeNode* root) {
        if (root == NULL) return false;
        return dfs(root, head) || isSubPath(head, root->left) || isSubPath(head, root->right);
    }
};
[]
1
2
3
4
5
6
7
8
9
10
var dfs = function(rt, head) {
    if (head == null) return true;
    if (rt == null) return false;
    if (rt.val != head.val) return false;
    return dfs(rt.left, head.next) || dfs(rt.right, head.next);
}
var isSubPath = function(head, root) {
    if (root == null) return 0;
    return dfs(root, head) || isSubPath(head, root.left) || isSubPath(head, root.right);
};
[]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def dfs(self, head: ListNode, rt: TreeNode) -> bool:
        if not head:
            return True
        if not rt:
            return False
        if rt.val != head.val:
            return False
        return self.dfs(head.next, rt.left) or self.dfs(head.next, rt.right)

    def isSubPath(self, head: ListNode, root: TreeNode) -> bool:
        if not root:
            return False
        return self.dfs(head, root) or self.isSubPath(head, root.left) or self.isSubPath(head, root.right)

复杂度分析

  • 时间复杂度：最坏情况下需要对所有节点进行匹配。假设一共有 n 个节点，对于一个节点为根的子树，如果它是满二叉树，且每次匹配均为到链表的最后一个节点的时候匹配失败，那么一共被匹配到的节点数为 2^{len+1}-1 ，即这个节点为根的子树往下 len 层的满二叉树的节点数，其中 len 为链表的长度，而二叉树总节点数最多 n 个，所以枚举节点最多匹配 min(2^{len+1},n) 次，最坏情况下需要 O(n* min(2^{len+1},n)) 的时间复杂度。

  • 空间复杂度：由于递归函数在递归过程中需要为每一层递归函数分配栈空间，所以这里需要额外的空间且该空间取决于递归的深度。考虑枚举一个节点为起点递归判断所需的空间，假设该节点在第 x 层，即递归枚举时已经用了 O(x) 的空间，这个节点再往下匹配链表长度 y 层节点时需要使用 O(y) 的空间，所以一共需要 O(x+y) 的空间，而 x+y 必然不会超过树的高度，所以最后的空间复杂度为树的高度，即 O(height) ，height 为树的高度。

 Comments
On this page
1367-二叉树中的链表