1368-使网格图至少有一条有效路径的最小代价

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 17:01:07 2023-09-13 17:01:07 Updated    

给你一个 m x n 的网格图 grid 。 grid 中每个格子都有一个数字，对应着从该格子出发下一步走的方向。 grid[i][j]
中的数字可能为以下几种情况：

  • 1 ，下一步往右走，也就是你会从 grid[i][j] 走到 grid[i][j + 1]
  • 2 ，下一步往左走，也就是你会从 grid[i][j] 走到 grid[i][j - 1]
  • 3 ，下一步往下走，也就是你会从 grid[i][j] 走到 grid[i + 1][j]
  • 4 ，下一步往上走，也就是你会从 grid[i][j] 走到 grid[i - 1][j]

注意网格图中可能会有 无效数字 ，因为它们可能指向 grid 以外的区域。

一开始，你会从最左上角的格子 (0,0) 出发。我们定义一条 有效路径 为从格子 (0,0)
出发，每一步都顺着数字对应方向走，最终在最右下角的格子 (m - 1, n - 1) 结束的路径。有效路径 不需要是最短路径 。

你可以花费 cost = 1 的代价修改一个格子中的数字，但每个格子中的数字 只能修改一次 。

请你返回让网格图至少有一条有效路径的最小代价。

示例 1：

![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/02/29/grid1.png)

**输入：** grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]]
**输出：** 3
**解释：** 你将从点 (0, 0) 出发。
到达 (3, 3) 的路径为： (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) 花费代价 cost = 1 使方向向下 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) 花费代价 cost = 1 使方向向下 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) 花费代价 cost = 1 使方向向下 --> (3, 3)
总花费为 cost = 3.

示例 2：

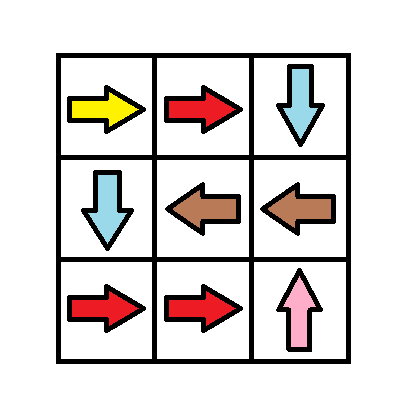
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/02/29/grid2.png)

**输入：** grid = [[1,1,3],[3,2,2],[1,1,4]]
**输出：** 0
**解释：** 不修改任何数字你就可以从 (0, 0) 到达 (2, 2) 。

示例 3：

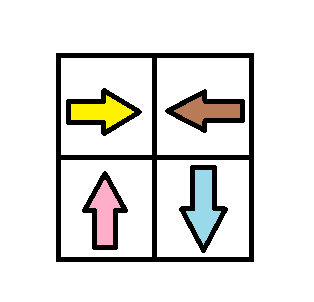
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/02/29/grid3.png)

**输入：** grid = [[1,2],[4,3]]
**输出：** 1

示例 4：

**输入：** grid = [[2,2,2],[2,2,2]]
**输出：** 3

示例 5：

**输入：** grid = [[4]]
**输出：** 0

提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 100

分析

如果没有「每个格子中的数字只能修改一次」这个条件，我们可以很轻松地将本题建模成一个求最短路径的问题：

  • 我们希望求出从左上角 (0, 0) 到右下角 (m - 1, n - 1) 的「最小代价」；

  • 当我们在任意位置 (i, j) 时，我们都可以向上、下、左、右移动一个位置，但不能走出边界。如果移动的位置与 (i, j) 处的箭头方向一致，那么移动的代价为 0，否则为 1；

  • 这样以来，我们可以将数组 grid 建模成一个包含 mn 个节点和不超过 4mn 条边的有向图 G。图 G 中的每一个节点表示数组 grid 中的一个位置，它会向不超过 4 个相邻的节点各连出一条边，边的权值要么为 0（移动方向与箭头方向一致），要么为 1（移动方向与箭头方向不一致）；

  • 我们在图 G 上使用任意一种最短路算法，求出从 (0, 0) 到 (m - 1, n - 1) 的最短路，即可得到答案。

那么在加上了这个条件之后，这样的建模方式还是可行的吗？我们可以发现，一定存在一条最短路径，它只经过每个位置最多一次，这是因为如果一条最短路径能表示成如下的形式：

P_0, P_1, \cdots, P_k, P_{k_{11} }, \cdots, P_{k_{1x} }, P_k, P_{k_{21} }, \cdots, P_{k_{2y} }

其中 P_i 表示某个位置。该路径经过了位置 P_k 两次，那么我们可以删去这两次 P_k 之间的所有位置以及任意一次 P_k，得到一条新的最短路径：

P_0, P_1, \cdots, P_k, P_{k_{21} }, \cdots, P_{k_{2y} }

这条最短路径只经过了位置 P_k 一次。用同样的方法，我们可以继续删去最短路径中出现超过一次的位置，最终得到一条只经过每个位置最多一次的最短路径。对于这条路径，无论有没有「每个格子中的数字只能修改一次」这个条件，它都不会受到影响，因此我们仍然可以使用上述的建模方式，求出最短路并作为最终答案。

方法一：Dijkstra 算法

Dijkstra 算法适合用来求出无负权边图中的单源最短路径。其中「无负权边」表示图中所有边的权值必须为非负数，「单源最短路径」表示 Dijkstra 算法可以求出从某一个节点到其余所有节点的最短路径。由于我们的建模中，所有边的权值均为 0 或 1，并且我们只需要求出从 (0, 0) 到 (m - 1, n - 1) 的最短路，因此我们可以直接套用 Dijkstra 算法得到答案。

Dijkstra 算法本身的实现不是这篇题解的重点，如果读者不了解该算法，可以使用搜索引擎自行学习。下面的代码实现的是使用优先队列优化的 Dijsktra 算法。

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
using PII = pair<int, int>;

class Solution {
private:
    static constexpr int dirs[4][2] = { {0, 1}, {0, -1}, {1, 0}, {-1, 0} };

public:
    int minCost(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        vector<int> dist(m * n, INT_MAX);
        vector<int> seen(m * n, 0);
        dist[0] = 0;
        priority_queue<PII, vector<PII>, greater<PII>> q;
        q.emplace(0, 0);
        
        while (!q.empty()) {
            auto [cur_dis, cur_pos] = q.top();
            q.pop();
            if (seen[cur_pos]) {
                continue;
            }
            seen[cur_pos] = 1;
            int x = cur_pos / n;
            int y = cur_pos % n;
            for (int i = 0; i < 4; ++i) {
                int nx = x + dirs[i][0];
                int ny = y + dirs[i][1];
                int new_pos = nx * n + ny;
                int new_dis = cur_dis + (grid[x][y] != i + 1);
                
                if (nx >= 0 && nx < m && ny >= 0 && ny < n && new_dis < dist[new_pos]) {
                    dist[new_pos] = new_dis;
                    q.emplace(new_dis, new_pos);
                }
            }
        }

        return dist[m * n - 1];
    }
};
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution:
    def minCost(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        BIG = int(1e9)
        dist = [0] + [BIG] * (m * n - 1)
        seen = set()
        q = [(0, 0, 0)]

        while len(q) > 0:
            cur_dis, x, y = heapq.heappop(q)
            if (x, y) in seen:
                continue
            seen.add((x, y))
            cur_pos = x * n + y
            for i, (nx, ny) in enumerate([(x, y + 1), (x, y - 1), (x + 1, y), (x - 1, y)]):
                new_pos = nx * n + ny
                new_dis = dist[cur_pos] + (1 if grid[x][y] != i + 1 else 0)
                if 0 <= nx < m and 0 <= ny < n and new_dis < dist[new_pos]:
                    dist[new_pos] = new_dis
                    heapq.heappush(q, (new_dis, nx, ny))
        
        return dist[m * n - 1]

复杂度分析

  • 时间复杂度：O(MN \log (MN))。优先队列优化的 Dijsktra 算法的时间复杂度为 O((M + N)\log M)，其中 N 和 M 分别是图中的点数和边数。在我们的建模中，点的数量为 MN，边的数量不超过 4MN 但与 4MN 同阶，带入即可得到时间复杂度为 O(MN \log (MN))。

  • 空间复杂度：O(MN)。优先队列优化的 Dijkstra 算法需要用到最多 M 个元素的优先队列（堆）以及若干长度为 N 表示状态的数组。带入我们建模中的点数和边数，即可得到空间复杂度为 O(MN)。

说明

除了 Dijkstra 算法以外，常用的最短路算法还有：

  • Floyd 算法：在 O(N^3) 的时间内计算图中任意两个节点之间的最短路，对图中的边权没有要求；

  • Bellman-Ford 算法：在 O(MN) 的时间内计算单源最短路，对图中的边权没有要求。

其中 N 和 M 分别是图中的点数和边数。此外还有一种 SPFA 算法，它在 Bellman-Ford 算法的基础上使用队列优化，使得在随机图上可以达到平均 O(M) 的时间复杂度（论文中只有测试结果，无证明）。但需要指出的是，在最坏情况下，SPFA 算法的时间复杂度仍为 O(MN)。如果图中的边权均为非负整数，那么 Dijkstra 算法在最坏情况下的时间复杂度 O((M + N) \log M) 是远远优于 SPFA 算法的。因此我们不能错误地认为 SPFA 算法是一种在任何情况下都高效的算法。如果可以使用 Dijkstra 算法，就尽量不要使用 SPFA 算法。

方法二：0-1 广度优先搜索

常规的广度优先搜索可以找出在边权均为 1 时的单源最短路，然而在我们的建模中，边权除了 1 之外也可能为 0。我们是否可以修改广度优先搜索的算法框架，使得它可以找出在边权为 0 或 1 时的单源最短路呢？

答案是可以的。这种修改过的广度优先搜索被称为「0-1 广度优先搜索」，这里 有一篇很详细的教程。

保证广度优先搜索正确性的基础在于：对于源点 s 以及任意两个节点 u 和 v，如果 dist}(s, u) < \textit{dist}(s, v)（其中 dist}(x, y) 表示从节点 x 到节点 y 的最短路长度），那么节点 u 一定会比节点 v 先被取出队列。在常规的广度优先搜索中，我们使用队列作为维护节点的数据结构，就保证了从队列中取出的节点，它们与源点之间的距离是单调递增的。然而如果边权可能为 0，就会出现如下的情况：

  • 源点 s 被取出队列；

  • 源点 s 到节点 v_1 有一条权值为 1 的边，将节点 v_1 加入队列；

  • 源点 s 到节点 v_2 有一条权值为 0 的边，将节点 v_2 加入队列；

此时节点 v_2 一定会在节点 v_1 之后被取出队列，但节点 v_2 与源点之间的距离反而较小，这样就破坏了广度优先搜索正确性的基础。

那么我们如何修改广度优先搜索的算法框架呢？我们可以使用双端队列（double-ended queue, deque）代替普通的队列作为维护节点的数据结构。当任一节点 u 被取出队列时，如果它到某节点 v_i 有一条权值为 0 的边，那么就将节点 v_i 加入双端队列的「队首」。如果它到某节点 v_j 有一条权值为 1 的边，那么和常规的广度优先搜索相同，我们将节点 v_j 加入双端队列的「队尾」。这样以来，我们保证了任意时刻从队首到队尾的所有节点，它们与源点之间的距离是单调递增的，即从队列中取出的节点与源点之间的距离同样是单调递增的。

0-1 广度优先搜索的实现其实与 Dijkstra 算法非常相似。在 Dijkstra 算法中，我们用优先队列保证了距离的单调递增性。而在 0-1 广度优先搜索中，实际上任意时刻队列中的节点与源点的距离均为 d 或 d + 1（其中 d 为某一非负整数），并且所有与源点距离为 d 的节点都出现在队首附近，所有与源点距离为 d + 1 的节点都出现在队尾附近。因此，我们只要使用双端队列，对于边权为 0 和 1 的两种情况分别将对应节点添加至队首和队尾，就保证了距离的单调递增性。

[sol2-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
using PII = pair<int, int>;

class Solution {
private:
    static constexpr int dirs[4][2] = { {0, 1}, {0, -1}, {1, 0}, {-1, 0} };

public:
    int minCost(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        vector<int> dist(m * n, INT_MAX);
        vector<int> seen(m * n, 0);
        dist[0] = 0;
        deque<int> q;
        q.push_back(0);
        
        while (!q.empty()) {
            auto cur_pos = q.front();
            q.pop_front();
            if (seen[cur_pos]) {
                continue;
            }
            seen[cur_pos] = 1;
            int x = cur_pos / n;
            int y = cur_pos % n;
            for (int i = 0; i < 4; ++i) {
                int nx = x + dirs[i][0];
                int ny = y + dirs[i][1];
                int new_pos = nx * n + ny;
                int new_dis = dist[cur_pos] + (grid[x][y] != i + 1);
                
                if (nx >= 0 && nx < m && ny >= 0 && ny < n && new_dis < dist[new_pos]) {
                    dist[new_pos] = new_dis;
                    if (grid[x][y] == i + 1) {
                        q.push_front(new_pos);
                    }
                    else {
                        q.push_back(new_pos);
                    }
                }
            }
        }

        return dist[m * n - 1];
    }
};
[sol2-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution:
    def minCost(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        BIG = int(1e9)
        dist = [0] + [BIG] * (m * n - 1)
        seen = set()
        q = collections.deque([(0, 0)])

        while len(q) > 0:
            x, y = q.popleft()
            if (x, y) in seen:
                continue
            seen.add((x, y))
            cur_pos = x * n + y
            for i, (nx, ny) in enumerate([(x, y + 1), (x, y - 1), (x + 1, y), (x - 1, y)]):
                new_pos = nx * n + ny
                new_dis = dist[cur_pos] + (1 if grid[x][y] != i + 1 else 0)
                if 0 <= nx < m and 0 <= ny < n and new_dis < dist[new_pos]:
                    dist[new_pos] = new_dis
                    if grid[x][y] == i + 1:
                        q.appendleft((nx, ny))
                    else:
                        q.append((nx, ny))
        
        return dist[m * n - 1]

复杂度分析

  • 时间复杂度：O(MN)。在常规的广度优先搜索中，每个节点最多被添加进队列一次，而在 0-1 广度优先搜索中，每个节点最多被添加进双端队列两次（即队首一次，队尾一次）。

  • 空间复杂度：O(MN)，与常规的广度优先搜索一致。

 Comments
On this page
1368-使网格图至少有一条有效路径的最小代价