1382-将二叉搜索树变平衡
给你一棵二叉搜索树,请你返回一棵 平衡后 的二叉搜索树,新生成的树应该与原来的树有着相同的节点值。如果有多种构造方法,请你返回任意一种。
如果一棵二叉搜索树中,每个节点的两棵子树高度差不超过 1 ,我们就称这棵二叉搜索树是 平衡的 。
示例 1:
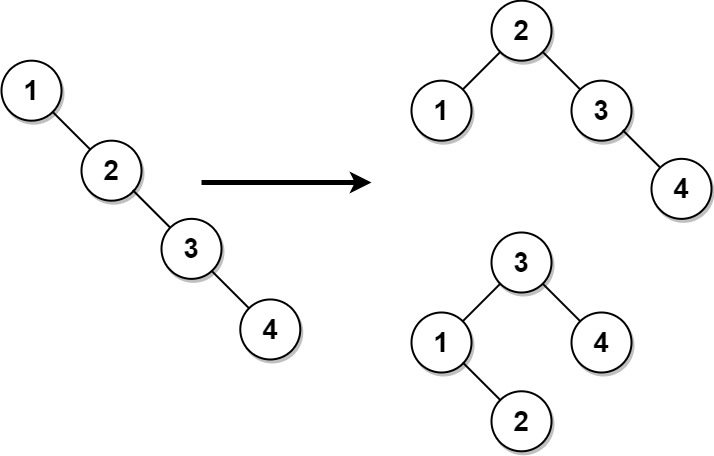
**输入:** root = [1,null,2,null,3,null,4,null,null]
**输出:** [2,1,3,null,null,null,4]
**解释:** 这不是唯一的正确答案,[3,1,4,null,2,null,null] 也是一个可行的构造方案。
示例 2:
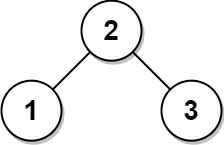
**输入:** root = [2,1,3]
**输出:** [2,1,3]
提示:
- 树节点的数目在
[1, 104]范围内。 1 <= Node.val <= 105
方法一:贪心构造
思路
「平衡」要求它是一棵空树或它的左右两个子树的高度差的绝对值不超过 1,这很容易让我们产生这样的想法——左右子树的大小越「平均」,这棵树会不会越平衡?于是一种贪心策略的雏形就形成了:我们可以通过中序遍历将原来的二叉搜索树转化为一个有序序列,然后对这个有序序列递归建树,对于区间 [L, R]:
取 {\rm mid} = \lfloor L + R}{2} \rfloor ,即中心位置作为当前节点的值;
如果 L \leq {\rm mid} - 1,那么递归地将区间 [L, {\rm mid} - 1] 作为当前节点的左子树;
如果 {\rm mid} + 1 \leq R,那么递归地将区间 [{\rm mid} + 1, R] 作为当前节点的右子树。
思考:如何证明这个贪心是正确的呢?
要证明我们构造的这颗树是平衡的,就要证明这棵树根结点为空或者左右两个子树的高度差的绝对值不超过 1。
观察这个过程,我们不难发现它和二分查找非常相似。对于一个长度为 x 的区间,由它构建出的二叉树的最大高度应该等于对长度为 x 的有序序列进行二分查找「查找成功」时的「最大」比较次数,为 \lfloor \log_2 x \rfloor + 1,记为 h(x)。
「引理 A」 长度为 k 的区间与长度为 k + 1 的区间(其中 k \geq 1)按照以上方法构造出的二叉树的最大高度差不超过 1。证明过程如下:
要证明「引理 A」即我们要证明:
\begin{aligned}
h(k + 1) - h(k)
= & [\lfloor \log_2 (k + 1) \rfloor + 1] - [\lfloor \log_2 (k) \rfloor + 1] \\
= & \lfloor \log_2 (k + 1) \rfloor - \lfloor \log_2 (k) \rfloor \leq 1
\end{aligned}
由此我们可以证明不等式:
\lfloor \log_2 (k + 1) \rfloor \leq \lfloor \log_2 (k) \rfloor + 1
设 k = 2^r + b,其中 0 \leq b < 2^r,那么 k \in [2^{r}, 2^{r+1}),\lfloor \log k \rfloor = r,不等式右边等于 r + 1。因为 k \in [2^{r}, 2^{r+1}),所以 k + 1 \in (2^{r}, 2^{r+1}],故 \lceil \log_2 (k + 1) \rceil = r + 1,即右边等于 \lceil \log_2 (k + 1) \rceil。所以我们需要证明:
\lfloor \log_2 (k + 1) \rfloor \leq \lceil \log_2 (k + 1) \rceil
显然成立,由此逆推可得,「引理 A」成立。
下面我们来证明这个贪心算法的正确性:即按照这个方法构造出的二叉树左右子树都是平衡的,并且左右子树的高度差不超过 1。
「正确性证明」 假设我们要讨论的区间长度为 k,我们用数学归纳法来证明:
k = 1,k = 2 时显然成立;
假设 k = m 和 k = m + 1 时正确性成立。
那么根据「引理 A」,长度为 m 和 m + 1 的区间构造出的子树都是平衡的,并且它们的高度差不超过 1;
当 k = 2(m + 1) - 1 时,创建出的节点的值等于第 m + 1 个元素的值,它的左边和右边各有长度为 m 的区间,根据「假设推论」,k = 2(m + 1) - 1 时构造出的左右子树都是平衡树,且树形完全相同,故高度差为 0,所以 k = 2(m + 1) - 1 时,正确性成立;
当 k = 2(m + 1) 时,创建出的节点的值等于第 m + 1 个元素的值,它的左边的区间长度为 m,右边区间的长度为 m + 1,那么 k = 2(m + 1) 时构造出的左右子树都是平衡树,且高度差不超过 1,所以 k = 2(m + 1) 时,正确性成立;
通过这种归纳方法,可以覆盖所有的 k \geq 1。故在 k \geq 1 时,正确性成立,证毕。
1 | class Solution { |
1 | class Solution { |
1 | class Solution: |
复杂度分析
假设节点总数为 n。
时间复杂度:获得中序遍历的时间代价是 O(n);建立平衡二叉树的时建立每个点的时间代价为 O(1),总时间也是 O(n)。故渐进时间复杂度为 O(n)。
空间复杂度:这里使用了一个数组作为辅助空间,存放中序遍历后的有序序列,故渐进空间复杂度为 O(n)。