1386-安排电影院座位

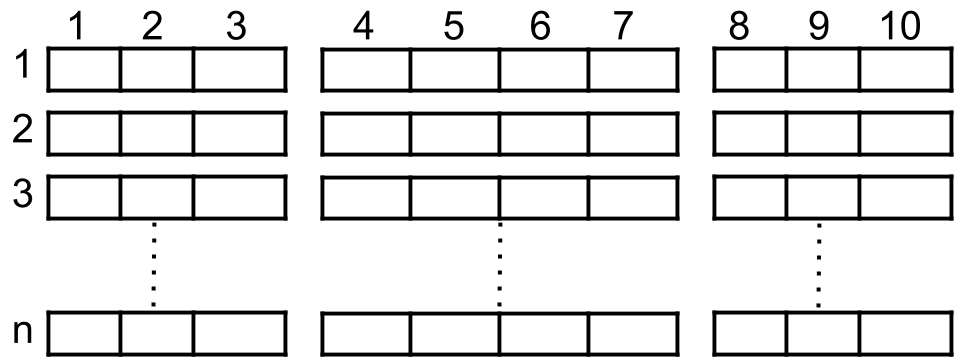
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/03/21/cinema_seats_1.png)

如上图所示，电影院的观影厅中有 n 行座位，行编号从 1 到 n ，且每一行内总共有 10 个座位，列编号从 1 到 10 。

给你数组 reservedSeats ，包含所有已经被预约了的座位。比如说，researvedSeats[i]=[3,8] ，它表示第 3
行第 8 个座位被预约了。

请你返回 最多能安排多少个 4 人家庭 。4 人家庭要占据 **同一行内连续 **的 4 个座位。隔着过道的座位（比方说 [3,3] 和
[3,4]）不是连续的座位，但是如果你可以将 4 人家庭拆成过道两边各坐 2 人，这样子是允许的。

示例 1：

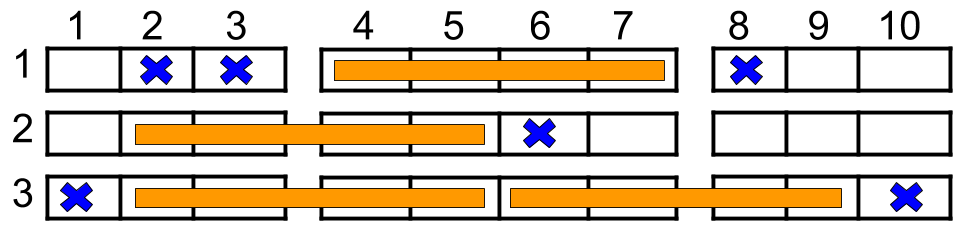
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/03/21/cinema_seats_3.png)

**输入：** n = 3, reservedSeats = [[1,2],[1,3],[1,8],[2,6],[3,1],[3,10]]
**输出：** 4
**解释：** 上图所示是最优的安排方案，总共可以安排 4 个家庭。蓝色的叉表示被预约的座位，橙色的连续座位表示一个 4 人家庭。

示例 2：

**输入：** n = 2, reservedSeats = [[2,1],[1,8],[2,6]]
**输出：** 2

示例 3：

**输入：** n = 4, reservedSeats = [[4,3],[1,4],[4,6],[1,7]]
**输出：** 4

提示：

1 <= n <= 10^9
1 <= reservedSeats.length <= min(10*n, 10^4)
reservedSeats[i].length == 2
1 <= reservedSeats[i][0] <= n
1 <= reservedSeats[i][1] <= 10
所有 reservedSeats[i] 都是互不相同的。

方法一：位运算

对于一个家庭而言，只有以下三种给他们安排座位的方法：

安排位置 2，3，4，5；
安排位置 4，5，6，7；
安排位置 6，7，8，9。

因此每一排的位置 1 和位置 10 都是没有意义的，即使被预约了也对答案没有任何影响。从下面的叙述开始，我们忽略所有在位置 1 和位置 10 的预约。同时我们可以发现，如果一排位置没有被预约，那么恰好可以安排给两个家庭，即给一个家庭安排位置 2，3，4，5，给另一个家庭安排位置 6，7，8，9；如果一排位置被预约了至少一个座位，那么最多只能安排给一个家庭了。

这样以来，我们可以使用 8 个二进制位表示一排座位的预约情况，这里的 8 即表示位置 2 到位置 9 的这些座位。如果位置 i 的座位被预约，那么第 i-2 个二进制位为 1，否则为 0。例如在示例一中，每一排对应的二进制数分别为：

第一排：预约了位置 2，3，8，那么二进制数为 (01000011)_2；
第二排：预约了位置 6，那么二进制数为 (00010000)_2；
第三排：预约了位置 1 和 10，那么二进制数为 (00000000)_2。

我们可以用哈希映射（HashMap）来存储每一排以及它们的二进制数。对于哈希映射中的每个键值对，键表示电影院中的一排，值表示这一排对应的二进制数。如果某一排没有任何位置被预约（例如上面的第三排），我们实际上知道了这一排一定可以安排给两个家庭，因此可以不必将这个键值对存放在哈希映射中。也就是说，只有某一排的某一座位被预约了，我们才将这一排放入哈希映射。

在处理完了所有的预约之后，我们遍历哈希映射。对于一个键值对 (\textit{row}, \textit{bitmask})，我们如何知道 row 这一排可以安排给几个家庭呢？根据之前的分析，被存储在哈希映射中的这些排最多只能安排给一个家庭，那么对于三种安排座位的方法：

对于安排位置 2，3，4，5，如果 bitmask 中第 0，1，2，3 个二进制位均为 0，那么就可以安排给一个家庭；也就是说，bitmask 和 (11110000)_2 的按位或值保持为 (11110000)_2 不变；
对于安排位置 4，5，6，7，如果 bitmask 中第 2，3，4，5 个二进制位均为 0，那么就可以安排给一个家庭；也就是说，bitmask 和 (11000011)_2 的按位或值保持为 (11000011)_2 不变；
对于安排位置 6，7，8，9，如果 bitmask 中第 4，5，6，7 个二进制位均为 0，那么就可以安排给一个家庭；也就是说，bitmask 和 (00001111)_2 的按位或值保持为 (00001111)_2 不变。

这样以来，我们只需要将 bitmask 分别与 (11110000)_2，(11000011)_2 和 (00001111)_2 进行按位或运算，如果其中有一个在运算后保持不变，那么 row 这一列就可以安排给一个家庭。

在最后，我们知道还有 n - |S| 列是没有任何一个位置被预约的，其中 |S| 是哈希映射中键值对的个数。这些列可以安排给两个家庭，因此最后的答案还需要加上 2(n - |S|)。

[sol1-C++]class Solution {
public:
    int maxNumberOfFamilies(int n, vector<vector<int>>& reservedSeats) {
        int left = 0b11110000;
        int middle = 0b11000011;
        int right = 0b00001111;

        unordered_map<int, int> occupied;
        for (const vector<int>& seat: reservedSeats) {
            if (seat[1] >= 2 && seat[1] <= 9) {
                occupied[seat[0]] |= (1 << (seat[1] - 2));
            }
        }

        int ans = (n - occupied.size()) * 2;
        for (auto& [row, bitmask]: occupied) {
            if (((bitmask | left) == left) || ((bitmask | middle) == middle) || ((bitmask | right) == right)) {
                ++ans;
            }
        }
        return ans;
    }
};

[sol1-Python3]class Solution:
    def maxNumberOfFamilies(self, n: int, reservedSeats: List[List[int]]) -> int:
        left, middle, right = 0b11110000, 0b11000011, 0b00001111
        occupied = collections.defaultdict(int)
        for seat in reservedSeats:
            if 2 <= seat[1] <= 9:
                occupied[seat[0]] |= (1 << (seat[1] - 2))
        
        ans = (n - len(occupied)) * 2
        for row, bitmask in occupied.items():
            if (bitmask | left) == left or (bitmask | middle) == middle or (bitmask | right) == right:
                ans += 1
        return ans

[sol1-Java]class Solution {
    public int maxNumberOfFamilies(int n, int[][] reservedSeats) {
        int left = 0b11110000;
        int middle = 0b11000011;
        int right = 0b00001111;

        Map <Integer, Integer> occupied = new HashMap <Integer, Integer> ();
        for (int[] seat: reservedSeats) {
            if (seat[1] >= 2 && seat[1] <= 9) {
                int origin = occupied.containsKey(seat[0]) ? occupied.get(seat[0]) : 0;
                int value = origin | (1 << (seat[1] - 2));
                occupied.put(seat[0], value);
            }
        }

        int ans = (n - occupied.size()) * 2;
        for (Map.Entry <Integer, Integer> entry : occupied.entrySet()) {
            int row = entry.getKey(), bitmask = entry.getValue();
            if (((bitmask | left) == left) || ((bitmask | middle) == middle) || ((bitmask | right) == right)) {
                ++ans;
            }
        }
        return ans;
    }
}

复杂度分析

时间复杂度：O(r)，其中 r 是数组 reservedSeats 的长度。我们首先对数组 reservedSeats 进行遍历并在哈希映射中记录这些预约信息，随后遍历哈希映射统计答案，这两次遍历的时间复杂度均为 O(r)。
空间复杂度：O(r)。额外的使用空间为哈希映射占用的空间，其中的键值对最多有 r 个。