1391-检查网格中是否存在有效路径

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 17:01:06 2023-09-13 17:01:06 Updated    

给你一个 m x n 的网格 grid。网格里的每个单元都代表一条街道。grid[i][j] 的街道可以是：

  • 1 表示连接左单元格和右单元格的街道。
  • 2 表示连接上单元格和下单元格的街道。
  • 3 表示连接左单元格和下单元格的街道。
  • 4 表示连接右单元格和下单元格的街道。
  • 5 表示连接左单元格和上单元格的街道。
  • 6 表示连接右单元格和上单元格的街道。

![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/03/21/main.png)

你最开始从左上角的单元格 (0,0) 开始出发，网格中的「有效路径」是指从左上方的单元格 (0,0) 开始、一直到右下方的 (m-1,n-1)
结束的路径。 该路径必须只沿着街道走 。

注意： 你 不能 变更街道。

如果网格中存在有效的路径，则返回 true，否则返回 false 。

示例 1：

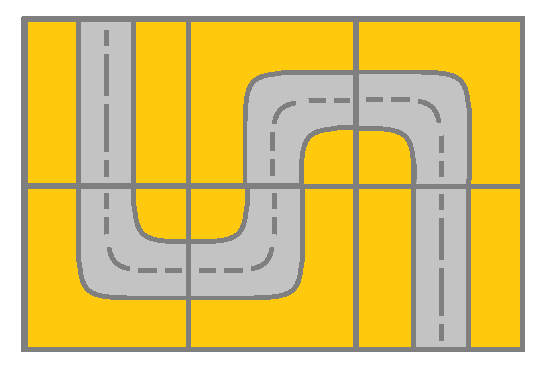
**输入：** grid = [[2,4,3],[6,5,2]]
**输出：** true
**解释：** 如图所示，你可以从 (0, 0) 开始，访问网格中的所有单元格并到达 (m - 1, n - 1) 。

示例 2：

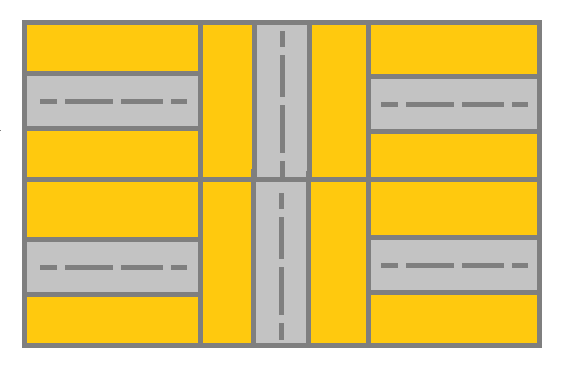
**输入：** grid = [[1,2,1],[1,2,1]]
**输出：** false
**解释：** 如图所示，单元格 (0, 0) 上的街道没有与任何其他单元格上的街道相连，你只会停在 (0, 0) 处。

示例 3：

**输入：** grid = [[1,1,2]]
**输出：** false
**解释：** 你会停在 (0, 1)，而且无法到达 (0, 2) 。

示例 4：

**输入：** grid = [[1,1,1,1,1,1,3]]
**输出：** true

示例 5：

**输入：** grid = [[2],[2],[2],[2],[2],[2],[6]]
**输出：** true

提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 300
  • 1 <= grid[i][j] <= 6

说明

静态连通性

如果题目中先给定了整个图（例如本题通过二维数组 grid 直接给出了整个网格的信息），再给出关于连通性的询问（例如本题询问起点到终点是否存在一条路径），那么称其为「静态连通性」。其相反的定义为「动态连通性」，即图的信息和关于连通性的询问是交替给出的。换句话说，在给出一次关于连通性的询问后，还可以修改图的一部分，这样就是「动态连通性」。例如，如果本题有若干次询问，每次询问给定 grid 中的一个位置，将其修改后再判断起点和终点是否存在一条路径，且询问中对 grid 的修改会保留至后续的所有询问中，这样就是一道「动态连通性」的题目。

关于本题

对于静态连通性的题目，一般来说可以使用深度优先搜索、广度优先搜索以及并查集来实现。这三种方法的相似度很高，难点都在于如何建图，即确定哪些点对之间存在一条边。在建图完成之后，我们用任意一种算法都可以很方便得判断出某两个点是否连通。

在本题解中，我们只介绍并查集的方法。我们可以把每个「单元格」看作是图上的「点」，把单元格与单元格之间的「直接可达关系」看作是「边」。这里的「直接可达关系」是指从某个单元格可以「直接」到达它上下左右某个单元格的关系：例如，单元格中的 1 表示连接左单元格和右单元格的街道，单元格中的 3 表示连接左单元格和下单元格的街道，那么当有一个 1 在 3 的左边的时候，这两个单元格就具有这种「直接可达关系」。类似的，我们也可以用并查集来维护这种关系。

那么新的问题又来了，并查集中的点是一维的，而我们这里的单元格坐标是二维的，所以我们要做的第一步是把每一个单元格坐标映射成一个唯一的整数值，作为每个单元格的 ID。假设这里的单元格一共有 m 行 n 列，左上角为 (0, 0)，右下角为 (m - 1, n - 1)，坐标 (x, y) 可以这样映射到一个唯一的整数 {\rm id：{\rm id} = x \times n + y。这样问题就得到了解决。

考虑完这些问题之后，我们发现本题的难点在于：如何快速地判断两个相邻的单元格是否直接可达呢？判断部分的代码编写复杂度直接影响了代码编写的难易程度和可读性，因此下面我们介绍两种不同的判断方法。

方法一：相邻关系建图

思路

一种简单的判断方法是：对于数组 grid 中的某个单元格 (x, y)，根据 grid[x][y] 值的不同，它最多会连接两个不同方向的单元格。我们实现四个函数 detectL(x, y)、detectR(x, y)、detectU(x, y) 以及 detectD(x, y)，在 (x, y) 连接了左、右、上、下四个方向时分别调用对应的函数。例如当 grid[x][y] 的值为 1 时，表示连接左右两个方向，那么调用 detectL(x, y) 和 detectR(x, y) 两个函数。

这些函数的作用是什么呢？我们还是以 grid[x][y] = 1 为例子。当调用 detectL(x, y) 时，我们需要考虑左边的单元格 (x, y - 1)，这个单元格必须能够与它的右侧，即 (x, y) 相连，那么 grid[x][y - 1] 的值必须为 [1, 4, 6] 中的一个。因此在 detectL(x, y) 函数中，我们会先判断单元格 (x, y - 1) 是否存在，若存在，再判断 grid[x][y - 1] 的值是否满足要求。对于其余的三个函数，它们的作用也是类似的。

这样以来，我们遍历整个网格，对于其中的每一个单元格，根据它的 grid 值调用四个函数中的两个，并在满足要求时将该单元格与相邻的单元格相连（即在并查集中将它们合并）。在遍历结束之后，我们判断左上角和右下角在并查集中是否属于同一集合即可。

代码

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
class Solution {
public:
    static constexpr int MAX_N = 300 * 300 + 5;

    struct DisjointSet {
        int f[MAX_N];
        
        DisjointSet() {
            for (int i = 0; i < MAX_N; ++i) {
                f[i] = i;
            }
        }
        
        int find(int x) {
            return x == f[x] ? x : f[x] = find(f[x]);
        }
        
        void merge(int x, int y) {
            f[find(x)] = find(y);
        }
    } ds;
    
    bool hasValidPath(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        
        auto getId = [&] (int x, int y) {
            return x * n + y;
        };

        auto detectL = [&] (int x, int y) {
            if (y - 1 >= 0 && (grid[x][y - 1] == 4 || grid[x][y - 1] == 6 || grid[x][y - 1] == 1)) {
                ds.merge(getId(x, y), getId(x, y - 1));
            }
        };

        auto detectR = [&] (int x, int y) {
            if (y + 1 < n && (grid[x][y + 1] == 3 || grid[x][y + 1] == 5 || grid[x][y + 1] == 1)) {
                ds.merge(getId(x, y), getId(x, y + 1));
            }
        };

        auto detectU = [&] (int x, int y) {
            if (x - 1 >= 0 && (grid[x - 1][y] == 3 || grid[x - 1][y] == 4 || grid[x - 1][y] == 2)) {
                ds.merge(getId(x, y), getId(x - 1, y));
            }
        };

        auto detectD = [&] (int x, int y) {
            if (x + 1 < m && (grid[x + 1][y] == 5 || grid[x + 1][y] == 6 || grid[x + 1][y] == 2)) {
                ds.merge(getId(x, y), getId(x + 1, y));
            }
        };
        
        auto handler = [&] (int x, int y) {
            switch (grid[x][y]) {
                case 1: {
                    detectL(x, y); detectR(x, y);
                } break;
                case 2: {
                    detectU(x, y); detectD(x, y);
                } break;
                case 3: {
                    detectL(x, y); detectD(x, y);
                } break;
                case 4: {
                    detectR(x, y); detectD(x, y);
                } break;
                case 5: {
                    detectL(x, y); detectU(x, y);
                } break;
                case 6: {
                    detectR(x, y); detectU(x, y);
                }
            }
        };
        
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                handler(i, j);
            }
        }

        return ds.find(getId(0, 0)) == ds.find(getId(m - 1, n - 1));
    }
};
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
class Solution {
    class DisjointSet {
        int[] f;

        public DisjointSet(int m, int n) {
            f = new int[m * n];
            for (int i = 0; i < m * n; ++i) {
                f[i] = i;
            }
        }

        public int find(int x) {
            return x == f[x] ? x : (f[x] = find(f[x]));
        }
        
        public void merge(int x, int y) {
            f[find(x)] = find(y);
        }
    }

    int[][] grid;
    int m, n;
    DisjointSet ds;

    public boolean hasValidPath(int[][] grid) {
        this.grid = grid;
        m = grid.length;
        n = grid[0].length;
        ds = new DisjointSet(m, n);
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                handler(i, j);
            }
        }
        return ds.find(getId(0, 0)) == ds.find(getId(m - 1, n - 1));
    }

    public int getId(int x, int y) {
        return x * n + y;
    }

    public void detectL(int x, int y) {
        if (y - 1 >= 0 && (grid[x][y - 1] == 4 || grid[x][y - 1] == 6 || grid[x][y - 1] == 1)) {
            ds.merge(getId(x, y), getId(x, y - 1));
        }
    }

    public void detectR(int x, int y) {
        if (y + 1 < n && (grid[x][y + 1] == 3 || grid[x][y + 1] == 5 || grid[x][y + 1] == 1)) {
            ds.merge(getId(x, y), getId(x, y + 1));
        }
    }

    public void detectU(int x, int y) {
        if (x - 1 >= 0 && (grid[x - 1][y] == 3 || grid[x - 1][y] == 4 || grid[x - 1][y] == 2)) {
            ds.merge(getId(x, y), getId(x - 1, y));
        }
    }

    public void detectD(int x, int y) {
        if (x + 1 < m && (grid[x + 1][y] == 5 || grid[x + 1][y] == 6 || grid[x + 1][y] == 2)) {
            ds.merge(getId(x, y), getId(x + 1, y));
        }
    }

    public void handler(int x, int y) {
        switch (grid[x][y]) {
            case 1:
                detectL(x, y);
                detectR(x, y);
                break;
            case 2:
                detectU(x, y);
                detectD(x, y);
                break;
            case 3:
                detectL(x, y);
                detectD(x, y);
                break;
            case 4:
                detectR(x, y);
                detectD(x, y);
                break;
            case 5:
                detectL(x, y);
                detectU(x, y);
                break;
            case 6:
                detectR(x, y);
                detectU(x, y);
        }
    }
}
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
class Solution:
    class DisjointSet:
        def __init__(self, n):
            self.f = list(range(n))
        
        def find(self, x):
            if x == self.f[x]:
                return x
            self.f[x] = self.find(self.f[x])
            return self.f[x]
        
        def merge(self, x, y):
            self.f[self.find(x)] = self.find(y)

    def hasValidPath(self, grid: List[List[int]]) -> bool:
        m, n = len(grid), len(grid[0])
        ds = Solution.DisjointSet(m * n)

        def getId(x, y):
            return x * n + y
        
        def detectL(x, y):
            if y - 1 >= 0 and grid[x][y - 1] in [1, 4, 6]:
                ds.merge(getId(x, y), getId(x, y - 1))
        
        def detectR(x, y):
            if y + 1 < n and grid[x][y + 1] in [1, 3, 5]:
                ds.merge(getId(x, y), getId(x, y + 1))
        
        def detectU(x, y):
            if x - 1 >= 0 and grid[x - 1][y] in [2, 3, 4]:
                ds.merge(getId(x, y), getId(x - 1, y))
        
        def detectD(x, y):
            if x + 1 < m and grid[x + 1][y] in [2, 5, 6]:
                ds.merge(getId(x, y), getId(x + 1, y))

        def handler(x, y):
            if grid[x][y] == 1:
                detectL(x, y)
                detectR(x, y)
            elif grid[x][y] == 2:
                detectU(x, y)
                detectD(x, y)
            elif grid[x][y] == 3:
                detectL(x, y)
                detectD(x, y)
            elif grid[x][y] == 4:
                detectR(x, y)
                detectD(x, y)
            elif grid[x][y] == 5:
                detectL(x, y)
                detectU(x, y)
            else:
                detectR(x, y)
                detectU(x, y)
        
        for i in range(m):
            for j in range(n):
                handler(i, j)
        
        return ds.find(getId(0, 0)) == ds.find(getId(m - 1, n - 1))

复杂度分析

记单元格的总数为 t = m \times n。

  • 时间复杂度：这里的并查集使用了路径压缩，但是没有使用启发式合并，在最坏情况下单次操作的时间代价是 O(\log t)，平均情况下时间代价依然是 O(\alpha(t))，其中 \alpha 函数为阿克曼函数的反函数，增长比对数函数更加缓慢。t 个单元格每个最多和上下左右四个单元格中的两个做合并操作，所以平均情况下渐进时间复杂度为 O(t \times \alpha(t))。

  • 空间复杂度：并查集中 f 数组是辅助空间，长度为 t，故这里的渐进空间复杂度为 O(t)。

方法二：单元格性质建图

我们将四个方向进行编号：

1
2
3
4
5
6
7
     0
     ^
     |
3 <-- --> 1
     |
     v
     2

每一种单元格都可以用一个长度为 4 的二进制数表示，二进制数的第 i 位为 1 等价于该单元格在第 i 个方向存在街道。这样以来，每一种单元格对应的二进制数中都恰好有 2 个 1。

这样编号的好处是什么呢？可以发现，只有在这些情况下，两个相邻的单元格才能相连：

  • 如果某一个单元格有第 0 个方向，那么它上方的单元格必须有第 2 个方向；

  • 如果某一个单元格有第 1 个方向，那么它右侧的单元格必须有第 3 个方向；

  • 如果某一个单元格有第 2 个方向，那么它下方的单元格必须有第 0 个方向；

  • 如果某一个单元格有第 3 个方向，那么它左侧的单元格必须有第 1 个方向。

发现了什么规律？

如果某一个单元格有第 i 个方向，那么它在第 i 个方向相邻的单元格必须有第 (i + 2) % 4 个方向。

因此，我们遍历整个网格，对于其中的每一个单元格 (x, y)，我们枚举它的四个相邻的单元格，对于第 i 个方向的相邻单元格，它和 (x, y) 相连当且仅当 (x, y) 对应的二进制数的第 i 位和相邻单元格对应的二进制数的第 (i + 2) % 4 位均为 1。在遍历结束之后，我们判断左上角和右下角在并查集中是否属于同一集合即可。

[sol2-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class Solution {
public:
    static constexpr int MAX_N = 300 * 300 + 5;
    static constexpr int patterns[7] = {0, 0b1010, 0b0101, 0b1100, 0b0110, 0b1001, 0b0011};
    static constexpr int dirs[4][2] = { {-1, 0}, {0, 1}, {1, 0}, {0, -1} };

    struct DisjointSet {
        int f[MAX_N];
        
        DisjointSet() {
            for (int i = 0; i < MAX_N; ++i) f[i] = i;
        }
        
        int find(int x) {
            return x == f[x] ? x : f[x] = find(f[x]);
        }
        
        void merge(int x, int y) {
            f[find(x)] = find(y);
        }
    } ds;
    
    bool hasValidPath(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        
        auto getId = [&] (int x, int y) {
            return x * n + y;
        };

        auto handler = [&] (int x, int y) {
            int pattern = patterns[grid[x][y]];
            for (int i = 0; i < 4; ++i) {
                if (pattern & (1 << i)) {
                    int sx = x + dirs[i][0];
                    int sy = y + dirs[i][1];
                    if (sx >= 0 && sx < m && sy >= 0 && sy < n and (patterns[grid[sx][sy]] & (1 << ((i + 2) % 4)))) {
                        ds.merge(getId(x, y), getId(sx, sy));
                    }
                }
            }
        };
        
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                handler(i, j);
            }
        }

        return ds.find(getId(0, 0)) == ds.find(getId(m - 1, n - 1));
    }
};
[sol2-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
class Solution {
    class DisjointSet {
        int[] f;

        public DisjointSet(int m, int n) {
            f = new int[m * n];
            for (int i = 0; i < m * n; ++i) {
                f[i] = i;
            }
        }

        public int find(int x) {
            return x == f[x] ? x : (f[x] = find(f[x]));
        }
        
        public void merge(int x, int y) {
            f[find(x)] = find(y);
        }
    }

    int[] patterns = {0, 0b1010, 0b0101, 0b1100, 0b0110, 0b1001, 0b0011};
    int[][] dirs = { {-1, 0}, {0, 1}, {1, 0}, {0, -1} };
    int[][] grid;
    int m, n;
    DisjointSet ds;

    public boolean hasValidPath(int[][] grid) {
        this.grid = grid;
        m = grid.length;
        n = grid[0].length;
        ds = new DisjointSet(m, n);
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                handler(i, j);
            }
        }
        return ds.find(getId(0, 0)) == ds.find(getId(m - 1, n - 1));
    }

    public int getId(int x, int y) {
        return x * n + y;
    }

    public void handler(int x, int y) {
        int pattern = patterns[grid[x][y]];
        for (int i = 0; i < 4; ++i) {
            if ((pattern & (1 << i)) != 0) {
                int sx = x + dirs[i][0];
                int sy = y + dirs[i][1];
                if (sx >= 0 && sx < m && sy >= 0 && sy < n && (patterns[grid[sx][sy]] & (1 << ((i + 2) % 4))) != 0) {
                    ds.merge(getId(x, y), getId(sx, sy));
                }
            }
        }
    }
}
[sol2-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution:
    class DisjointSet:
        def __init__(self, n):
            self.f = list(range(n))
        
        def find(self, x):
            if x == self.f[x]:
                return x
            self.f[x] = self.find(self.f[x])
            return self.f[x]
        
        def merge(self, x, y):
            self.f[self.find(x)] = self.find(y)

    def hasValidPath(self, grid: List[List[int]]) -> bool:
        m, n = len(grid), len(grid[0])
        patterns = [0, 0b1010, 0b0101, 0b1100, 0b0110, 0b1001, 0b0011]
        dirs = [(-1, 0), (0, 1), (1, 0), (0, -1)]
        ds = Solution.DisjointSet(m * n)
        
        def getId(x, y):
            return x * n + y

        def handler(x, y):
            pattern = patterns[grid[x][y]]
            for i, (dx, dy) in enumerate(dirs):
                if (pattern & (1 << i)) > 0:
                    sx, sy = x + dx, y + dy
                    if 0 <= sx < m and 0 <= sy < n and (patterns[grid[sx][sy]] & (1 << ((i + 2) % 4))) > 0:
                        ds.merge(getId(x, y), getId(sx, sy))
        
        for i in range(m):
            for j in range(n):
                handler(i, j)
        
        return ds.find(getId(0, 0)) == ds.find(getId(m - 1, n - 1))

复杂度分析

方法二相较于方法一只在建图时的判断方法有差异，由于两种判断方法的时间复杂度均为 O(1)，因此时空复杂度均与方法一一致。

 Comments
On this page
1391-检查网格中是否存在有效路径