1411-给 N x 3 网格图涂色的方案数

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:29 2023-09-13 16:06:29 Updated    

你有一个 n x 3 的网格图 grid ，你需要用 红，黄，绿
三种颜色之一给每一个格子上色，且确保相邻格子颜色不同（也就是有相同水平边或者垂直边的格子颜色不同）。

给你网格图的行数 n 。

请你返回给 grid 涂色的方案数。由于答案可能会非常大，请你返回答案对 10^9 + 7 取余的结果。

示例 1：

**输入：** n = 1
**输出：** 12
**解释：** 总共有 12 种可行的方法：
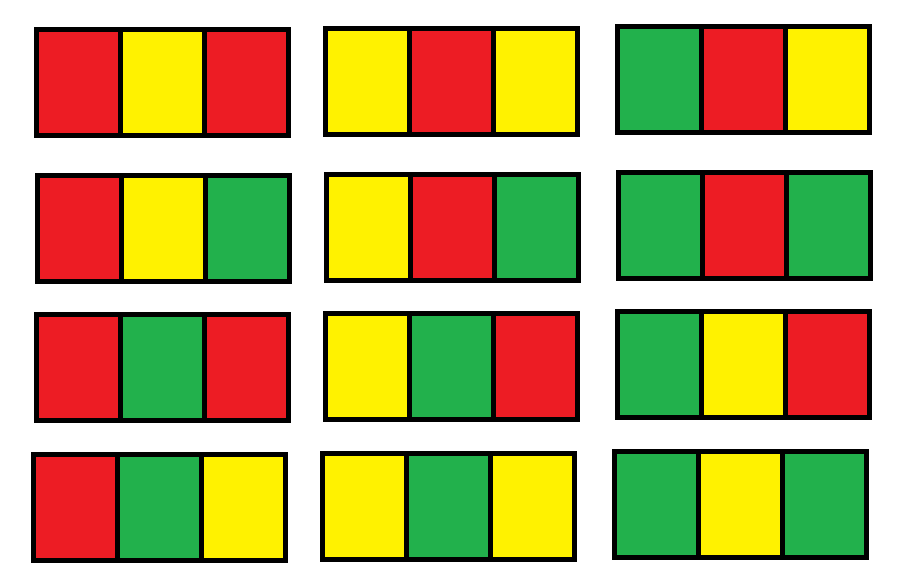
![](https://assets.leetcode-cn.com/aliyun-lc-upload/uploads/2020/04/12/e1.png)

示例 2：

**输入：** n = 2
**输出：** 54

示例 3：

**输入：** n = 3
**输出：** 246

示例 4：

**输入：** n = 7
**输出：** 106494

示例 5：

**输入：** n = 5000
**输出：** 30228214

提示：

  • n == grid.length
  • grid[i].length == 3
  • 1 <= n <= 5000

方法一：递推

我们可以用 f[i][\textit{type}] 表示当网格的大小为 i \times 3 且最后一行的填色方法为 type 时的方案数。由于我们在填充第 i 行时，会影响我们填充方案的只有它上面的那一行（即 i - 1 行），因此用 f[i][\textit{type}] 表示状态是合理的。

那么我们如何计算 f[i][\textit{type}] 呢？可以发现：

  • 首先，type 本身是要满足要求的。每一行有 3 个网格，如果我们用 0, 1, 2 分别代表红黄绿，那么 type 可以看成一个三进制数，例如 type} = (102)_3 时，表示 3 个网格从左到右的颜色分别为黄、红、绿；

    • 这样以来，我们可以预处理出所有满足要求的 type。具体地，我们使用三重循环分别枚举每一个格子的颜色，只有相邻的格子颜色不相同时，type 才满足要求。

  • 其次，f[i][\textit{type}] 应该等于所有 f[i - 1][\textit{type}’] 的和，其中 type’ 和 type 可以作为相邻的行。也就是说，type’ 和 type 的对应位置不能相同。

递推解法的本身不难想出，难度在于上述的预处理以及编码实现。下面给出包含详细注释的 C++、Java 和 Python 代码。

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
class Solution {
private:
    static constexpr int mod = 1000000007;

public:
    int numOfWays(int n) {
        // 预处理出所有满足条件的 type
        vector<int> types;
        for (int i = 0; i < 3; ++i) {
            for (int j = 0; j < 3; ++j) {
                for (int k = 0; k < 3; ++k) {
                    if (i != j && j != k) {
                        // 只要相邻的颜色不相同就行
                        // 将其以十进制的形式存储
                        types.push_back(i * 9 + j * 3 + k);
                    }
                }
            }
        }
        int type_cnt = types.size();
        // 预处理出所有可以作为相邻行的 type 对
        vector<vector<int>> related(type_cnt, vector<int>(type_cnt));
        for (int i = 0; i < type_cnt; ++i) {
            // 得到 types[i] 三个位置的颜色
            int x1 = types[i] / 9, x2 = types[i] / 3 % 3, x3 = types[i] % 3;
            for (int j = 0; j < type_cnt; ++j) {
                // 得到 types[j] 三个位置的颜色
                int y1 = types[j] / 9, y2 = types[j] / 3 % 3, y3 = types[j] % 3;
                // 对应位置不同色，才能作为相邻的行
                if (x1 != y1 && x2 != y2 && x3 != y3) {
                    related[i][j] = 1;
                }
            }
        }
        // 递推数组
        vector<vector<int>> f(n + 1, vector<int>(type_cnt));
        // 边界情况，第一行可以使用任何 type
        for (int i = 0; i < type_cnt; ++i) {
            f[1][i] = 1;
        }
        for (int i = 2; i <= n; ++i) {
            for (int j = 0; j < type_cnt; ++j) {
                for (int k = 0; k < type_cnt; ++k) {
                    // f[i][j] 等于所有 f[i - 1][k] 的和
                    // 其中 k 和 j 可以作为相邻的行
                    if (related[k][j]) {
                        f[i][j] += f[i - 1][k];
                        f[i][j] %= mod;
                    }
                }
            }
        }
        // 最终所有的 f[n][...] 之和即为答案
        int ans = 0;
        for (int i = 0; i < type_cnt; ++i) {
            ans += f[n][i];
            ans %= mod;
        }
        return ans;
    }
};
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
class Solution {
    static final int MOD = 1000000007;

    public int numOfWays(int n) {
        // 预处理出所有满足条件的 type
        List<Integer> types = new ArrayList<Integer>();
        for (int i = 0; i < 3; ++i) {
            for (int j = 0; j < 3; ++j) {
                for (int k = 0; k < 3; ++k) {
                    if (i != j && j != k) {
                        // 只要相邻的颜色不相同就行
                        // 将其以十进制的形式存储
                        types.add(i * 9 + j * 3 + k);
                    }
                }
            }
        }
        int typeCnt = types.size();
        // 预处理出所有可以作为相邻行的 type 对
        int[][] related = new int[typeCnt][typeCnt];
        for (int i = 0; i < typeCnt; ++i) {
            // 得到 types[i] 三个位置的颜色
            int x1 = types.get(i) / 9, x2 = types.get(i) / 3 % 3, x3 = types.get(i) % 3;
            for (int j = 0; j < typeCnt; ++j) {
                // 得到 types[j] 三个位置的颜色
                int y1 = types.get(j) / 9, y2 = types.get(j) / 3 % 3, y3 = types.get(j) % 3;
                // 对应位置不同色，才能作为相邻的行
                if (x1 != y1 && x2 != y2 && x3 != y3) {
                    related[i][j] = 1;
                }
            }
        }
        // 递推数组
        int[][] f = new int[n + 1][typeCnt];
        // 边界情况，第一行可以使用任何 type
        for (int i = 0; i < typeCnt; ++i) {
            f[1][i] = 1;
        }
        for (int i = 2; i <= n; ++i) {
            for (int j = 0; j < typeCnt; ++j) {
                for (int k = 0; k < typeCnt; ++k) {
                    // f[i][j] 等于所有 f[i - 1][k] 的和
                    // 其中 k 和 j 可以作为相邻的行
                    if (related[k][j] != 0) {
                        f[i][j] += f[i - 1][k];
                        f[i][j] %= MOD;
                    }
                }
            }
        }
        // 最终所有的 f[n][...] 之和即为答案
        int ans = 0;
        for (int i = 0; i < typeCnt; ++i) {
            ans += f[n][i];
            ans %= MOD;
        }
        return ans;
    }
}
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution:
    def numOfWays(self, n: int) -> int:
        mod = 10**9 + 7
        # 预处理出所有满足条件的 type
        types = list()
        for i in range(3):
            for j in range(3):
                for k in range(3):
                    if i != j and j != k:
                        # 只要相邻的颜色不相同就行
                        # 将其以十进制的形式存储
                        types.append(i * 9 + j * 3 + k)
        type_cnt = len(types)
        # 预处理出所有可以作为相邻行的 type 对
        related = [[0] * type_cnt for _ in range(type_cnt)]
        for i, ti in enumerate(types):
            # 得到 types[i] 三个位置的颜色
            x1, x2, x3 = ti // 9, ti // 3 % 3, ti % 3
            for j, tj in enumerate(types):
                # 得到 types[j] 三个位置的颜色
                y1, y2, y3 = tj // 9, tj // 3 % 3, tj % 3
                # 对应位置不同色，才能作为相邻的行
                if x1 != y1 and x2 != y2 and x3 != y3:
                    related[i][j] = 1
        # 递推数组
        f = [[0] * type_cnt for _ in range(n + 1)]
        # 边界情况，第一行可以使用任何 type
        f[1] = [1] * type_cnt
        for i in range(2, n + 1):
            for j in range(type_cnt):
                for k in range(type_cnt):
                    # f[i][j] 等于所有 f[i - 1][k] 的和
                    # 其中 k 和 j 可以作为相邻的行
                    if related[k][j]:
                        f[i][j] += f[i - 1][k]
                        f[i][j] %= mod
        # 最终所有的 f[n][...] 之和即为答案
        ans = sum(f[n]) % mod
        return ans

复杂度分析

  • 时间复杂度：O(T^2N)，其中 T 是满足要求的 type 的数量，在示例一中已经给出了 T = 12。在递推的过程中，我们需要计算所有的 f[i][\textit{type}]，并且需要枚举上一行的 type}’。

  • 空间复杂度：O(T^2 + TN)。我们需要 T * T 的二维数组存储 type 之间的关系，T * N 的数组存储递推的结果。注意到由于 f[i][\textit{type}] 只和上一行的状态有关，我们可以使用两个一维数组存储当前行和上一行的 f 值，空间复杂度降低至 O(T^2 + 2T) = O(T^2)。

方法二：递推优化

如果读者有一些高中数学竞赛基础，就可以发现上面的这个递推式是线性的，也就是说：

  • 我们可以进行一些化简；

  • 它存在通项公式。

直观上，我们怎么化简方法一中的递推呢？

我们把满足要求的 type 都写出来，一共有 12 种：

1
010, 012, 020, 021, 101, 102, 120, 121, 201, 202, 210, 212

我们可以把它们分成两类：

  • ABC 类：三个颜色互不相同，一共有 6 种：012, 021, 102, 120, 201, 210；

  • ABA 类：左右两侧的颜色相同，也有 6 种：010, 020, 101, 121, 202, 212。

这样我们就可以把 12 种 type 浓缩成了 2 种，尝试写出这两类之间的递推式。我们用 f[i][0] 表示 ABC 类，f[i][1] 表示 ABA 类。在计算时，我们可以将任意一种满足要求的涂色方法带入第 i - 1 行，并检查第 i 行的方案数，这是因为同一类的涂色方法都是等价的：

  • 第 i - 1 行是 ABC 类，第 i 行是 ABC 类：以 012 为例，那么第 i 行只能是120 或 201，方案数为 2；

  • 第 i - 1 行是 ABC 类，第 i 行是 ABA 类：以 012 为例，那么第 i 行只能是 101 或 121，方案数为 2；

  • 第 i - 1 行是 ABA 类，第 i 行是 ABC 类：以 010 为例，那么第 i 行只能是 102 或 201，方案数为 2；

  • 第 i - 1 行是 ABA 类，第 i 行是 ABA 类：以 010 为例，那么第 i 行只能是 101，121 或 202，方案数为 3。

因此我们就可以写出递推式：

\begin{cases}
f[i][0] = 2 * f[i - 1][0] + 2 * f[i - 1][1] \
f[i][1] = 2 * f[i - 1][0] + 3 * f[i - 1][1]
\end{cases}

[sol2-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
private:
    static constexpr int mod = 1000000007;

public:
    int numOfWays(int n) {
        int fi0 = 6, fi1 = 6;
        for (int i = 2; i <= n; ++i) {
            int new_fi0 = (2LL * fi0 + 2LL * fi1) % mod;
            int new_fi1 = (2LL * fi0 + 3LL * fi1) % mod;
            fi0 = new_fi0;
            fi1 = new_fi1;
        }
        return (fi0 + fi1) % mod;
    }
};
[sol2-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    static final int MOD = 1000000007;

    public int numOfWays(int n) {
        long fi0 = 6, fi1 = 6;
        for (int i = 2; i <= n; ++i) {
            long newFi0 = (2 * fi0 + 2 * fi1) % MOD;
            long newFi1 = (2 * fi0 + 3 * fi1) % MOD;
            fi0 = newFi0;
            fi1 = newFi1;
        }
        return (int) ((fi0 + fi1) % MOD);
    }
}
[sol2-Python3]
1
2
3
4
5
6
7
class Solution:
    def numOfWays(self, n: int) -> int:
        mod = 10**9 + 7
        fi0, fi1 = 6, 6
        for i in range(2, n + 1):
            fi0, fi1 = (2 * fi0 + 2 * fi1) % mod, (2 * fi0 + 3 * fi1) % mod
        return (fi0 + fi1) % mod

复杂度分析

  • 时间复杂度：O(N)。

  • 空间复杂度：O(1)。

 Comments
On this page
1411-给 N x 3 网格图涂色的方案数