1453-圆形靶内的最大飞镖数量

Alice 向一面非常大的墙上掷出 n 支飞镖。给你一个数组 darts ，其中 darts[i] = [xi, yi] 表示 Alice
掷出的第 i 支飞镖落在墙上的位置。

Bob 知道墙上所有 n 支飞镖的位置。他想要往墙上放置一个半径为 r 的圆形靶。使 Alice 掷出的飞镖尽可能多地落在靶上。

给你整数 r ，请返回能够落在 任意 半径为 r 的圆形靶内或靶上的最大飞镖数。

示例 1 ：

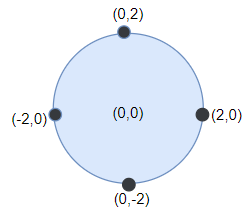
**输入：** darts = [[-2,0],[2,0],[0,2],[0,-2]], r = 2
**输出：** 4
**解释：** 如果圆形靶的圆心为 (0,0) ，半径为 2 ，所有的飞镖都落在靶上，此时落在靶上的飞镖数最大，值为 4 。

示例 2 ：

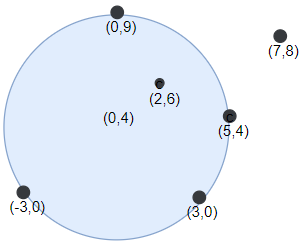
**输入：** darts = [[-3,0],[3,0],[2,6],[5,4],[0,9],[7,8]], r = 5
**输出：** 5
**解释：** 如果圆形靶的圆心为 (0,4) ，半径为 5 ，则除了 (7,8) 之外的飞镖都落在靶上，此时落在靶上的飞镖数最大，值为 5 。

提示：

• 1 <= darts.length <= 100
• darts[i].length == 2
• -104 <= xi, yi <= 104
• darts 中的元素互不相同
• 1 <= r <= 5000

题意

本题就是要计算给定半径，圆心不定，然后算圆内的点数最多是多少
我们可以通过两点确定一个圆心，穷举所有的圆心即可。

计算圆心

先给一张图：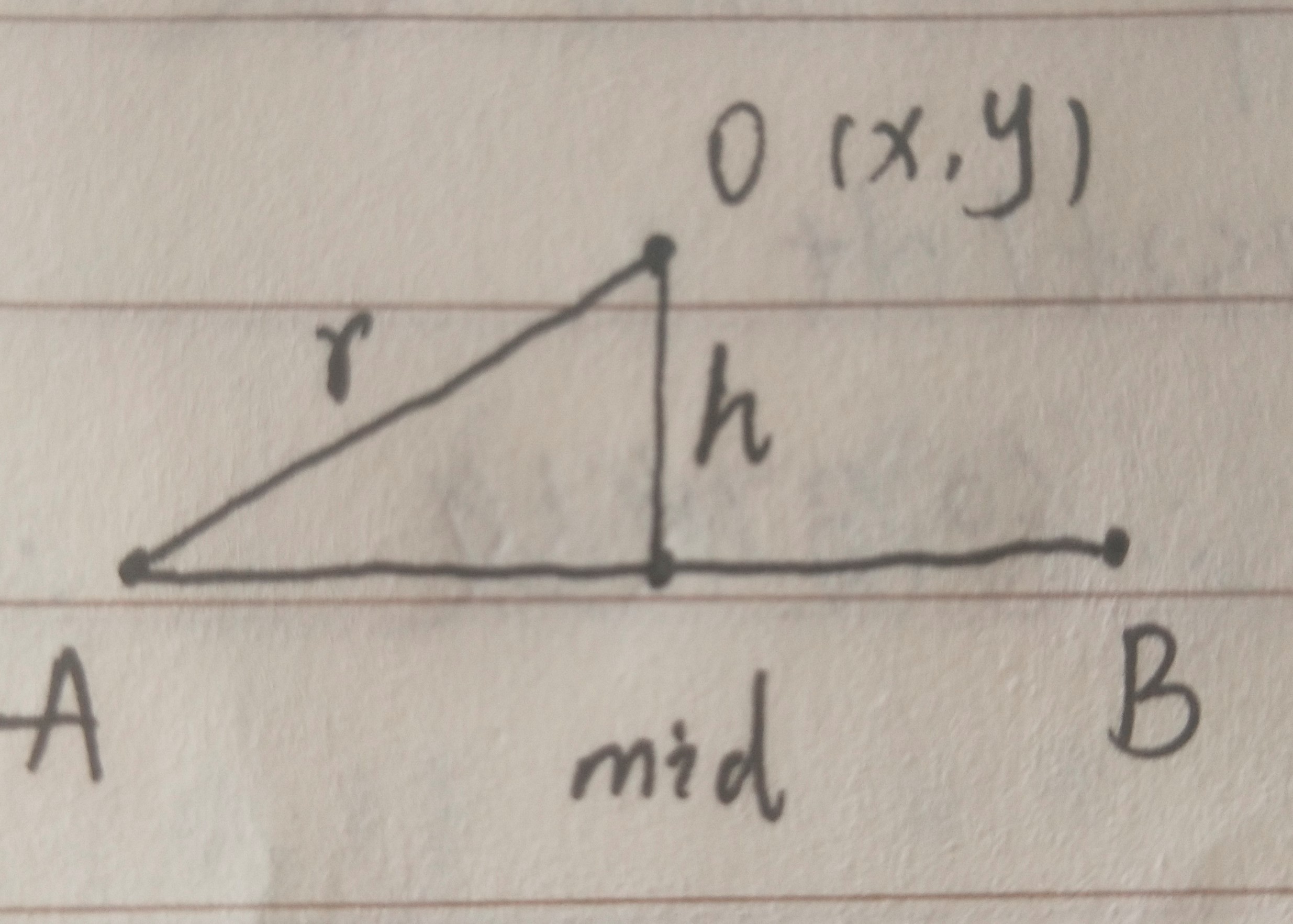

给定A(x1,y1) B(x2,y2) 以及圆心r
首先就可以直接计算出垂线长度h和mid坐标(AB中点)以及AB长度d:

d=sqrt((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1));
h=sqrt(r*r-(d/2.0)*(d/2.0))
mid=((x1+x2)/2.0,(y1+y2)/2.0)

然后我们的目的是求O(x,y)

我们使用向量。
看这个图：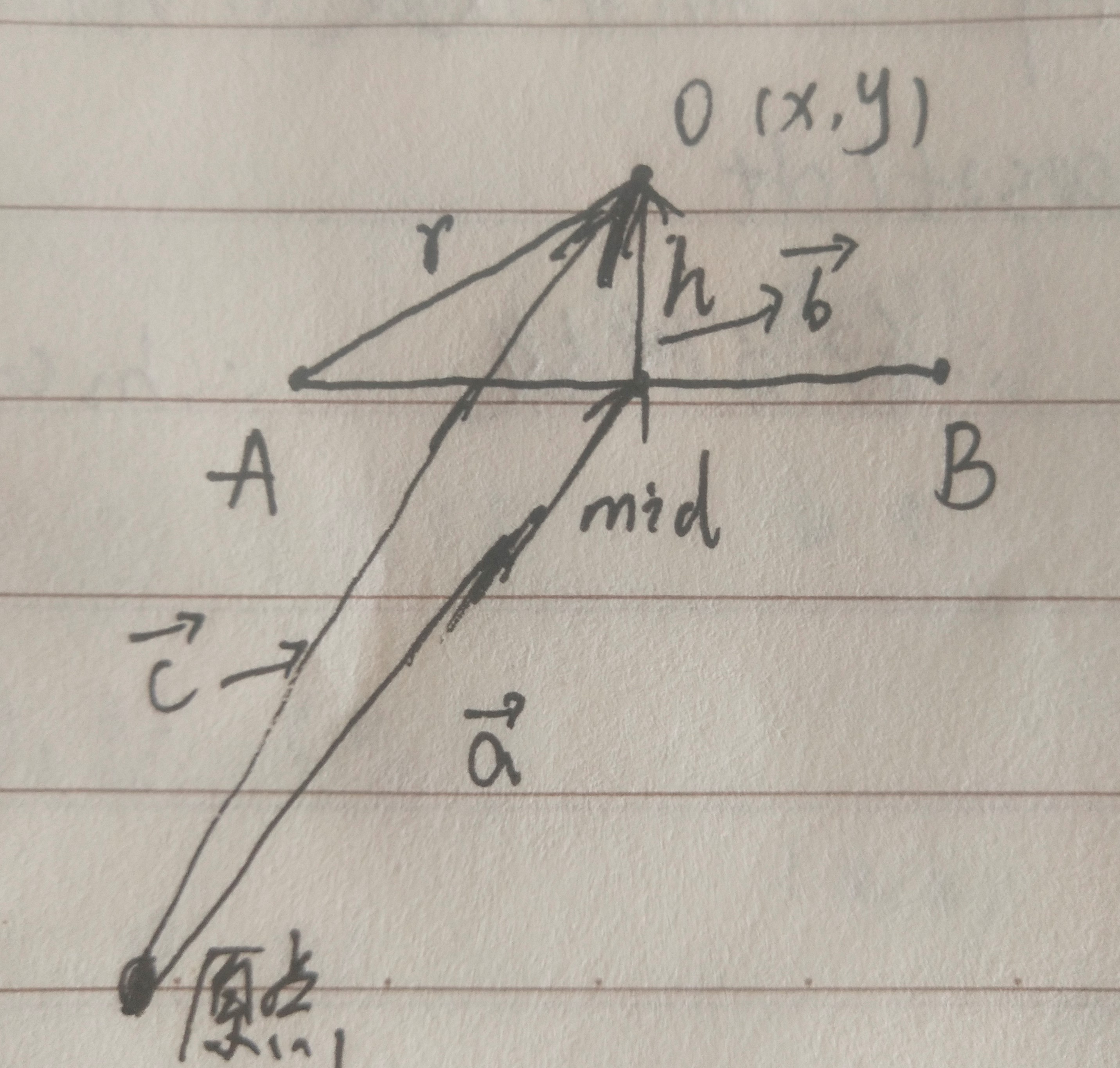

向量a+向量b=向量c
毫无疑问
向量a就是mid坐标，向量b就是AB垂线的单位方向向量乘以高度h，向量c就是O坐标

所以现在唯一的问题就在于如何计算AB垂线的方向向量
向量AB=(x3,y3) 垂线的向量即为(-y3,x3)和(y3,-x3)
点积为0

特殊情况，AB长度大于2*r (d>2r) ，此时不存在圆心

还不明白的可以看一下代码，就会了：

代码

经@灵茶山艾府 指正，因为我穷举a b后还会穷举b a,所以每组只用计算一个圆心即可。
另一个方向的圆心会在第二次枚举的时候被计算出来。

struct point{
    double x,y;
    point(double i,double j):x(i),y(j){}
};

//算两点距离
double dist(double x1,double y1,double x2,double y2){
    return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}

//计算圆心
point f(point& a,point& b,int r){
    //算中点
    point mid((a.x+b.x)/2.0,(a.y+b.y)/2.0);
    //AB距离的一半
    double d=dist(a.x,a.y,mid.x,mid.y);
    //计算h
    double h=sqrt(r*r-d*d);
    //计算垂线
    point ba(b.x-a.x,b.y-a.y);
    point hd(-ba.y,ba.x);
    double len=sqrt(hd.x*hd.x+hd.y*hd.y);
    hd.x/=len,hd.y/=len;
    hd.x*=h,hd.y*=h;
    return point(hd.x+mid.x,hd.y+mid.y);
}

class Solution {
public:
    int numPoints(vector<vector<int>>& points, int r) {
        int n=points.size();
        int ans=0;
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                if(i==j){//一个点
                    int cnt=0;
                    for(int k=0;k<n;k++){
                        double tmp=dist(points[i][0],points[i][1],points[k][0],points[k][1]);
                        if(tmp<=r) cnt++;
                    }
                    ans=max(cnt,ans);
                }else{//两个点
                    //通过长度判断有没有圆心
                    double d=dist(points[i][0],points[i][1],points[j][0],points[j][1]);
                    if(d/2>r) continue;

                    point a(points[i][0],points[i][1]),b(points[j][0],points[j][1]);
                    point res=f(a,b,r);
                    int cnt=0;
                    for(int k=0;k<n;k++){
                        double tmp=dist(res.x,res.y,points[k][0],points[k][1]);
                        if(tmp<=r) cnt++;
                    }
                    ans=max(cnt,ans);
                }
            }
        }
        return ans;
    }
};

总结

计算圆心也是有别的方法的，在此仅分享这一种
求个赞