1457-二叉树中的伪回文路径
给你一棵二叉树,每个节点的值为 1 到 9 。我们称二叉树中的一条路径是 「 伪回文
」的,当它满足:路径经过的所有节点值的排列中,存在一个回文序列。
请你返回从根到叶子节点的所有路径中 **伪回文 **路径的数目。
示例 1:
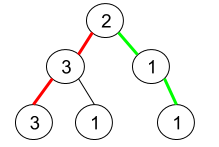
**输入:** root = [2,3,1,3,1,null,1]
**输出:** 2
**解释:** 上图为给定的二叉树。总共有 3 条从根到叶子的路径:红色路径 [2,3,3] ,绿色路径 [2,1,1] 和路径 [2,3,1] 。
在这些路径中,只有红色和绿色的路径是伪回文路径,因为红色路径 [2,3,3] 存在回文排列 [3,2,3] ,绿色路径 [2,1,1] 存在回文排列 [1,2,1] 。
示例 2:
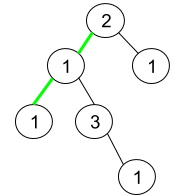
**输入:** root = [2,1,1,1,3,null,null,null,null,null,1]
**输出:** 1
**解释:** 上图为给定二叉树。总共有 3 条从根到叶子的路径:绿色路径 [2,1,1] ,路径 [2,1,3,1] 和路径 [2,1] 。
这些路径中只有绿色路径是伪回文路径,因为 [2,1,1] 存在回文排列 [1,2,1] 。
示例 3:
**输入:** root = [9]
**输出:** 1
提示:
- 给定二叉树的节点数目在范围
[1, 105]内 1 <= Node.val <= 9
Problem: 1457. 二叉树中的伪回文路径
[TOC]
思路
- 回溯,进行深度优先遍历(dfs)时,同时将路径的值使用位运算从起始0开始,依次与1左移节点val位的值进行异或运算,回溯记录每个路径的最终值。
- 这个位运算记录的究竟是什么值呢?我们首先要知道回文如何组成:1、所有的数的个数都是偶数的;2、存在一个数是奇数,其他数都是偶数的。
- 又由于val的值域很小,那我们可以用位运算来统计,位运算的位代表节点的值,重复的数会在同一位上进行异或,偶数其会变成0,是奇数时会变成1。
- 最后路径得到的数num,只要其二进制位上没有1或者只有一个1则代表是回文。
- 那么怎么判断呢?二进制上没有1,则其是0,很好判断。只有一个1的情况我们可以使用(num & (num - 1)) === 0来判断,这个也很好理解,只有一个1比如10000,其-1会的到01111,每一位使用&则全部变成0,所有二进制只有一个1的情况都如此,10与01,100与011,以此类推。
Code
1 |
|
Comments