1458-两个子序列的最大点积

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:25 2023-09-13 16:06:25 Updated    

给你两个数组 nums1 和 nums2 。

请你返回 nums1 和 nums2 中两个长度相同的 非空 子序列的最大点积。

数组的非空子序列是通过删除原数组中某些元素（可能一个也不删除）后剩余数字组成的序列，但不能改变数字间相对顺序。比方说，[2,3,5] 是
[1,2,3,4,5] 的一个子序列而 [1,5,3] 不是。

示例 1：

**输入：** nums1 = [2,1,-2,5], nums2 = [3,0,-6]
**输出：** 18
**解释：** 从 nums1 中得到子序列 [2,-2] ，从 nums2 中得到子序列 [3,-6] 。
它们的点积为 (2*3 + (-2)*(-6)) = 18 。

示例 2：

**输入：** nums1 = [3,-2], nums2 = [2,-6,7]
**输出：** 21
**解释：** 从 nums1 中得到子序列 [3] ，从 nums2 中得到子序列 [7] 。
它们的点积为 (3*7) = 21 。

示例 3：

**输入：** nums1 = [-1,-1], nums2 = [1,1]
**输出：** -1
**解释：** 从 nums1 中得到子序列 [-1] ，从 nums2 中得到子序列 [1] 。
它们的点积为 -1 。

提示：

  • 1 <= nums1.length, nums2.length <= 500
  • -1000 <= nums1[i], nums2[i] <= 100

点积：

定义 **a**  = [ _a_ 1,  _a_ 2,…,  _a_ _n_ ] 和 **b** = [ _b_ 1,  _b_ 2,…,  _b_ _n_ ] 的点积为：

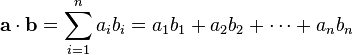
![\\mathbf{a}\\cdot \\mathbf{b} = \\sum_{i=1}^n a_ib_i = a_1b_1 + a_2b_2 + \\cdots + a_nb_n ](https://pic.leetcode-cn.com/1666164309-PBJMQp-image.png)

这里的 **Σ** 指示总和符号。

方法一：动态规划

我们用 f[i][j] 表示只考虑数组 nums}_1 的前 i 个元素以及数组 nums}_2 的前 j 个元素时，可以得到的两个长度相同的非空子序列的最大点积。这里元素的下标从 0 开始计数，与题目描述保持一致。

那么如何进行状态转移呢？我们可以考虑每个数组中的最后一个元素：

  • 如果我们选择了 nums}_1[i] 以及 nums}2[j] 并将它们形成点积，那么这一对数字对答案的贡献为 x{ij} = \textit{nums}_1[i] * \textit{nums}_2[j]。在选择了这一对数字之后，前面还有 nums}_1 的前 i-1 个元素以及数组 nums}2 的前 j-1 个元素，我们可以在其中选择数字对，也可以不选择，因为题目描述中唯一的限制就是「选择的子序列」非空，而我们已经选择了 x{ij 这一数字对。

    • 如果我们在前面的元素中选择数字对，那么最大点积即为 f[i-1][j-1] + x_{ij；

    • 如果我们不选择其它的数字对，那么最大点积即为 x_{ij。

  • 如果我们没有选择 nums}_1[i] 以及 nums}_2[j] 形成点积，由于它们是各自数组的最后一个元素，因此其中至少有一个不会与其它的任意元素形成点积。

    如果 nums}_1[i] 与 nums}_2[j_0] 形成点积，而 nums}_2[j] 与 nums}_1[i_0] 形成点积，那么不失一般性，必须保证 i < i_0 且 j_0 < j，即不改变数字间相对有序，然而 nums}[i] 是数组中的最后一个元素，因此 i_0 不存在，产生了矛盾。

    这样我们可以「扔掉」nums}_1[i] 和 nums}_2[j] 中的至少一个元素：

    • 如果扔掉 nums}_1[i]，那么最大点积即为 f[i-1][j]；

    • 如果扔掉 nums}_2[j]，那么最大点积即为 f[i][j-1]；

    • 如果同时扔掉 nums}_1[i] 和 nums}_2[j]，那么最大点积即为 f[i-1][j-1]。

根据上面的分析，我们就可以写出状态转移方程；

f[i][j] = \max(f[i-1][j-1] + x_{ij}, x_{ij}, f[i-1][j], f[i][j-1], f[i-1][j-1])

注意到状态转移方程中有一个可以优化的地方，这是因为 f[i-1][j] 以及 f[i][j-1] 对应的状态转移方程中已经包含了 f[i-1][j-1]，因此可以从状态转移方程中移除这一项，即：

f[i][j] = \max(f[i-1][j-1] + x_{ij}, x_{ij}, f[i-1][j], f[i][j-1])

动态规划的边界条件也非常容易处理。在对 f[i][j] 进行转移时，我们只要处理那些没有超出边界的项就行了。最后的答案即为 f[m-1][n-1]，其中 m 和 n 分别是数组 nums}_1 以及数组 nums}_2 的长度。

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int maxDotProduct(vector<int>& nums1, vector<int>& nums2) {
        int m = nums1.size();
        int n = nums2.size();
        vector<vector<int>> f(m, vector<int>(n));

        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                int xij = nums1[i] * nums2[j];
                f[i][j] = xij;
                if (i > 0) {
                    f[i][j] = max(f[i][j], f[i - 1][j]);
                }
                if (j > 0) {
                    f[i][j] = max(f[i][j], f[i][j - 1]);
                }
                if (i > 0 && j > 0) {
                    f[i][j] = max(f[i][j], f[i - 1][j - 1] + xij);
                }
            }
        }

        return f[m - 1][n - 1];
    }
};
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution:
    def maxDotProduct(self, nums1: List[int], nums2: List[int]) -> int:
        m, n = len(nums1), len(nums2)
        f = [[0] * n for _ in range(m)]
        
        for i in range(m):
            for j in range(n):
                xij = nums1[i] * nums2[j]
                f[i][j] = xij
                if i > 0:
                    f[i][j] = max(f[i][j], f[i - 1][j])
                if j > 0:
                    f[i][j] = max(f[i][j], f[i][j - 1])
                if i > 0 and j > 0:
                    f[i][j] = max(f[i][j], f[i - 1][j - 1] + xij)
        
        return f[m - 1][n - 1]
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int maxDotProduct(int[] nums1, int[] nums2) {
        int m = nums1.length;
        int n = nums2.length;
        int[][] f = new int[m][n];

        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                int xij = nums1[i] * nums2[j];
                f[i][j] = xij;
                if (i > 0) {
                    f[i][j] = Math.max(f[i][j], f[i - 1][j]);
                }
                if (j > 0) {
                    f[i][j] = Math.max(f[i][j], f[i][j - 1]);
                }
                if (i > 0 && j > 0) {
                    f[i][j] = Math.max(f[i][j], f[i - 1][j - 1] + xij);
                }
            }
        }

        return f[m - 1][n - 1];
    }
}

复杂度分析

  • 时间复杂度：O(mn)，其中 m 和 n 分别是数组 nums}_1 以及数组 nums}_2 的长度。

  • 空间复杂度：O(mn)，用来存储所有的状态。注意到 f[i][j] 只会从 f[i][..] 以及 f[i-1][..] 转移而来，因此我们可以使用两个一维数组交替地进行状态转移，时间复杂度降低为 O(n)。

 Comments
On this page
1458-两个子序列的最大点积