1463-摘樱桃 II

给你一个 rows x cols 的矩阵 grid 来表示一块樱桃地。 grid 中每个格子的数字表示你能获得的樱桃数目。

你有两个机器人帮你收集樱桃，机器人 1 从左上角格子 (0,0) 出发，机器人 2 从右上角格子 (0, cols-1) 出发。

请你按照如下规则，返回两个机器人能收集的最多樱桃数目：

从格子 (i,j) 出发，机器人可以移动到格子 (i+1, j-1)，(i+1, j) 或者 (i+1, j+1) 。
当一个机器人经过某个格子时，它会把该格子内所有的樱桃都摘走，然后这个位置会变成空格子，即没有樱桃的格子。
当两个机器人同时到达同一个格子时，它们中只有一个可以摘到樱桃。
两个机器人在任意时刻都不能移动到 grid 外面。
两个机器人最后都要到达 grid 最底下一行。

示例 1：

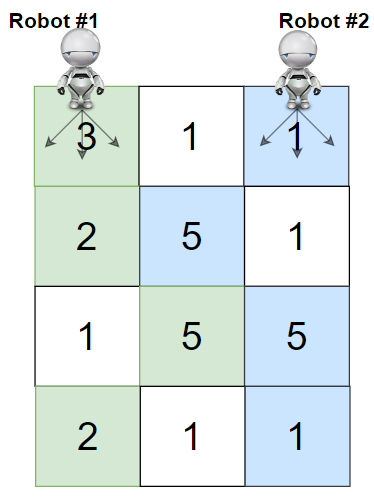
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/05/30/sample_1_1802.png)

**输入：** grid = [[3,1,1],[2,5,1],[1,5,5],[2,1,1]]
**输出：** 24
**解释：** 机器人 1 和机器人 2 的路径在上图中分别用绿色和蓝色表示。
机器人 1 摘的樱桃数目为 (3 + 2 + 5 + 2) = 12 。
机器人 2 摘的樱桃数目为 (1 + 5 + 5 + 1) = 12 。
樱桃总数为： 12 + 12 = 24 。

示例 2：

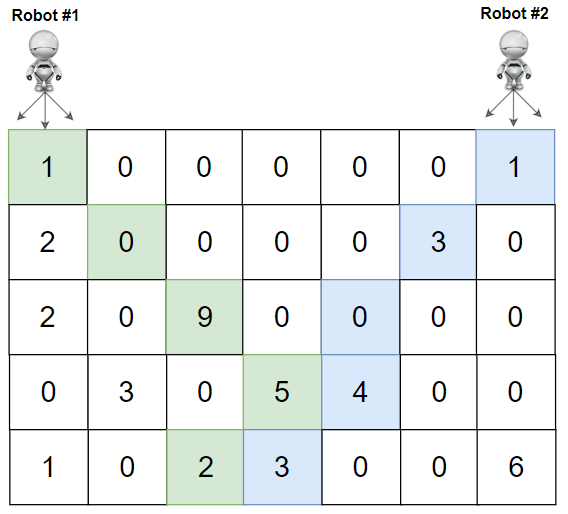
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/05/30/sample_2_1802.png)

**输入：** grid = [[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0,0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]]
**输出：** 28
**解释：** 机器人 1 和机器人 2 的路径在上图中分别用绿色和蓝色表示。
机器人 1 摘的樱桃数目为 (1 + 9 + 5 + 2) = 17 。
机器人 2 摘的樱桃数目为 (1 + 3 + 4 + 3) = 11 。
樱桃总数为： 17 + 11 = 28 。

示例 3：

**输入：** grid = [[1,0,0,3],[0,0,0,3],[0,0,3,3],[9,0,3,3]]
**输出：** 22

示例 4：

**输入：** grid = [[1,1],[1,1]]
**输出：** 4

提示：

rows == grid.length
cols == grid[i].length
2 <= rows, cols <= 70
0 <= grid[i][j] <= 100

方法一：动态规划

思路与算法

设矩阵的长度为 m，宽度为 n，我们用 f[i][j_1][j_2] 表示当第一个机器人从 (0, 0) 走到 (i, j_1)，第二个机器人从 (0, n-1) 走到 (i, j_2)，最多能收集的樱桃数目。

在进行状态转移时，我们可以枚举这两个机器人在第 i-1 行的位置 dj}_1 和 dj}_2，它们满足；

\begin{aligned}
0 \leq \textit{dj}_1 < n 且 \textit{dj}_1 - j_1 \in [-1, 0, 1] \
0 \leq \textit{dj}_2 < n 且 \textit{dj}_2 - j_2 \in [-1, 0, 1]
\end{aligned}

也就是说，我们只需要在 [j_1-1, j_1, j_1+1] 中枚举 dj}_1，并且需要判断其是否在 [0, n) 的范围内。对于 dj}_2 也是如此。因此我们可以写出如下的状态转移方程；

f[i][j_1][j_2] = \max(f[i-1][\textit{dj}_1][\textit{dj}_2] + \text{value}(i, j_1, j_2))

其中 value}(i, j_1, j_2) 表示两个机器人分别在 (i, j_1) 和 (i, j_2) 时可以收集的樱桃数目总和。根据题目描述，有：

\text{value}(i, j_1, j_2) =
\begin{cases}
\text{grid}[i][j_1] + \text{grid}[i][j_2] & 如果j_1 \neq j_2 \
\text{grid}[i][j_1] & 如果j_1 = j_2
\end{cases}

动态规划的边界条件为

f[i][0][n-1] = \text{grid}[0][0] + \text{grid}[0][n-1]

即两个机器人初始所在的位置。最终的答案即为所有 f[m-1][j_1][j_2] 中的最大值。

细节

动态规划一般有自顶向下和自底向上两种编写方式，其中自顶向下也被称为「记忆化搜索」。

如果我们用自顶向下的方式来编写代码，那么代码将会十分简洁，并且不需要考虑很多特殊情况和边界条件，这是因为「记忆化搜索」只会「搜索」可行的状态；
如果我们用自底向上的方式来编写代码，那么就需要考虑特殊情况和边界条件。例如在 i=0 时，除了 f[0][0][n-1] 之外的其余状态都是不合法的。对于这些状态，我们可以将其标记为 -1，并在状态转移时进行特殊判断。并且，我们可以发现在状态转移方程中，f[i][..][..] 只会从 f[i-1][..][..] 转移而来，因此我们可以使用两个二维数组代替三位数组，交替地进行状态转移，使空间复杂度得到优化。

下面的 C++ 和 Java 代码给出了自底向上 + 空间优化的参考；Python 代码给出了自顶向下的参考。

[sol1-C++]class Solution {
public:
    int cherryPickup(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        
        vector<vector<int>> f(n, vector<int>(n, -1)), g(n, vector<int>(n, -1));
        f[0][n - 1] = grid[0][0] + grid[0][n - 1];
        for (int i = 1; i < m; ++i) {
            for (int j1 = 0; j1 < n; ++j1) {
                for (int j2 = 0; j2 < n; ++j2) {
                    int best = -1;
                    for (int dj1 = j1 - 1; dj1 <= j1 + 1; ++dj1) {
                        for (int dj2 = j2 - 1; dj2 <= j2 + 1; ++dj2) {
                            if (dj1 >= 0 && dj1 < n && dj2 >= 0 && dj2 < n && f[dj1][dj2] != -1) {
                                best = max(best, f[dj1][dj2] + (j1 == j2 ? grid[i][j1] : grid[i][j1] + grid[i][j2]));
                            }
                        }
                    }
                    g[j1][j2] = best;
                }
            }
            swap(f, g);
        }

        int ans = 0;
        for (int j1 = 0; j1 < n; ++j1) {
            for (int j2 = 0; j2 < n; ++j2) {
                ans = max(ans, f[j1][j2]);
            }
        }
        return ans;
    }
};

[sol1-Java]class Solution {
    public int cherryPickup(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        
        int[][] f = new int[n][n];
        int[][] g = new int[n][n];
        for (int i = 0; i < n; i++) {
            Arrays.fill(f[i], -1);
            Arrays.fill(g[i], -1);
        }
        f[0][n - 1] = grid[0][0] + grid[0][n - 1];
        for (int i = 1; i < m; ++i) {
            for (int j1 = 0; j1 < n; ++j1) {
                for (int j2 = 0; j2 < n; ++j2) {
                    int best = -1;
                    for (int dj1 = j1 - 1; dj1 <= j1 + 1; ++dj1) {
                        for (int dj2 = j2 - 1; dj2 <= j2 + 1; ++dj2) {
                            if (dj1 >= 0 && dj1 < n && dj2 >= 0 && dj2 < n && f[dj1][dj2] != -1) {
                                best = Math.max(best, f[dj1][dj2] + (j1 == j2 ? grid[i][j1] : grid[i][j1] + grid[i][j2]));
                            }
                        }
                    }
                    g[j1][j2] = best;
                }
            }
            int[][] temp = f;
            f = g;
            g = temp;
        }

        int ans = 0;
        for (int j1 = 0; j1 < n; ++j1) {
            for (int j2 = 0; j2 < n; ++j2) {
                ans = Math.max(ans, f[j1][j2]);
            }
        }
        return ans;

    }
}

[sol1-Python3]class Solution:
    def cherryPickup(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])

        def getValue(i, j1, j2):
            return grid[i][j1] + grid[i][j2] if j1 != j2 else grid[i][j1]

        @lru_cache(None)
        def dfs(i, j1, j2):
            if i == m - 1:
                return getValue(i, j1, j2)
            
            best = 0
            for dj1 in [j1 - 1, j1, j1 + 1]:
                for dj2 in [j2 - 1, j2, j2 + 1]:
                    if 0 <= dj1 < n and 0 <= dj2 < n:
                        best = max(best, dfs(i + 1, dj1, dj2))

            return best + getValue(i, j1, j2)
        
        return dfs(0, 0, n - 1)

复杂度分析

时间复杂度：O(mn^2)。动态规划中的状态有 mn^2 个，对于每个状态，我们会从最多 3*3=9 个前置状态中选择一个进行转移。
空间复杂度：O(mn^2) 或 O(n^2)，取决于是否使用了空间优化。