1466-重新规划路线

n 座城市，从 0 到 n-1 编号，其间共有 n-1
条路线。因此，要想在两座不同城市之间旅行只有唯一一条路线可供选择（路线网形成一颗树）。去年，交通运输部决定重新规划路线，以改变交通拥堵的状况。

路线用 connections 表示，其中 connections[i] = [a, b] 表示从城市 a 到 b 的一条有向路线。

今年，城市 0 将会举办一场大型比赛，很多游客都想前往城市 0 。

请你帮助重新规划路线方向，使每个城市都可以访问城市 0 。返回需要变更方向的最小路线数。

题目数据保证每个城市在重新规划路线方向后都能到达城市 0 。

示例 1：

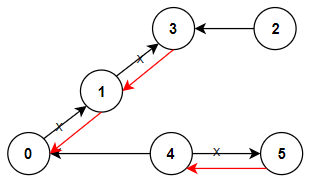
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/05/30/sample_1_1819.png)

**输入：** n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
**输出：** 3
**解释：** 更改以红色显示的路线的方向，使每个城市都可以到达城市 0 。

示例 2：

![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/05/30/sample_2_1819.png)

**输入：** n = 5, connections = [[1,0],[1,2],[3,2],[3,4]]
**输出：** 2
**解释：** 更改以红色显示的路线的方向，使每个城市都可以到达城市 0 。

示例 3：

**输入：** n = 3, connections = [[1,0],[2,0]]
**输出：** 0

提示：

2 <= n <= 5 * 10^4
connections.length == n-1
connections[i].length == 2
0 <= connections[i][0], connections[i][1] <= n-1
connections[i][0] != connections[i][1]

解题思路

此处撰写解题思路
结题思路都在代码提示里了,本题的解法里,从始至终都是有向图的思维,没有其他方法说的要把它当无向图的这种替代过程
既然是树形结构,那么,所有的点都是连接在一起的,就可以构建图

大体的思路就是先构建有向图,然后深度优先的方式从城市0的方向往外走的,因为整个结构是树(哪怕是多叉树,也不会有环的存在),因此从任意一个城市到达另一个城市,经过的城市是唯一的在深度遍历的过程中,如果发现方向是相反的,
说明是绕不过去的,只能修改方向,访问到的城市,由变量 boolean[] visited 记录,这个变量的状态值跟方向是无关的,访问到就到了,没有到就没有到

代码

/**
既然是树形结构,那么,所有的点都是连接在一起的,就可以构建图
根据题意,这是一个树形结构的有向无环图,如果不是树形的,比如题目变成了修路且无向的话,并查集就合适了,因为可能存在一个孤立的城市,跟任何城市可能都没关系
另外,这个解法是建立在树的结构这个约束条件下的,如果是真正的图的话,就不正确了,因为存在这么一种情况,所有节点其实都可以到达城市0,但是在深度遍历的过程中,
有可能某个路径是反方向的,此时计算的结果不会是0,但真正正确的答案是0
相当于整个算法的思维是降维的,用图来解决树的问题
 */
class Solution {
  private int count; // 变更方向的路线数

    public int minReorder(int n, int[][] connections) {
        // 构建有向图
        List<List<Integer>> graph = buildGraph(n, connections); 
        // 记录节点的访问状态
        boolean[] visited = new boolean[n]; 
         // 从节点0开始深度优先搜索
        dfs(graph, visited, 0);
         // 返回变更方向的路线数
        return count;
    }

    private void dfs(List<List<Integer>> graph, boolean[] visited, int city) {
        // 标记当前节点为已访问
        visited[city] = true; 
        for (int neighbor : graph.get(city)) {
            // 如果邻居节点未被访问
            if (!visited[Math.abs(neighbor)]) { 
                // 这里就体现出来有向的特性了,我们这个def方法,是从城市0的方向往外走的,因为整个结构是树(哪怕是多叉树,也不会有环的存在),因此从任意一个城市到达另一个城市,经过的城市是唯一的
                // ,如果neighbor>0,就说过没办法绕过其他城市抵达目标城市,必须要改路,因此count++
                if (neighbor > 0) {
                    // 需要变更方向的路线数增加
                    count++; 
                }
                // 继续深度优先搜索邻居节点
                dfs(graph, visited, Math.abs(neighbor)); 
            }
        }
    }

    /**
    n 是顶点的个数,connections用于创建邻接表
     */
    private List<List<Integer>> buildGraph(int n, int[][] connections) {
        // 用邻接表表示有向图
        List<List<Integer>> graph = new ArrayList<>(); 
        for (int i = 0; i < n; i++) {
            // 初始化每个节点的邻居列表
            graph.add(new ArrayList<>()); 
        }
        for (int[] connection : connections) {
            int from = connection[0];
            int to = connection[1];
            // 添加正向路线
            graph.get(from).add(to); 
            // 这里有个取巧的地方,添加反向路线，使用负数表示
            graph.get(to).add(-from);
        }
        return graph;
    }
}