1477-找两个和为目标值且不重叠的子数组

给你一个整数数组 arr 和一个整数值 target 。

请你在 arr 中找 两个互不重叠的子数组 且它们的和都等于 target 。可能会有多种方案，请你返回满足要求的两个子数组长度和的
最小值 。

请返回满足要求的最小长度和，如果无法找到这样的两个子数组，请返回 -1 。

示例 1：

**输入：** arr = [3,2,2,4,3], target = 3
**输出：** 2
**解释：** 只有两个子数组和为 3 （[3] 和 [3]）。它们的长度和为 2 。

示例 2：

**输入：** arr = [7,3,4,7], target = 7
**输出：** 2
**解释：** 尽管我们有 3 个互不重叠的子数组和为 7 （[7], [3,4] 和 [7]），但我们会选择第一个和第三个子数组，因为它们的长度和 2 是最小值。

示例 3：

**输入：** arr = [4,3,2,6,2,3,4], target = 6
**输出：** -1
**解释：** 我们只有一个和为 6 的子数组。

示例 4：

**输入：** arr = [5,5,4,4,5], target = 3
**输出：** -1
**解释：** 我们无法找到和为 3 的子数组。

示例 5：

**输入：** arr = [3,1,1,1,5,1,2,1], target = 3
**输出：** 3
**解释：** 注意子数组 [1,2] 和 [2,1] 不能成为一个方案因为它们重叠了。

提示：

• 1 <= arr.length <= 10^5
• 1 <= arr[i] <= 1000
• 1 <= target <= 10^8

本题要解决两个问题：
1、寻找和为target的子数组
2、这样的子数组要找两个，且不重叠

先看第一个问题，如何寻找和为target的子数组。比较容易想到的方法就是前缀和。一般的，如果arr[0,i]的前缀和为presum，arr[0,j]的前缀和也为presum，那么arr[i+1,j]的和就等于0。更进一步，如果arr[0,j]的前缀和为presum+target，那么arr[i+1,j]的和就等于target。所以我们只需要遍历一次数组，计算每一个presum，同时判断presum-target在之前是否已经存在了（使用hash表记录下已经存在的presum），如果存在就说明找到一个满足条件的子数组。遍历完成就能找出所有满足条件的子数组。

本题由于限定了arr[i]是正整数，所以有更快的方法找到和为target的子数组，那就是双指针。我们用两个指针left、right分别指向子数组的首尾部，然后计算该子数组的和，如果大于target，说明数多了，我们++left收缩数组大小；如果小于target，说明数少了，我们++right扩大数组大小。当子数组的和刚好等于target时，我们找到一个满足条件的子数组。注意如果arr[i]可以取负数，那么此方法就不成立了，因为当arr[i]可以取负数时，扩大数组大小也能使和变小，这样就不具备单调性了。

实测在数据量较大的情况下，双指针会明显比hash表更快：

再看第二个问题，要如何找到两个最短的并且不重叠的子数组。最朴素的想法就是找到所有满足条件的子数组后，按照长度排序，然后贪心选择两个最短的。如果这两个子数组不重叠，那么我们就找到了最终答案。如果有重叠发生，就尝试换另外一个短的子数组。该思路理论上可行，不过要同时控制两个因素：两个子数组的长度和最短、两个子数组不重叠，实现起来比较繁琐。这里，我们重点考虑不重叠的问题，采用动态规划的思路，遍历所有可能的子数组和，找出里面和最小的。

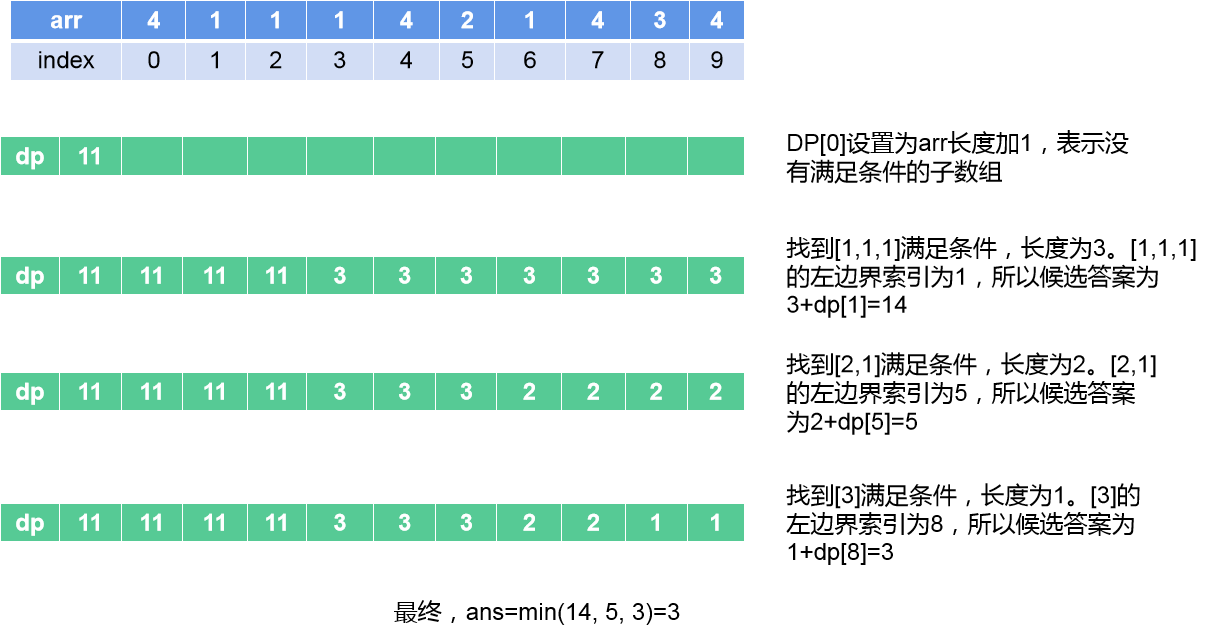
由于要确保子数组不重叠，我们很自然的想到将数组分为前后两部分，每一次当我们找到一个满足条件的子数组时，假设这个子数组处于后半部分，如果能够知道这个子数组前面最短的子数组是多少，那么这两个长度相加就构成了一个可选的答案。当遍历完所有的后半部分的子数组时，可选答案中和最小的就是最终的答案。来看一个例子，考察数组arr=[4,1,1,1,4,2,1,4,3,4]，target=3，令dp[i]表示子数组arr[0,i)里面满足条件的子数组的最短长度：

1、为方便边界处理，dp比arr长一个，dp[i+1]对应arr[i]，dp[0]初始化为一个比arr长度大的值，表示没有满足条件的子数组。在搜索过程中，如果没有找到一个满足条件的子数组，那么dp[i]保持不变，即dp[i]=dp[i-1]

2、首先找到子数组[1,1,1]，长度为3。该子数组右边界为index3，这意味着所有i大于3的dp[i]最大只能是3。即所有包含[1,1,1]的子数组，它的最短长度最大只能是3。另外，没有必要立即更新dp[4]~dp[10]，只需要更新dp[4]，并记录下这个最小值就可以了。于此同时，因为[1,1,1]的左边界为index1，我们得到了一个候选答案3+dp[1]=14。

3、然后找到子数组[2,1]，长度为2，比前一个子数组更短。该子数组右边界为index6，这意味着所有i大于6的dp[i]最大只能是2。因为[2,1]的左边界为index5，我们得到了一个候选答案2+dp[5]=5。

4、最后找到子数组[3]，长度为1。该子数组右边界为index8，这意味着所有i大于8的dp[i]最大只能是1。因为[3]的左边界为index8，我们得到了一个候选答案1+dp[8]=3。

5、最终的答案在{14,5,3}之中产生，很明显应该选3。如果所有候选答案都大于数组的长度，说明没有找到两个不重合的子数组，那就应该返回-1。

class Solution {
public:
    int minSumOfLengths(vector<int>& arr, int target) {
        int size = arr.size(), left = 0, right, sum = 0, minSumOfLens = INT_MAX;
        vector<int> dp(size + 1, 0);
        dp[0] = size + 1;  // dp[i]表示区间[0,i)之间最短的和为target的子数组，先初始化为一个较大的数表示不存在。因为会做加法运算，不能初始化为INT_MAX

        for (right = 0; right < size; ++right) {
            sum += arr[right];

            while (sum > target) {
                sum -= arr[left++];
            }

            if (sum == target) {
                int len = right - left + 1;  // 区间[left,right]是一个和为target的子数组，该子数组长度为len
                minSumOfLens = min(minSumOfLens, len + dp[left]);  // 如果有解，我们遍历了所有的第二个子数组，同时加上它前面长度最短的第一个子数组就是答案
                dp[right + 1] = min(dp[right], len);  // 更新dp，取长度更小的一个
            }
            else {
                dp[right + 1] = dp[right];  // 不是一个和为target的子数组，dp[i]保持不变
            }
        }

        return minSumOfLens > size ? -1 : minSumOfLens;  // 大于size说明没有找到两个不重叠的子数组
    }
};