1478-安排邮筒

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:31 2023-09-13 16:06:31 Updated    

给你一个房屋数组houses 和一个整数 k ，其中 houses[i] 是第 i 栋房子在一条街上的位置，现需要在这条街上安排 k
个邮筒。

请你返回每栋房子与离它最近的邮筒之间的距离的 最小 总和。

答案保证在 32 位有符号整数范围以内。

示例 1：

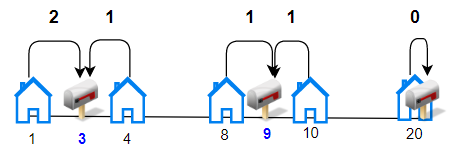
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/06/13/sample_11_1816.png)

**输入：** houses = [1,4,8,10,20], k = 3
**输出：** 5
**解释：** 将邮筒分别安放在位置 3， 9 和 20 处。
每个房子到最近邮筒的距离和为 |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5 。

示例 2：

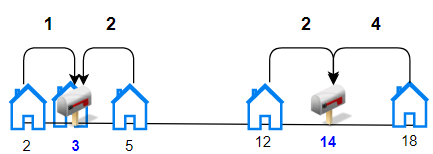
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/06/13/sample_2_1816.png)

**输入：** houses = [2,3,5,12,18], k = 2
**输出：** 9
**解释：** 将邮筒分别安放在位置 3 和 14 处。
每个房子到最近邮筒距离和为 |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9 。

示例 3：

**输入：** houses = [7,4,6,1], k = 1
**输出：** 8

示例 4：

**输入：** houses = [3,6,14,10], k = 4
**输出：** 0

提示：

  • n == houses.length
  • 1 <= n <= 100
  • 1 <= houses[i] <= 10^4
  • 1 <= k <= n
  • 数组 houses 中的整数互不相同。

方法一：动态规划

思路与算法

我们称「一个邮筒负责一栋房子」，当且仅当该邮筒是距离该房子最近的邮筒。那么对于任意一个邮筒，它负责的房子的集合在数轴上是连续的。因此，我们可以将数组 houses 进行排序，这样就可以方便地给这些房子安排邮筒了。

我们用 f[i][j] 表示给前 i 栋房子（从 0 开始编号）安排 j 个邮筒（从 1 开始编号）的最小距离总和。在进行状态转移时，我们可以枚举第 j 个邮筒负责的房子的起始编号，从 i_0+1 开始，到 i 结束。这样我们就可以写出状态转移方程：

f[i][j] = \min(f[i_0][j-1] + \mathrm{cost}(i_0+1, i))

以及边界条件

f[i][1] = \mathrm{cost}(0, i)

其中 \mathrm{cost}(l, r) 表示给排好序的 houses}[l] 到 houses}[r] 的房子安排一个邮筒，可以得到的最小距离总和。那么如何计算 \mathrm{cost}(l, r) 呢？设想一下，如果在数轴上有若干个点组成了集合 \mathcal{X，我们需要找出一个目标点 x，使得 \mathcal{X 到 x 的距离和最小。那么我们应当选择 \mathcal{X 的中位数作为目标点，即 x = \mathrm{median}(\mathcal{X})。

这个结论是比较直观的：选择中位数作为目标点，使得 \mathcal{X 中小于 x 的点数恰好等于 \mathcal{X 中大于 x 的点数，达到了一个平衡。如果我们选择的目标点小于中位数，那么 \mathcal{X 中大于 x 的点数要多一些，我们将目标点向中位数的方向（向右）移动，距离和就会减小。同理可得如果我们选择的目标点大于中位数，那么将目标点向左移动，距离和就会减小。因此选择中位数作为目标点是最优的。

如果读者希望得到具体的证明，可以参考下面「正确性证明」的部分。

当 x = \mathrm{median}(\mathcal{X}) 时，\mathrm{cost}(l, r) 的计算也并不复杂：由于 houses}[l .. r] 的中位数与 houses}[l+1 .. r-1] 的中位数是相同的，而 houses}[l] 和 houses}[r] 与中位数的距离和恰好等于 houses}[r] - \textit{houses}[l]。因此，我们可以使用递推的方法计算 \mathrm{cost}(l, r)，即：

\mathrm{cost}(l, r) = \mathrm{cost}(l+1, r-1) + (\textit{houses}[r] - \textit{houses}[l])

我们可以使用 O(n^2) 的时间预处理出所有的 \mathrm{cost}(l, r)，其中 n 是数组 houses 的长度。这样一来，我们就在动态规划的部分快速地进行状态转移了。

最终的答案即为 f[n-1][k]。

细节

在动态规划中，有一些状态是无意义的，我们可以不必去计算。对于 f[i][j]，显然需要满足 j \leq i+1，也就是邮筒的数量不会超过房子的数量。对于这些状态，我们可以在对数组 f 进行初始化的时候，将它们赋值成一个很大的数（因为状态转移方程中为 \min），并且在动态规划的过程中不去枚举这些状态，这样这些无意义的状态既不会被计算，也不会参与状态转移。

正确性证明

设数组 a 包含 n 个元素 a[1], a[2], \cdots, a[n]，且它们互不相同。下证当 x = \mathrm{median}(a) 时，

\sum_{i=1}^n |a[i] - x|

取到最小值，且最小值为

\sum_{i=1}^{\lfloor n/2 \rfloor} (a[n+1-i] - a[i])

证明：将数组 a 进行升序排序，并补充 a[0] = -\infty 以及 a[n+1] = \infty。记

f(x) = \sum_{i=1}^n |a[i] - x|

求导可得

f’(x) = \sum_{i=1}^n \mathbb{I}(a[i])

其中 \mathbb{I}(a) 为示性函数

\mathbb{I}(a) = \begin{cases}
1, & x > a[i] \
0, & x = a[i] \
-1, & x < a[i]
\end{cases}

由于 a[0] 到 a[n+1] 有序，那么存在 i_0 \in [0, n+1) 使得 a[i_0] \leq x < a[i_0+1]。

  • 如果 a[i_0] < x < a[i_0+1]，那么

    f’(x) = \sum_{i=1}^{i_0} 1 + \sum_{i=i_0+1}^n (-1) = 2i_0 - n

  • 如果 x = a[i_0]，那么 f(x) 在该点连续但不可导。

要想找到 f(x) 的最小值，我们只需要关注 f’(x) 的正负性。由

f’(x) = 2i_0 - n < 0

可得 i_0 \leq \lfloor (n-1)/2 \rfloor，即当 x < a[\lfloor (n+1)/2 \rfloor] 时，f’(x) < 0，f(x) 单调减。同理可得，当 i_0 \geq \lceil (n+1)/2 \rceil，即当 x > a[\lceil (n+1)/2 \rceil] 时，f’(x) > 0，f(x) 单调增。也就是说：

  • 当 n 为奇数时，\lfloor (n+1)/2 \rfloor = \lceil (n+1)/2 \rceil = (n+1)/2，f(x) 在 x = a[(n+1)/2] 处取到最小值，对应了数组 a 的中位数；

  • 当 n 为偶数时，\lfloor (n+1)/2 \rfloor = n/2，\lceil (n+1)/2 \rceil = n/2+1，f(x) 在 x \in [a[n/2], a[n/2+1]] 处取到最小值，而数组 a 的中位数 1/2 \cdot (a[n/2] + a[n/2+1]) 就包含在该区间中。

因此我们可以取 x = \mathrm{median}(a)。此时，对应的最小值为：

\begin{aligned}
\sum_{i=1}^n |a[i] - x| &= \sum_{a_i < x} (x-a[i]) + \sum_{a_i > x} (a[i]-x) \
&= \sum_{i=1}^{\lfloor n/2 \rfloor} (x-a[i]) + \sum_{i=\lceil n/2 \rceil + 1}^{n} (a[i]-x) \
&= \sum_{i=1}^{\lfloor n/2 \rfloor} (x-a[i]) + \sum_{j=1}^{\lfloor n/2 \rfloor} (a[n+1-j]-x) \
&= \sum_{i=1}^{\lfloor n/2 \rfloor} (a[n+1-i] - a[i])
\end{aligned}

其中使用了代换 j=n+1-i 以及一个简单的结论 \lfloor n/2 \rfloor + \lceil n/2 \rceil = n。

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int minDistance(vector<int>& houses, int k) {
        int n = houses.size();
        sort(houses.begin(), houses.end());

        vector<vector<int>> medsum(n, vector<int>(n));
        for (int i = n - 2; i >= 0; --i) {
            for (int j = i + 1; j < n; ++j) {
                medsum[i][j] = medsum[i + 1][j - 1] + houses[j] - houses[i];
            }
        }

        vector<vector<int>> f(n, vector<int>(k + 1, INT_MAX / 2));
        for (int i = 0; i < n; ++i) {
            f[i][1] = medsum[0][i];
            for (int j = 2; j <= k && j <= i + 1; ++j) {
                for (int i0 = 0; i0 < i; ++i0) {
                    f[i][j] = min(f[i][j], f[i0][j - 1] + medsum[i0 + 1][i]);
                }
            }
        }

        return f[n - 1][k];
    }
};
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public int minDistance(int[] houses, int k) {
        int n = houses.length;
        Arrays.sort(houses);

        int[][] medsum = new int[n][n];
        for (int i = n - 2; i >= 0; --i) {
            for (int j = i + 1; j < n; ++j) {
                medsum[i][j] = medsum[i + 1][j - 1] + houses[j] - houses[i];
            }
        }

        int[][] f = new int[n][k + 1];
        for (int i = 0; i < n; ++i) {
            Arrays.fill(f[i], Integer.MAX_VALUE / 2);
        }
        for (int i = 0; i < n; ++i) {
            f[i][1] = medsum[0][i];
            for (int j = 2; j <= k && j <= i + 1; ++j) {
                for (int i0 = 0; i0 < i; ++i0) {
                    f[i][j] = Math.min(f[i][j], f[i0][j - 1] + medsum[i0 + 1][i]);
                }
            }
        }

        return f[n - 1][k];
    }
}
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution:
    def minDistance(self, houses: List[int], k: int) -> int:
        n = len(houses)
        houses.sort()

        medsum = [[0] * n for _ in range(n)]
        for i in range(n - 2, -1, -1):
            for j in range(i + 1, n):
                medsum[i][j] = medsum[i + 1][j - 1] + houses[j] - houses[i]
        
        BIG = 10**9
        f = [[BIG] * (k + 1) for _ in range(n)]
        for i in range(n):
            f[i][1] = medsum[0][i]
            for j in range(2, min(k, i + 1) + 1):
                for i0 in range(i):
                    if f[i0][j - 1] != BIG:
                        f[i][j] = min(f[i][j], f[i0][j - 1] + medsum[i0 + 1][i])
        
        return f[n - 1][k]

复杂度分析

  • 时间复杂度：O(n^2k)，其中 n 是数组 houses 的长度。在预处理部分，需要的时间为 O(n^2)；在动态规划部分，我们需要 O(nk) 的时间枚举每个状态 f[i][j]，并使用 O(n) 的时间枚举 i_0 进行状态转移，相乘即可得到总时间复杂度。

  • 空间复杂度：O(n^2 + nk)，即为存储 \mathrm{cost 以及动态规划的状态需要的空间。

 Comments
On this page
1478-安排邮筒