1483-树节点的第 K 个祖先

给你一棵树，树上有 n 个节点，按从 0 到 n-1 编号。树以父节点数组的形式给出，其中 parent[i] 是节点 i
的父节点。树的根节点是编号为 0 的节点。

树节点的第 _k _个祖先节点是从该节点到根节点路径上的第 k 个节点。

实现 TreeAncestor 类：

• TreeAncestor（int n， int[] parent） 对树和父数组中的节点数初始化对象。
• getKthAncestor``(int node, int k) 返回节点 node 的第 k 个祖先节点。如果不存在这样的祖先节点，返回 -1 。

示例 1：

![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/06/14/1528_ex1.png)

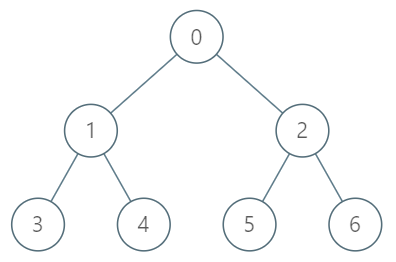
**输入：**
["TreeAncestor","getKthAncestor","getKthAncestor","getKthAncestor"]
[[7,[-1,0,0,1,1,2,2]],[3,1],[5,2],[6,3]]

**输出：**
[null,1,0,-1]

**解释：**
TreeAncestor treeAncestor = new TreeAncestor(7, [-1, 0, 0, 1, 1, 2, 2]);

treeAncestor.getKthAncestor(3, 1);  // 返回 1 ，它是 3 的父节点
treeAncestor.getKthAncestor(5, 2);  // 返回 0 ，它是 5 的祖父节点
treeAncestor.getKthAncestor(6, 3);  // 返回 -1 因为不存在满足要求的祖先节点

提示：

• 1 <= k <= n <= 5 * 104
• parent[0] == -1 表示编号为 0 的节点是根节点。
• 对于所有的 0 < i < n ，0 <= parent[i] < n 总成立
• 0 <= node < n
• 至多查询 5 * 104 次

方法一：倍增

思路

倍增的思路类似于动态规划，定义 ancestors}[i][j] 表示节点 i 的第 2^j 个祖先。此题中，树最多有 50000 个节点，因此 ancestors 的第二维度的最大值可以设为 16。根据定义，ancestors}[i][0] = \textit{parent}[i]。状态转移方程是 ancestors}[i][j] = \textit{ancestors}[\textit{ancestors}[i][j - 1]][j - 1]，即当前节点的第 2^j 个祖先，是他的第 2^{j-1 个祖先的第 2^{j-1 个祖先。当第 2^j 个祖先不存在时，记为 -1。

查询时，需要将 k 的二进制表示从最低位到最高位依次进行判断，如果第 j 位为 1，则节点 node 需要进行转移到 ancestors}[\textit{node}][j]，表示 node 向祖先方向移动了 2^j 次。直至遍历完 k 所有位或者 node 变为 -1。

代码

[sol1-Python3]

class TreeAncestor:

    def __init__(self, n: int, parent: List[int]):
        self.log = 16
        self.ancestors = [[-1] * self.log for _ in range(n)]
        for i in range(n):
            self.ancestors[i][0] = parent[i]
        for j in range(1, self.log):
            for i in range(n):
                if self.ancestors[i][j - 1] != -1:
                    self.ancestors[i][j] = self.ancestors[self.ancestors[i][j - 1]][j - 1]   

    def getKthAncestor(self, node: int, k: int) -> int:
        for j in range(self.log):
            if (k>>j) & 1: 
                node = self.ancestors[node][j]
                if node == -1:
                    return -1
        return node

[sol1-C++]

class TreeAncestor {
public:
    constexpr static int Log = 16;
    vector<vector<int>> ancestors;

    TreeAncestor(int n, vector<int>& parent) {
        ancestors = vector<vector<int>>(n, vector<int>(Log, -1));
        for (int i = 0; i < n; i++) {
            ancestors[i][0] = parent[i];
        }
        for (int j = 1; j < Log; j++) {
            for (int i = 0; i < n; i++) {
                if (ancestors[i][j - 1] != -1) {
                    ancestors[i][j] = ancestors[ancestors[i][j - 1]][j - 1];
                }
            }
        }            
    }

    int getKthAncestor(int node, int k) {
        for (int j = 0; j < Log; j++) {
            if ((k >> j) & 1) {
                node = ancestors[node][j];
                if (node == -1) {
                    return -1;
                }
            }
        }
        return node;
    }
};

[sol1-Java]

class TreeAncestor {
    static final int LOG = 16;
    int[][] ancestors;

    public TreeAncestor(int n, int[] parent) {
        ancestors = new int[n][LOG];
        for (int i = 0; i < n; i++) {
            Arrays.fill(ancestors[i], -1);
        }
        for (int i = 0; i < n; i++) {
            ancestors[i][0] = parent[i];
        }
        for (int j = 1; j < LOG; j++) {
            for (int i = 0; i < n; i++) {
                if (ancestors[i][j - 1] != -1) {
                    ancestors[i][j] = ancestors[ancestors[i][j - 1]][j - 1];
                }
            }
        }            
    }

    public int getKthAncestor(int node, int k) {
        for (int j = 0; j < LOG; j++) {
            if (((k >> j) & 1) != 0) {
                node = ancestors[node][j];
                if (node == -1) {
                    return -1;
                }
            }
        }
        return node;
    }
}

[sol1-C#]

public class TreeAncestor {
    const int LOG = 16;
    int[][] ancestors;

    public TreeAncestor(int n, int[] parent) {
        ancestors = new int[n][];
        for (int i = 0; i < n; i++) {
            ancestors[i] = new int[LOG];
            Array.Fill(ancestors[i], -1);
        }
        for (int i = 0; i < n; i++) {
            ancestors[i][0] = parent[i];
        }
        for (int j = 1; j < LOG; j++) {
            for (int i = 0; i < n; i++) {
                if (ancestors[i][j - 1] != -1) {
                    ancestors[i][j] = ancestors[ancestors[i][j - 1]][j - 1];
                }
            }
        }            
    }

    public int GetKthAncestor(int node, int k) {
        for (int j = 0; j < LOG; j++) {
            if (((k >> j) & 1) != 0) {
                node = ancestors[node][j];
                if (node == -1) {
                    return -1;
                }
            }
        }
        return node;
    }
}

[sol1-Golang]

const kLog = 16

type TreeAncestor struct {
    ancestors [][]int
}

func Constructor(n int, parent []int) TreeAncestor {
    var this TreeAncestor
    this.ancestors = make([][]int, n)
    for i := 0; i < n; i++ {
        this.ancestors[i] = make([]int, kLog)
        for j := 0; j < kLog; j++ {
            this.ancestors[i][j] = -1
        }
        this.ancestors[i][0] = parent[i]
    }
    for j := 1; j < kLog; j++ {
        for i := 0; i < n; i++ {
            if this.ancestors[i][j - 1] != -1 {
                this.ancestors[i][j] = this.ancestors[this.ancestors[i][j - 1]][j - 1]
            }
        }
    }
    return this
}

func (this *TreeAncestor) GetKthAncestor(node int, k int) int {
    for j := 0; j < kLog; j++ {
        if (k >> j) & 1 != 0 {
            node = this.ancestors[node][j]
            if node == -1 {
                return -1
            }
        }
    }
    return node
}

[sol1-C]

const int LOG = 16;

typedef struct {
    int **ancestors;
    int n;
} TreeAncestor;

TreeAncestor* treeAncestorCreate(int n, int* parent, int parentSize) {
    TreeAncestor *obj = (TreeAncestor *)malloc(sizeof(TreeAncestor));
    obj->ancestors = (int **)malloc(sizeof(int *) * n);
    for (int i = 0; i < n; i++) {
        obj->ancestors[i] = (int *)malloc(sizeof(int) * LOG);
        memset(obj->ancestors[i], 0xff, sizeof(int) * LOG);
    }
    for (int i = 0; i < n; i++) {
        obj->ancestors[i][0] = parent[i];
    }
    for (int j = 1; j < LOG; j++) {
        for (int i = 0; i < n; i++) {
            if (obj->ancestors[i][j - 1] != -1) {
                obj->ancestors[i][j] = obj->ancestors[obj->ancestors[i][j - 1]][j - 1];
            }
        }
    }    
    return obj;  
}

int treeAncestorGetKthAncestor(TreeAncestor* obj, int node, int k) {
    for (int j = 0; j < LOG; j++) {
        if ((k >> j) & 1) {
            node = obj->ancestors[node][j];
            if (node == -1) {
                return -1;
            }
        }
    }
    return node;
}

void treeAncestorFree(TreeAncestor* obj) {
    for (int i = 0; i < obj->n; i++) {
        free(obj->ancestors[i]);
    }
    free(obj->ancestors);
    free(obj);
}

[sol1-JavaScript]

const LOG = 16;
var TreeAncestor = function(n, parent) {
    ancestors = new Array(n).fill(0).map(() => new Array(LOG).fill(-1));
    for (let i = 0; i < n; i++) {
        ancestors[i][0] = parent[i];
    }
    for (let j = 1; j < LOG; j++) {
        for (let i = 0; i < n; i++) {
            if (ancestors[i][j - 1] !== -1) {
                ancestors[i][j] = ancestors[ancestors[i][j - 1]][j - 1];
            }
        }
    }                 
}

TreeAncestor.prototype.getKthAncestor = function(node, k) {
    for (let j = 0; j < LOG; j++) {
        if (((k >> j) & 1) !== 0) {
            node = ancestors[node][j];
            if (node === -1) {
                return -1;
            }
        }
    }
    return node;
};  

复杂度分析

• 时间复杂度：初始化的时间复杂度是 O(n\times\log{n})，单次查询的时间复杂度是 O(\log{n})。

• 空间复杂度：初始化的空间复杂度是 O(n\times\log{n})，单次查询的空间复杂度是 O(1)。