1503-所有蚂蚁掉下来前的最后一刻
有一块木板,长度为 n 个 单位 。一些蚂蚁在木板上移动,每只蚂蚁都以 每秒一个单位 的速度移动。其中,一部分蚂蚁向 左
移动,其他蚂蚁向 右 移动。
当两只向 不同 方向移动的蚂蚁在某个点相遇时,它们会同时改变移动方向并继续移动。假设更改方向不会花费任何额外时间。
而当蚂蚁在某一时刻 t 到达木板的一端时,它立即从木板上掉下来。
给你一个整数 n 和两个整数数组 left 以及 right 。两个数组分别标识向左或者向右移动的蚂蚁在 t = 0
时的位置。请你返回最后一只蚂蚁从木板上掉下来的时刻。
示例 1:
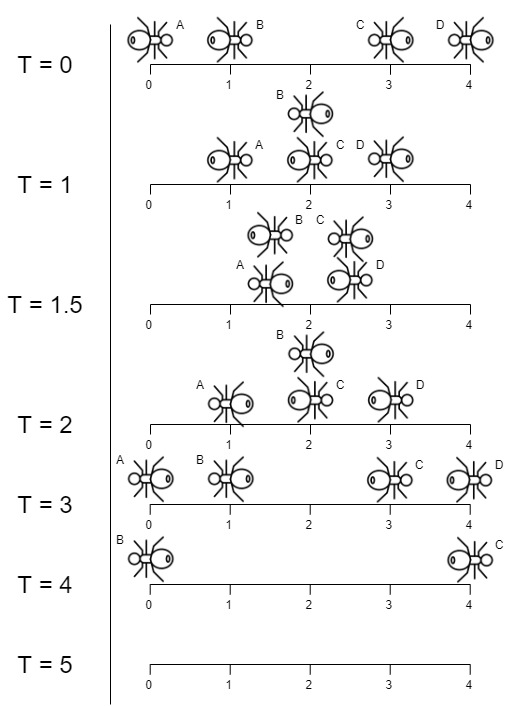
**输入:** n = 4, left = [4,3], right = [0,1]
**输出:** 4
**解释:** 如上图所示:
-下标 0 处的蚂蚁命名为 A 并向右移动。
-下标 1 处的蚂蚁命名为 B 并向右移动。
-下标 3 处的蚂蚁命名为 C 并向左移动。
-下标 4 处的蚂蚁命名为 D 并向左移动。
请注意,蚂蚁在木板上的最后时刻是 t = 4 秒,之后蚂蚁立即从木板上掉下来。(也就是说在 t = 4.0000000001 时,木板上没有蚂蚁)。
示例 2:

**输入:** n = 7, left = [], right = [0,1,2,3,4,5,6,7]
**输出:** 7
**解释:** 所有蚂蚁都向右移动,下标为 0 的蚂蚁需要 7 秒才能从木板上掉落。
示例 3:

**输入:** n = 7, left = [0,1,2,3,4,5,6,7], right = []
**输出:** 7
**解释:** 所有蚂蚁都向左移动,下标为 7 的蚂蚁需要 7 秒才能从木板上掉落。
提示:
1 <= n <= 10^40 <= left.length <= n + 10 <= left[i] <= n0 <= right.length <= n + 10 <= right[i] <= n1 <= left.length + right.length <= n + 1left和right中的所有值都是唯一的,并且每个值 只能出现在二者之一 中。
方法一:模拟
这道题最容易让人迷惑的地方在于「当两只向不同方向移动的蚂蚁在某个点相遇时,它们会同时改变移动方向并继续移动」。按照常规思路,需要对每只蚂蚁分别计算每个时刻所在的位置,如果考虑到改变移动方向,情况会非常复杂。
注意到题目要求的是最后一只蚂蚁从木板上掉下来的时刻,所以并不需要区分每只蚂蚁。注意到题目中的信息,由于改变移动方向不花费额外时间,而且改变移动方向后的移动速度不变,因此,两只相遇的蚂蚁同时改变移动方向之后的情形等价于两只蚂蚁都不改变移动方向,继续按照原来的方向和速度移动,这样问题就简化成根据每只蚂蚁的初始位置和移动方向得到最后一只蚂蚁到达木板边界的时刻。
假设一只蚂蚁在位置 p。如果这只蚂蚁向左移动,则它到达木板边界需要的时间是 p。如果这只蚂蚁向右移动,则它到达木板边界需要的时间是 n-p。
遍历数组 left 和 right,根据每只蚂蚁的初始位置和移动方向得到每只蚂蚁到达木板边界需要的时间,其中的最大值即为最后一只蚂蚁到达木板边界的时刻,也是最后一只蚂蚁从木板上掉下来的时刻。
1 | class Solution { |
1 | public class Solution |
1 | class Solution { |
1 | class Solution: |
复杂度分析
时间复杂度:O(n)。需要遍历 left 和 right 两个数组,因此时间复杂度与两个数组的长度之和呈线性关系,又由于两个数组的长度之和最大为 n+1,因此时间复杂度是 O(n)。
空间复杂度:O(1)。