1514-概率最大的路径

给你一个由 n 个节点（下标从 0 开始）组成的无向加权图，该图由一个描述边的列表组成，其中 edges[i] = [a, b] 表示连接节点 a
和 b 的一条无向边，且该边遍历成功的概率为 succProb[i] 。

指定两个节点分别作为起点 start 和终点 end ，请你找出从起点到终点成功概率最大的路径，并返回其成功概率。

如果不存在从 start 到 end 的路径，请 返回 0 。只要答案与标准答案的误差不超过 1e-5 ，就会被视作正确答案。

示例 1：

![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/07/12/1558_ex1.png)

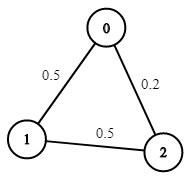
**输入：** n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
**输出：** 0.25000
**解释：** 从起点到终点有两条路径，其中一条的成功概率为 0.2 ，而另一条为 0.5 * 0.5 = 0.25

示例 2：

![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/07/12/1558_ex2.png)

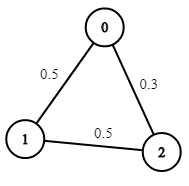
**输入：** n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2
**输出：** 0.30000

示例 3：

![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/07/12/1558_ex3.png)

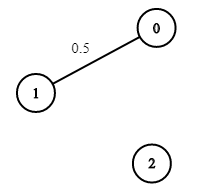
**输入：** n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
**输出：** 0.00000
**解释：** 节点 0 和 节点 2 之间不存在路径

提示：

• 2 <= n <= 10^4
• 0 <= start, end < n
• start != end
• 0 <= a, b < n
• a != b
• 0 <= succProb.length == edges.length <= 2*10^4
• 0 <= succProb[i] <= 1
• 每两个节点之间最多有一条边

写在前面

本题需要用到单源最短路径算法 Dijkstra，现在让我们回顾该算法，其主要思想是贪心，具体地说：

将所有节点分成两类：已确定从起点到当前点的最短路长度的节点，以及未确定从起点到当前点的最短路长度的节点（下面简称「未确定节点」和「已确定节点」）。

每次从「未确定节点」中取一个与起点距离最短的点，将它归类为「已确定节点」，并用它「更新」从起点到其他所有「未确定节点」的距离。直到所有点都被归类为「已确定节点」。

用节点 A「更新」节点 B 的意思是，用起点到节点 A 的最短路长度加上从节点 A 到节点 B 的边的长度，去比较起点到节点 B 的最短路长度，如果前者小于后者，就用前者更新后者。这种操作也被叫做「松弛」。

这里暗含的信息是：每次选择「未确定节点」时，起点到它的最短路径的长度可以被确定。

可以这样理解，因为我们已经用了每一个「已确定节点」更新过了当前节点，无需再次更新（因为一个点不能多次到达）。而当前节点已经是所有「未确定节点」中与起点距离最短的点，不可能被其它「未确定节点」更新。所以当前节点可以被归类为「已确定节点」。

给定的图必须是正边权图，否则「未确定节点」有可能更新当前节点，这也是 Dijkstra 不能处理负权图的原因。

方法一：Dijkstra 算法

思路及算法

本题是一种变种的最短路径问题。特殊点在于，我们选取的每一条边对答案的贡献是以相乘的形式，而不是相加的形式。

为什么当前图能使用 Dijkstra 算法呢？因为该图的边权都是位于区间 [0,1] 的小数（概率），即沿着一条边移动无法让边权积增大，只会减小或不变。而我们要求的是最大边权积，这符合了 Dijkstra 算法的思想和要求。严谨的证明见「正确性证明」部分。

普通的 Dijkstra 算法是通过枚举来寻找「未确定节点」中与起点距离最近的点。在实际实现中，我们可以使用优先队列优化这一过程的时间复杂度。

代码

[sol1-C++]

class Solution {
public:
    double maxProbability(int n, vector<vector<int>>& edges, vector<double>& succProb, int start, int end) {
        vector<vector<pair<double, int>>> graph(n);
        for (int i = 0; i < edges.size(); i++) {
            auto& e = edges[i];
            graph[e[0]].emplace_back(succProb[i], e[1]);
            graph[e[1]].emplace_back(succProb[i], e[0]);
        }

        priority_queue<pair<double, int>> que;
        vector<double> prob(n, 0);

        que.emplace(1, start);
        prob[start] = 1;
        while (!que.empty()) {
            auto [pr, node] = que.top();
            que.pop();
            if (pr < prob[node]) {
                continue;
            }
            for (auto& [prNext, nodeNext] : graph[node]) {
                if (prob[nodeNext] < prob[node] * prNext) {
                    prob[nodeNext] = prob[node] * prNext;
                    que.emplace(prob[nodeNext], nodeNext);
                }
            }
        }
        return prob[end];
    }
};

[sol1-Java]

class Solution {
    public double maxProbability(int n, int[][] edges, double[] succProb, int start, int end) {
        List<List<Pair>> graph = new ArrayList<List<Pair>>();
        for (int i = 0; i < n; i++) {
            graph.add(new ArrayList<Pair>());
        }
        for (int i = 0; i < edges.length; i++) {
            int[] e = edges[i];
            graph.get(e[0]).add(new Pair(succProb[i], e[1]));
            graph.get(e[1]).add(new Pair(succProb[i], e[0]));
        }

        PriorityQueue<Pair> que = new PriorityQueue<Pair>();
        double[] prob = new double[n];

        que.offer(new Pair(1, start));
        prob[start] = 1;
        while (!que.isEmpty()) {
            Pair pair = que.poll();
            double pr = pair.probability;
            int node = pair.node;
            if (pr < prob[node]) {
                continue;
            }
            for (Pair pairNext : graph.get(node)) {
                double prNext = pairNext.probability;
                int nodeNext = pairNext.node;
                if (prob[nodeNext] < prob[node] * prNext) {
                    prob[nodeNext] = prob[node] * prNext;
                    que.offer(new Pair(prob[nodeNext], nodeNext));
                }
            }
        }
        return prob[end];
    }
}

class Pair implements Comparable<Pair> {
    double probability;
    int node;

    public Pair(double probability, int node) {
        this.probability = probability;
        this.node = node;
    }

    public int compareTo(Pair pair2) {
        if (this.probability == pair2.probability) {
            return this.node - pair2.node;
        } else {
            return this.probability - pair2.probability > 0 ? -1 : 1;
        }
    }
}

[sol1-Python3]

class Solution:
    def maxProbability(self, n: int, edges: List[List[int]], succProb: List[float], start: int, end: int) -> float:
        graph = collections.defaultdict(list)
        for i, (x, y) in enumerate(edges):
            graph[x].append((succProb[i], y))
            graph[y].append((succProb[i], x))
        
        que = [(-1.0, start)]
        prob = [0.0] * n
        prob[start] = 1.0

        while que:
            pr, node = heapq.heappop(que)
            pr = -pr
            if pr < prob[node]:
                continue
            for prNext, nodeNext in graph[node]:
                if prob[nodeNext] < prob[node] * prNext:
                    prob[nodeNext] = prob[node] * prNext
                    heapq.heappush(que, (-prob[nodeNext], nodeNext))
        
        return prob[end]

复杂度分析

• 时间复杂度：O(m \log m)，其中 m 是图中边的数量。如果不使用任何优化，时间复杂度是 O(mn)，其中 n 是图中点的数量。使用不同的数据结构优化，将会表现出不同的时间复杂度：

  • 优先队列（例如 C++ 中的 priority_queue）优化：O(m \log m)；
  • 手写堆优化：O(m \log n)；
  • 线段树优化：O(m \log n)；
  • 斐波那契堆优化：O(n \log n + m)。

• 空间复杂度：O(m)，其中 m 是图中边的数量。

正确性证明

对原图 G 中的每条边权取对数，这样就得到了一个边权在 (-\infty ,0] 中的图 G’，图 G 中「从起点到终点成功概率最大」的路径对应了图 G’ 中「从起点到终点边权和最大」的路径。将图 G’ 的边权取相反数得到图 G’’，它的边权在 [0, \infty) 中，这样图 G’ 中「从起点到终点边权和最大」的路径变成了图 G’’ 中「从起点到终点边权和最小」的路径。由于图 G’’ 中没有负权边，因此可以使用 Dijkstra 算法找出「从起点到终点边权和最小」的路径，这样也就找出了图 G 中「从起点到终点成功概率最大」的路径。