1519-子树中标签相同的节点数
给你一棵树(即,一个连通的无环无向图),这棵树由编号从 0 到 n - 1 的 n 个节点组成,且恰好有 n - 1 条 edges
。树的根节点为节点 0 ,树上的每一个节点都有一个标签,也就是字符串 labels 中的一个小写字符(编号为 i 的 节点的标签就是labels[i] )
边数组 edges 以 edges[i] = [ai, bi] 的形式给出,该格式表示节点 ai 和 bi 之间存在一条边。
返回一个大小为 n 的数组,其中 ans[i] 表示第 i 个节点的子树中与节点 i 标签相同的节点数。
树 T 中的子树是由 T 中的某个节点及其所有后代节点组成的树。
示例 1:
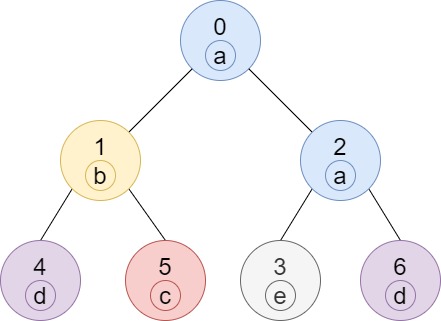
**输入:** n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], labels = "abaedcd"
**输出:** [2,1,1,1,1,1,1]
**解释:** 节点 0 的标签为 'a' ,以 'a' 为根节点的子树中,节点 2 的标签也是 'a' ,因此答案为 2 。注意树中的每个节点都是这棵子树的一部分。
节点 1 的标签为 'b' ,节点 1 的子树包含节点 1、4 和 5,但是节点 4、5 的标签与节点 1 不同,故而答案为 1(即,该节点本身)。
示例 2:
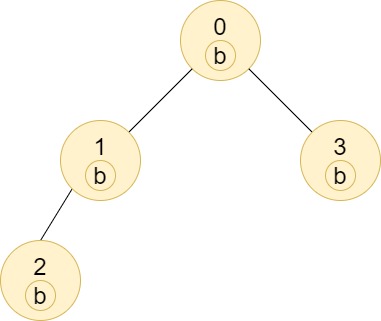
**输入:** n = 4, edges = [[0,1],[1,2],[0,3]], labels = "bbbb"
**输出:** [4,2,1,1]
**解释:** 节点 2 的子树中只有节点 2 ,所以答案为 1 。
节点 3 的子树中只有节点 3 ,所以答案为 1 。
节点 1 的子树中包含节点 1 和 2 ,标签都是 'b' ,因此答案为 2 。
节点 0 的子树中包含节点 0、1、2 和 3,标签都是 'b',因此答案为 4 。
示例 3:
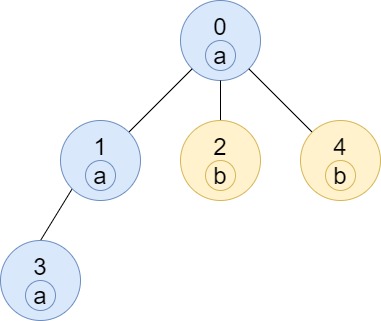
**输入:** n = 5, edges = [[0,1],[0,2],[1,3],[0,4]], labels = "aabab"
**输出:** [3,2,1,1,1]
提示:
1 <= n <= 10^5edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != bilabels.length == nlabels仅由小写英文字母组成
方法一:深度优先搜索
这道题中,树的表示方法是一个连通的无环无向图。树中包含编号从 0 到 n-1 的 n 个节点,其中根节点为节点 0,以及 n-1 条无向边。由于给出的边是无向的,因此不能直接从边的节点先后顺序判断父节点和子节点。
虽然给出的边是无向的,但是由于根节点已知,因此从根节点开始搜索,对每个访问到的节点标记为已访问,即可根据节点是否被访问过的信息知道相邻节点的父子关系。除了打访问标记外,还有一个办法可以解决这个问题,即在深度优先搜索的时候,把父节点当参数传入,即 depthFirstSearch(now, pre, ...) 的形式,其中 now 为当前节点,pre 为它的父节点,这样当邻接表中存的是无向图时,我们只要在拓展节点的时候判断 now 拓展到的节点等不等于 pre,即可避免再次拓展到父节点。下面 Java 代码中,给出前者的实现;C++ 和 Python 代码中,给出后者的实现。
这道题需要求出每个节点的子树中与该节点标签相同的节点数,即该节点的子树中,该节点标签出现的次数。由于一个节点的子树中可能包含任意的标签,因此需要对每个节点记录该节点的子树中的所有标签的出现次数。又由于标签一定是小写字母,因此只需要对每个节点维护一个长度为 26 的数组即可。
显然,一个节点的子树中的每个标签出现的次数,由该节点的左右子树中的每个标签出现的次数以及该节点自身的标签决定,因此可以使用深度优先搜索,递归地计算每个节点的子树中的每个标签出现的次数。
当得到一个节点的子树中的每个标签出现的次数之后,即可根据该节点的标签,得到子树中与该节点标签相同的节点数。
1 | class Solution { |
1 | class Solution { |
1 | class Solution: |
复杂度分析
时间复杂度:O(nc),其中 n 是树中的节点数,c 是字符集大小,此处 c = 26。深度优先搜索需要对树中的每个节点访问一次,对每个节点都需要更新所有可能的标签出现的次数,由于标签都是小写字母,需要对 26 个字母都进行一次讨论。
空间复杂度:O(nc),其中 n 是树中的节点数。空间复杂度主要取决于递归栈的调用深度,递归栈的调用深度不会超过 n。