1528-重新排列字符串

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:30 2023-09-13 16:06:30 Updated    

给你一个字符串 s 和一个 长度相同 的整数数组 indices 。

请你重新排列字符串 s ，其中第 i 个字符需要移动到 indices[i] 指示的位置。

返回重新排列后的字符串。

示例 1：

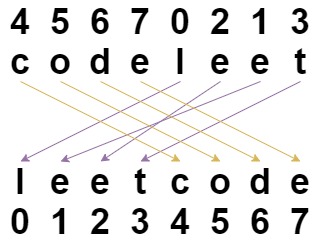
**输入：** s = "codeleet", indices = [4,5,6,7,0,2,1,3]
**输出：** "leetcode"
**解释：** 如图所示，"codeleet" 重新排列后变为 "leetcode" 。

示例 2：

**输入：** s = "abc", indices = [0,1,2]
**输出：** "abc"
**解释：** 重新排列后，每个字符都还留在原来的位置上。

提示：

  • s.length == indices.length == n
  • 1 <= n <= 100
  • s 仅包含小写英文字母
  • 0 <= indices[i] < n
  • indices 的所有的值都是 唯一 的

方法一：模拟

思路与算法

创建一个新字符串 result 来存储答案。对于 s 每个下标 i，将 result}[\textit{indices}[i]] 处的字符设成 s[i] 即可。

代码

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    string restoreString(string s, vector<int>& indices) {
        int length = s.length();
        string result(length, 0);

        for(int i = 0; i < length; i++) {
            result[indices[i]] = s[i];
        }
        return result;
    }
};
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public String restoreString(String s, int[] indices) {
        int length = s.length();
        char[] result = new char[length];

        for (int i = 0; i < length; i++) {
            result[indices[i]] = s.charAt(i);
        }
        return new String(result);
    }
}
[sol1-JavaScript]
1
2
3
4
5
6
7
8
9
10
var restoreString = function(s, indices) {
    const length = s.length;
    const result = new Array(length);
    
    for (let i = 0; i < length; ++i) {
        result[indices[i]] = s.charAt(i);
    }
    
    return result.join('');
};
[sol1-Python3]
1
2
3
4
5
6
7
class Solution:
    def restoreString(self, s: str, indices: List[int]) -> str:
        length = len(s)
        result = [""] * length
        for i, ch in enumerate(s):
            result[indices[i]] = ch
        return "".join(result)

复杂度分析

  • 时间复杂度：O(N)，其中 N 为字符串 s 的长度。我们只需对字符串 s 执行一次线性扫描即可。

  • 空间复杂度：O(1) 或 O(N)。除开辟的存储答案的字符串外，我们只需要常数空间存放若干变量。如果使用的语言不允许对字符串进行修改，我们还需要 O(N) 的空间临时存储答案。

方法二：原地修改

思路与算法

本题也可以通过原地修改输入数据的方式来求解。

直观的想法是：对于下标 i，需要把字符 s[i] 移动到 indices}[i] 的位置上；然后，我们前进到位置 indices}[i]，并将字符 s[\textit{indices}[i]] 移动到 indices}[\textit{indices}[i]] 的位置上。类似的过程以此类推，直到最终回到起点 i。此时，封闭路径 i \to \textit{indices}[i] \to \textit{indices}[\textit{indices}[i]] \to … \to i 上的所有字符，都已经被设置成正确的值。

我们只要找到 indices}[i] 中所有这样的封闭路径，并进行对应的移动操作，就能够得到最终的答案。

这样做有一个小小的问题：当在第二步试图把字符 s[\textit{indices}[i]] 移动到 indices}[\textit{indices}[i]] 的位置上时，会发现字符 s[\textit{indices}[i]] 已经在第一步被覆写了。因此，在每一步移动前，需要先额外记录目标位置处字符的原有值。

另一个隐含的问题是如何避免处理重复的封闭路径。为了解决此问题，我们每处理一个封闭路径，就将该路径上的 indices 数组的值设置成下标自身。这样，当某个封闭路径被处理完毕后，扫描到该路径的另一个下标时，就不会处理该封闭路径了。

由于许多语言中的字符串类型都是不可更改的，实现原地修改较为麻烦，因此下面只给出 C++ 的参考代码。

代码

[sol2-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    string restoreString(string s, vector<int>& indices) {
        int length = s.length();
        for (int i = 0; i < length; i++) {
            if (indices[i] != i) {
                char ch = s[i]; // 当前需要被移动的字符
                int idx = indices[i]; // 该字符需要被移动的目标位置
                while (idx != i) {
                    swap(s[idx], ch); // 使用 swap 函数，在覆写 s[idx] 之前，先将其原始值赋给变量 ch
                    swap(indices[idx], idx); // 将封闭路径中的 indices 数组的值设置成下标自身
                }
                // 退出循环后，还要再覆写起点处的字符
                s[i] = ch;
                indices[i] = i;
            }
        }
        return s;
    }
};

复杂度分析

  • 时间复杂度：O(N)，其中 N 为字符串 s 的长度。尽管代码看上去有两层循环，但因为不会处理相同的封闭路径，每个下标实际上只被处理了一次，故时间复杂度是线性的。

  • 空间复杂度：O(1)。我们只需开辟常量大小的额外空间。

 Comments
On this page
1528-重新排列字符串