1530-好叶子节点对的数量

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:30 2023-09-13 16:06:30 Updated    

给你二叉树的根节点 root 和一个整数 distance 。

如果二叉树中两个 叶 节点之间的 最短路径长度 小于或者等于 distance ，那它们就可以构成一组 好叶子节点对 。

返回树中 好叶子节点对的数量 。

示例 1：

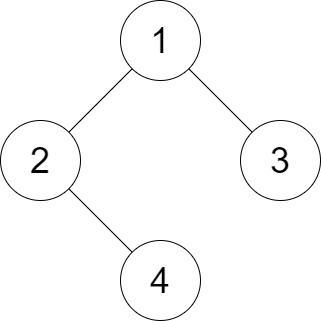
**输入：** root = [1,2,3,null,4], distance = 3
**输出：** 1
**解释：** 树的叶节点是 3 和 4 ，它们之间的最短路径的长度是 3 。这是唯一的好叶子节点对。

示例 2：

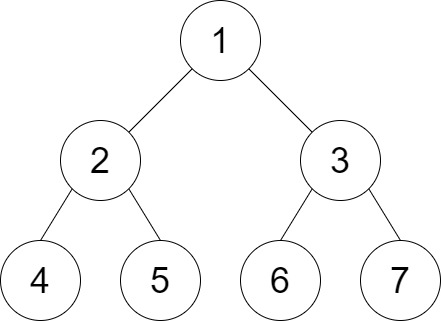
**输入：** root = [1,2,3,4,5,6,7], distance = 3
**输出：** 2
**解释：** 好叶子节点对为 [4,5] 和 [6,7] ，最短路径长度都是 2 。但是叶子节点对 [4,6] 不满足要求，因为它们之间的最短路径长度为 4 。

示例 3：

**输入：** root = [7,1,4,6,null,5,3,null,null,null,null,null,2], distance = 3
**输出：** 1
**解释：** 唯一的好叶子节点对是 [2,5] 。

示例 4：

**输入：** root = [100], distance = 1
**输出：** 0

示例 5：

**输入：** root = [1,1,1], distance = 2
**输出：** 1

提示：

  • tree 的节点数在 [1, 2^10] 范围内。
  • 每个节点的值都在 [1, 100] 之间。
  • 1 <= distance <= 10

方法一：递归

思路与算法

对于二叉树的任意两个不同的叶子节点 A、B，一个重要的性质是：它们之间有且仅有一条最短路径。设两个叶子节点的最近公共祖先为 P，则最短路径的长度，等于 A 到 P 的距离，加上 B 到 P 的距离。

于是，我们遍历所有非叶子节点 P，找到以 P 为最近公共祖先的所有叶子节点对，并根据上面的等式，计算每一对之间的距离，并统计距离不超过 distance 的节点对数目，就能够得到最终的答案。

那么怎么计算每个叶子节点对之间的距离呢？关键是要知道：以 P 为根节点的子树中的所有叶子节点，它们与 P 之间的距离。于是，对于任意的节点 P，我们先通过递归的方式，统计叶子节点与 P 的左孩子 left、右孩子 right 之间的距离；这样，两个以 P 为最近公共祖先的叶子节点 A、B，其中一个（例如 A）在以 left 为根的子树中，另一个（例如 B）在以 right 为根的子树中。A 与 B 之间的距离，就等于 A 与 left 之间的距离，加上 B 与 right 之间的距离，再加上 2。

由于本题中约束 distance} \le 10，因此对于每个非叶子节点 P，只需开辟长度为 distance}+1 的数组 depths，其中 depths}[i] 表示与 P 之间的距离为 i 的叶子节点数目。

代码

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
public:
    // 对于 dfs(root,distance)，同时返回：
    // 1）每个叶子节点与 root 之间的距离
    // 2) 以 root 为根节点的子树中好叶子节点对的数量
    pair<vector<int>, int> dfs(TreeNode* root, int distance) {
        vector<int> depths(distance + 1, 0);
        bool isLeaf = (!root->left && !root->right);
        if (isLeaf) { 
            depths[0] = 1;
            return make_pair(depths, 0);
        }

        vector<int> leftDepths(distance + 1, 0), rightDepths(distance + 1, 0);
        int leftCount = 0, rightCount = 0;
        if (root->left) {
            tie(leftDepths, leftCount) = dfs(root->left, distance);
        }
        if (root->right) {
            tie(rightDepths, rightCount) = dfs(root->right, distance);
        }

        for (int i = 0; i < distance; i++) {
            depths[i + 1] += leftDepths[i];
            depths[i + 1] += rightDepths[i];
        }

        int cnt = 0;
        for (int i = 0; i <= distance; i++) {
            for (int j = 0; j + i + 2 <= distance; j++) {
                cnt += (leftDepths[i] * rightDepths[j]);
            }
        }
        return make_pair(depths, cnt + leftCount + rightCount);
    }

    int countPairs(TreeNode* root, int distance) {
        auto [depths, ret] = dfs(root, distance);
        return ret;
    }
};
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
class Solution {
    public int countPairs(TreeNode root, int distance) {
        Pair pair = dfs(root, distance);
        return pair.count;
    }

    // 对于 dfs(root,distance)，同时返回：
    // 1）每个叶子节点与 root 之间的距离
    // 2) 以 root 为根节点的子树中好叶子节点对的数量
    public Pair dfs(TreeNode root, int distance) {
        int[] depths = new int[distance + 1];
        boolean isLeaf = root.left == null && root.right == null;
        if (isLeaf) { 
            depths[0] = 1;
            return new Pair(depths, 0);
        }

        int[] leftDepths = new int[distance + 1];
        int[] rightDepths = new int[distance + 1];
        int leftCount = 0, rightCount = 0;
        if (root.left != null) {
            Pair leftPair = dfs(root.left, distance);
            leftDepths = leftPair.depths;
            leftCount = leftPair.count;
        }
        if (root.right != null) {
            Pair rightPair = dfs(root.right, distance);
            rightDepths = rightPair.depths;
            rightCount = rightPair.count;
        }

        for (int i = 0; i < distance; i++) {
            depths[i + 1] += leftDepths[i];
            depths[i + 1] += rightDepths[i];
        }

        int cnt = 0;
        for (int i = 0; i <= distance; i++) {
            for (int j = 0; j + i + 2 <= distance; j++) {
                cnt += leftDepths[i] * rightDepths[j];
            }
        }
        return new Pair(depths, cnt + leftCount + rightCount);
    }
}

class Pair {
    int[] depths;
    int count;

    public Pair(int[] depths, int count) {
        this.depths = depths;
        this.count = count;
    }
}
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution:
    def countPairs(self, root: TreeNode, distance: int) -> int:
        # 对于 dfs(root,distance)，同时返回：
        # 每个叶子节点与 root 之间的距离
        # 以 root 为根节点的子树中好叶子节点对的数量
        def dfs(root: TreeNode, distance: int) -> (List[int], int):
            depths = [0] * (distance + 1)
            isLeaf = not root.left and not root.right
            if isLeaf:
                depths[0] = 1
                return (depths, 0)
            
            leftDepths, rightDepths = [0] * (distance + 1), [0] * (distance + 1)
            leftCount = rightCount = 0

            if root.left:
                leftDepths, leftCount = dfs(root.left, distance)
            if root.right:
                rightDepths, rightCount = dfs(root.right, distance)
            
            for i in range(distance):
                depths[i + 1] += leftDepths[i]
                depths[i + 1] += rightDepths[i]
            
            cnt = 0
            for i in range(distance + 1):
                for j in range(distance - i - 1):
                    cnt += leftDepths[i] * rightDepths[j]
            
            return (depths, cnt + leftCount + rightCount)
        

        _, ret = dfs(root, distance)
        return ret

复杂度分析

  • 时间复杂度：O(N \cdot \textit{distance}^2)，其中 N 为树中节点的数量。对于每个节点，我们至多需要遍历 O(\textit{distance}^2) 种好叶子节点对。

  • 空间复杂度：O(H \cdot \textit{distance})，其中 H 为树的高度。对于每个节点，我们都需要额外开辟 O(\textit{distance}) 的空间，而栈的最大深度为 O(H)。

 Comments
On this page
1530-好叶子节点对的数量