1535-找出数组游戏的赢家

给你一个由 不同 整数组成的整数数组 arr 和一个整数 k 。

每回合游戏都在数组的前两个元素（即 arr[0] 和 arr[1] ）之间进行。比较 arr[0] 与 arr[1]
的大小，较大的整数将会取得这一回合的胜利并保留在位置 0 ，较小的整数移至数组的末尾。当一个整数赢得 k 个连续回合时，游戏结束，该整数就是比赛的
赢家 。

返回赢得比赛的整数。

题目数据 保证 游戏存在赢家。

示例 1：

**输入：** arr = [2,1,3,5,4,6,7], k = 2
**输出：** 5
**解释：** 一起看一下本场游戏每回合的情况：
![](https://assets.leetcode-cn.com/aliyun-lc-upload/uploads/2020/07/30/q-example.png)
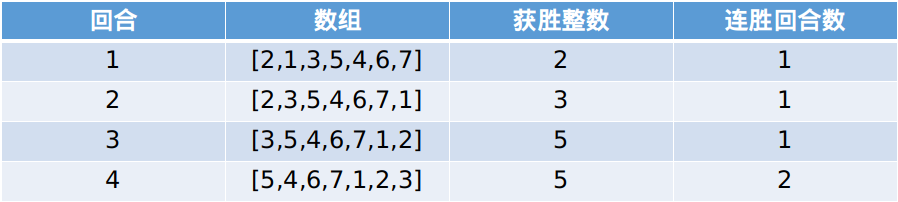
因此将进行 4 回合比赛，其中 5 是赢家，因为它连胜 2 回合。

示例 2：

**输入：** arr = [3,2,1], k = 10
**输出：** 3
**解释：** 3 将会在前 10 个回合中连续获胜。

示例 3：

**输入：** arr = [1,9,8,2,3,7,6,4,5], k = 7
**输出：** 9

示例 4：

**输入：** arr = [1,11,22,33,44,55,66,77,88,99], k = 1000000000
**输出：** 99

提示：

• 2 <= arr.length <= 10^5
• 1 <= arr[i] <= 10^6
• arr 所含的整数 各不相同 。
• 1 <= k <= 10^9

方法一：模拟

由于数组 arr 中的整数各不相同，因此数组中的任意两个整数之间的游戏一定能分出胜负。

首先考虑 k=1 的情况，当 k=1 时，只有 arr}[0] 和 arr}[1] 之间有一回合游戏，由于一定能分出胜负，因此直接返回 arr}[0] 和 arr}[1] 中的最大值即可。

然后考虑 k>1 的情况。根据题目描述，每回合游戏之后，较小的整数移至数组的末尾。其实，并不需要对数组进行更新。在第一回合游戏之后，无论 arr}[0] 和 arr}[1] 当中谁取得胜利，第二回合游戏的另一个整数一定是 arr 中的下一个整数。推广到一般的情况，当 2 \le i < \textit{arr}.\text{length 时，第 i 回合游戏一定在第 i-1 回合游戏中取得胜利的整数和 arr}[i] 之间进行。

因此，需要记录上一回合游戏中取得胜利的整数和该整数取得连续胜利的回合数。使用 prev 表示上一回合游戏中取得胜利的整数，使用 consecutive 表示该整数取得连续胜利的回合数。

第一回合游戏在 arr}[0] 和 arr}[1] 之间进行，第一回合游戏之后，prev 为 arr}[0] 和 arr}[1] 中的较大值，consecutive 的值为 1。

当 2 \le i < \textit{arr}.\text{length 时，令 curr}=\textit{arr}[i]，第 i 回合游戏在 prev 和 curr 之间进行，可能有以下两种情况：

• 如果 prev}>\textit{curr，则 prev 不变，将 consecutive 的值加 1，如果 consecutive 的值更新之后等于 k，则 prev 赢得 k 个连续回合，成为游戏的赢家，将 prev 返回即可；

• 如果 prev}<\textit{curr，则 curr 取得胜利，令 prev}=\textit{curr，并将 consecutive 的值更新为 1。

在上述过程中，同时维护数组 arr 中的最大值 maxNum。

如果遍历 arr 之后仍未发现有整数赢得 k 个连续回合，则不需要继续模拟，数组 arr 中的最大值 maxNum 即为游戏的赢家。

为什么不需要继续模拟就能知道 maxNum 为游戏的赢家？因为 maxNum 是数组 arr 中的最大值，无论和哪个整数进行游戏，maxNum 都能取得胜利，因此在遍历 arr 之后，maxNum 一定位于 arr}[0]，且将一直位于 arr}[0]，在其余的游戏中，maxNum 将永远取得胜利，自然也会赢得 k 个连续回合。

[sol1-Java]

class Solution {
    public int getWinner(int[] arr, int k) {
        int prev = Math.max(arr[0], arr[1]);
        if (k == 1) {
            return prev;
        }
        int consecutive = 1;
        int maxNum = prev;
        int length = arr.length;
        for (int i = 2; i < length; i++) {
            int curr = arr[i];
            if (prev > curr) {
                consecutive++;
                if (consecutive == k) {
                    return prev;
                }
            } else {
                prev = curr;
                consecutive = 1;
            }
            maxNum = Math.max(maxNum, curr);
        }
        return maxNum;
    }
}

[sol1-C++]

class Solution {
public:
    int getWinner(vector<int>& arr, int k) {
        int prev = max(arr[0], arr[1]);
        if (k == 1) {
            return prev;
        }
        int consecutive = 1;
        int maxNum = prev;
        int length = arr.size();
        for (int i = 2; i < length; i++) {
            int curr = arr[i];
            if (prev > curr) {
                consecutive++;
                if (consecutive == k) {
                    return prev;
                }
            } else {
                prev = curr;
                consecutive = 1;
            }
            maxNum = max(maxNum, curr);
        }
        return maxNum;
    }
};

[sol1-Python3]

class Solution:
    def getWinner(self, arr: List[int], k: int) -> int:
        prev = max(arr[0], arr[1])
        if k == 1:
            return prev

        consecutive = 1
        maxNum = prev
        length = len(arr)

        for i in range(2, length):
            curr = arr[i]
            if prev > curr:
                consecutive += 1
                if consecutive == k:
                    return prev
            else:
                prev = curr
                consecutive = 1
            maxNum = max(maxNum, curr)
        
        return maxNum

复杂度分析

• 时间复杂度：O(n)，其中 n 是字符串 arr 的长度。遍历数组一次。

• 空间复杂度：O(1)。只需要维护常量的额外空间。