1537-最大得分
你有两个 有序 且数组内元素互不相同的数组 nums1 和 nums2 。
一条 合法路径 定义如下:
- 选择数组 nums1 或者 nums2 开始遍历(从下标 0 处开始)。
- 从左到右遍历当前数组。
- 如果你遇到了
nums1和nums2中都存在的值,那么你可以切换路径到另一个数组对应数字处继续遍历(但在合法路径中重复数字只会被统计一次)。
得分定义为合法路径中不同数字的和。
请你返回所有可能合法路径中的最大得分。
由于答案可能很大,请你将它对 10^9 + 7 取余后返回。
示例 1:
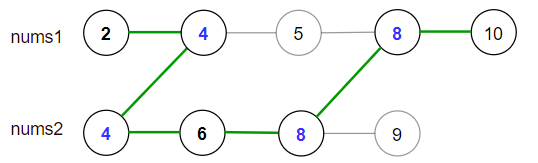
**输入:** nums1 = [2,4,5,8,10], nums2 = [4,6,8,9]
**输出:** 30
**解释:** 合法路径包括:
[2,4,5,8,10], [2,4,5,8,9], [2,4,6,8,9], [2,4,6,8,10],(从 nums1 开始遍历)
[4,6,8,9], [4,5,8,10], [4,5,8,9], [4,6,8,10] (从 nums2 开始遍历)
最大得分为上图中的绿色路径 **[2,4,6,8,10]** 。
示例 2:
**输入:** nums1 = [1,3,5,7,9], nums2 = [3,5,100]
**输出:** 109
**解释:** 最大得分由路径 **[1,3,5,100]** 得到。
示例 3:
**输入:** nums1 = [1,2,3,4,5], nums2 = [6,7,8,9,10]
**输出:** 40
**解释:** nums1 和 nums2 之间无相同数字。
最大得分由路径 **[6,7,8,9,10]** 得到。
示例 4:
**输入:** nums1 = [1,4,5,8,9,11,19], nums2 = [2,3,4,11,12]
**输出:** 61
提示:
1 <= nums1.length <= 10^51 <= nums2.length <= 10^51 <= nums1[i], nums2[i] <= 10^7nums1和nums2都是严格递增的数组。
方法一:动态规划
思路与算法
如果我们将相同的元素「合并」起来,就可以得到一个形状规则的有向无环图。以题目的示例一为例:
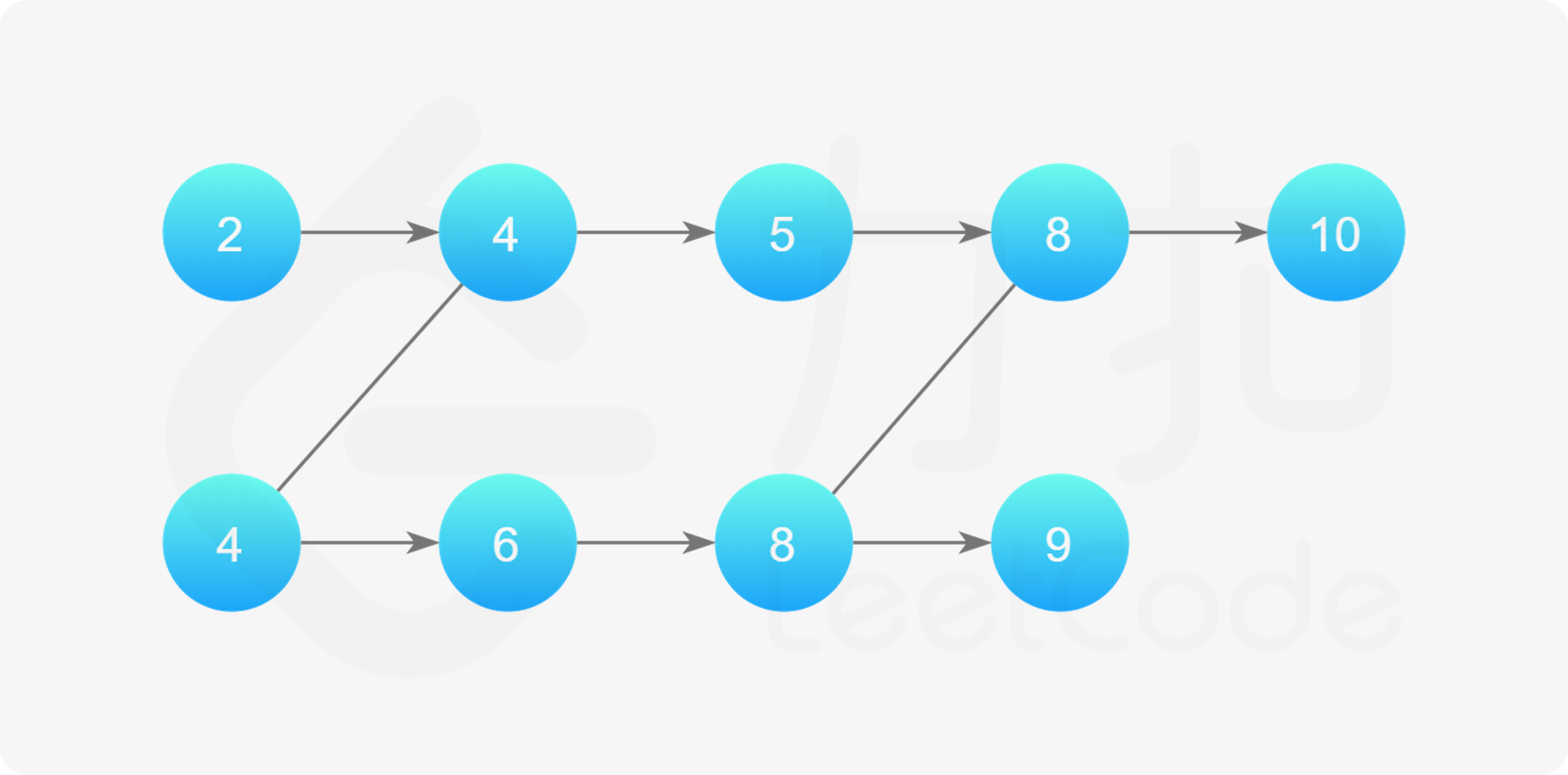 {:width=”74%”}
{:width=”74%”}
将相同的元素合并后,就可以得到如下的有向无环图:
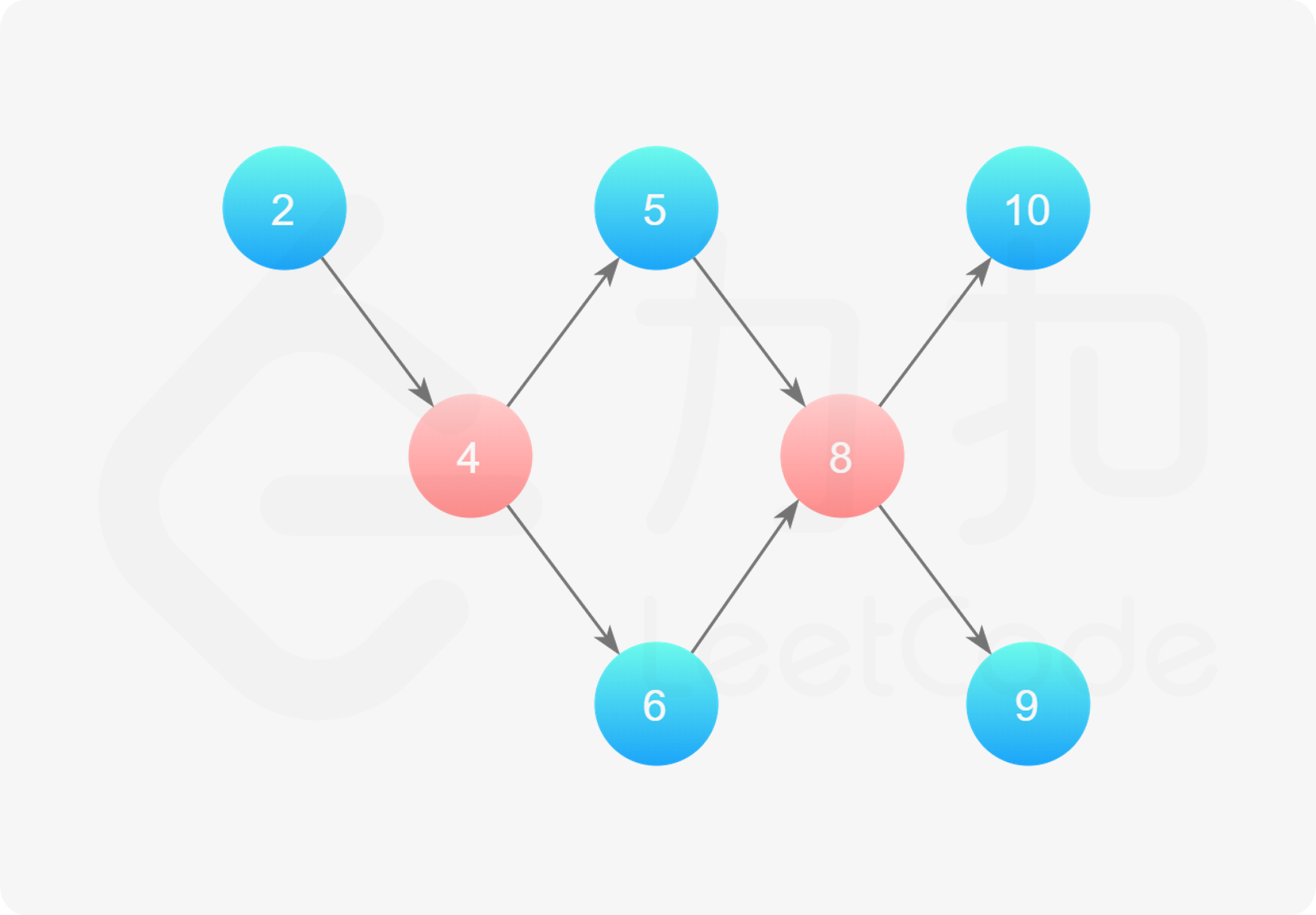 {:width=”70%”}
{:width=”70%”}
这样我们就可以使用动态规划解决本题了。我们用 f[i] 和 g[j] 分别表示遍历到数组 nums}_1[i] 和 nums}_2[j] 时的最大得分。如果遍历到的元素没有合并,那么它只会从相同数组的前一个元素转移而来:
\begin{aligned}
f[i] &= f[i-1] + \textit{nums}_1[i] \
g[j] &= g[j-1] + \textit{nums}_2[j]
\end{aligned}
如果遍历到的元素合并了,例如 nums}_1[i] = \textit{nums}_2[j],那么它可以从任意一个数组中对应位置的前一个元素转移而来,我们选择其中的较大值:
f[i] = g[j] = \max{(f[i-1], g[j-1])} + \textit{nums}_1[i]
最终的答案即为 f[m-1] 与 g[n-1] 中的较大值,其中 m 和 n 分别是数组 nums}_1 和 nums}_2 的长度。
细节
状态转移方程看似很简单,但我们应该根据什么顺序进行状态转移呢?由于我们只能「在同一个数组中从左向右进行遍历」或者「在有相同元素的前提下跳到另一个数组进行遍历」,所以我们遍历的路径上的元素总是单调递增的。
因此,我们可以按照数组 nums}_1 和 nums}_2 中所有元素从小到大的顺序进行状态转移。由于这两个数组本身已经是有序(单调递增)的,所以我们可以通过类似对两个数组进行「归并排序」的方法,即:
使用两个指针 i 和 j 分别指向数组 nums}_1 和 nums}_2 的首元素;
每次在进行状态转移前,比较 nums}_1[i] 的 nums}_2[i] 的大小关系。如果前者较小,那么对前者进行状态转移:
f[i] = f[i-1] + \textit{nums}_1[i]
如果后者较小,那么对后者进行状态转移:
g[j] = g[j-1] + \textit{nums}_2[j]
如果两者相等,那么同时进行状态转移:
f[i] = g[j] = \max{(f[i-1], g[j-1])} + \textit{nums}_1[i]
对于进行了状态转移的指针,将其向后移动一个位置。
这样一来,我们就可以顺利地完成动态规划并得到答案。注意到在进行状态转移时,f[i] 和 g[j] 只会从 f[i-1] 和 g[j-1] 转移而来,因此我们并不需要使用两个一维数组来存放动态规划的结果。我们可以仅使用两个变量 best}_1 和 best}_2 进行转移:
\begin{cases}
\textit{best}_1 = \textit{best}_1 + \textit{nums}_1[i] \
\textit{best}_2 = \textit{best}_2 + \textit{nums}_2[j] \
\textit{best}_1 = \textit{best}_2 = \max ( \textit{best}_1, \textit{best}_2 ) + \textit{nums}_1[i]
\end{cases}
它们的初始值均为 0。
代码
1 | class Solution { |
1 | class Solution { |
1 | class Solution: |
1 | const int MOD = 1000000007; |
复杂度分析
时间复杂度:O(m+n),其中 m 和 n 分别是数组 nums}_1 和 nums}_2 的长度。
空间复杂度:O(1)。