1569-将子数组重新排序得到同一个二叉搜索树的方案数

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:15:46 2023-09-13 16:15:46 Updated    

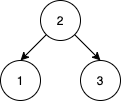
给你一个数组 nums 表示 1 到 n 的一个排列。我们按照元素在 nums
中的顺序依次插入一个初始为空的二叉搜索树（BST）。请你统计将 nums 重新排序后，统计满足如下条件的方案数：重排后得到的二叉搜索树与 nums
原本数字顺序得到的二叉搜索树相同。

比方说，给你 nums = [2,1,3]，我们得到一棵 2 为根，1 为左孩子，3 为右孩子的树。数组 [2,3,1] 也能得到相同的 BST，但
[3,2,1] 会得到一棵不同的 BST 。

请你返回重排 nums 后，与原数组 nums 得到相同二叉搜索树的方案数。

由于答案可能会很大，请将结果对 ** **10^9 + 7 取余数。

示例 1：

**输入：** nums = [2,1,3]
**输出：** 1
**解释：** 我们将 nums 重排， [2,3,1] 能得到相同的 BST 。没有其他得到相同 BST 的方案了。

示例 2：

![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/08/30/ex1.png)

**输入：** nums = [3,4,5,1,2]
**输出：** 5
**解释：** 下面 5 个数组会得到相同的 BST：
[3,1,2,4,5]
[3,1,4,2,5]
[3,1,4,5,2]
[3,4,1,2,5]
[3,4,1,5,2]

示例 3：

![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/08/30/ex4.png)

**输入：** nums = [1,2,3]
**输出：** 0
**解释：** 没有别的排列顺序能得到相同的 BST 。

提示：

  • 1 <= nums.length <= 1000
  • 1 <= nums[i] <= nums.length
  • nums 中所有数 互不相同 。

方法一：动态规划 + 组合计数

前言

方法一需要读者掌握如下内容：

  • 组合计数。在 n 个物品中选择 k 个（不计顺序）的方案数为 C_n^k，称之为「组合数」。组合数也可以写作 \binom{n}{k，计算公式为：

    C_n^k = \binom{n}{k} = n (n-1) \cdots (n-k+1) }{k!} = n!}{k!(n-k)!}

    这里定义 0!=1，那么有 C_n^0 = C_n^n = 1。

    组合数也可以通过递推求出：

    C_n^k = C_{n-1}^k + C_{n-1}^{k-1}

    直观上来看，从 n 个物品中选择 k 个的方案数，等于从前 n-1 个物品中选择 k 个的方案数，加上从前 n-1 个物品中选择 k-1 个（再选上第 n 个物品）的方案数之和。

思路与算法

我们不妨先根据数组 nums 把整棵二叉查找树 T 建立出来。

设某个满足要求的排列为 a_0, a_1, \cdots, a_{n-1，那么 a_0 必然是树 T 的根节点的元素，也就是 nums}[0]。

根据二叉查找树的性质，数组 nums 中小于 a_0 的元素会全部出现在根节点的左子树中，而数组 nums 中大于 a_0 的元素会全部出现在根节点的右子树中：

  • 左子树即为将数组 nums 中小于 a_0 的元素按照它们的出现顺序，依次插入一棵空的二叉查找树得到的结果；

  • 右子树即为将数组 nums 中大于 a_0 的元素按照它们的出现顺序，依次插入一棵空的二叉查找树得到的结果。

这样一来，我们就将原始问题转化成了两个规模更小但完全相同的子问题，因此我们可以尝试使用动态规划来解决本题。

我们设 f[a_i] 表示对于树 T 中以元素 a_i（对应的节点）为根节点的子树，将其中包含的所有元素进行重排列，并按照顺序依次插入一棵空的二叉查找树，可以得到和该子树相同结果的排列数。对于 a_i 而言，如果其左子树为 a_{il，右子树为 a_{ir，并且我们已经求出了 f[a_{il}] 以及 f[a_{ir}] 的值，那么：

  • 设以 a_i 为根节点的子树对应的排列的长度为 size}(a_i)；

  • 排列的首个元素为 a_i；

  • 我们需要在剩余的 size}(a_i) - 1 个位置中，选择 size}(a_{il}) 个位置用来放置左子树中的元素，剩余 size}(a_i) - 1 - \text{size}(a_{il}) = \text{size}(a_{ir}) 个位置用来放置右子树中的元素。

由于在 size}(a_i)-1 个位置中选择 size}(a_{il}) 个位置的方案数为 C_{\text{size}(a_i)-1}^{\text{size}(a_{il})，左子树的排列数为 f[a_{il}]，右子树的排列数为 f[a_{ir}]，根据乘法原理，可以得到状态转移方程为：

f[a_i] = C_{\text{size}(a_i)-1}^{\text{size}(a_{il})} \cdot f[a_{il}] \cdot f[a_{ir}]

如果 a_i 的某个子树为空，那么对应的 size 值为 0，f 值为 1。最终的答案即为 f[a_0]。

由于我们需要将答案对 10^9+7 进行取模，直接计算组合数的公式中包含除法，处理起来十分麻烦。因此我们可以使用递推的方法预处理出所有需要用到的组合数 C_{n’}^k，其中 0 \leq n’ < n，0 \leq k \leq n’。

代码

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
struct TNode {
    TNode* left;
    TNode* right;
    int value;
    int size;
    int ans;
    
    TNode(int val): left(nullptr), right(nullptr), value(val), size(1), ans(0) {}
};

class Solution {
private:
    static constexpr int mod = 1000000007;
    vector<vector<int>> c;

public:
    void insert(TNode* root, int val) {
        TNode* cur = root;
        while (true) {
            ++cur->size;
            if (val < cur->value) {
                if (!cur->left) {
                    cur->left = new TNode(val);
                    return;
                }
                cur = cur->left;
            }
            else {
                if (!cur->right) {
                    cur->right = new TNode(val);
                    return;
                }
                cur = cur->right;
            }
        }
    }

    void dfs(TNode* node) {
        if (!node) {
            return;
        }
        dfs(node->left);
        dfs(node->right);
        int lsize = node->left ? node->left->size : 0;
        int rsize = node->right ? node->right->size : 0;
        int lans = node->left ? node->left->ans : 1;
        int rans = node->right ? node->right->ans : 1;
        node->ans = (long long)c[lsize + rsize][lsize] % mod * lans % mod * rans % mod;
    }

    int numOfWays(vector<int>& nums) {
        int n = nums.size();
        if (n == 1) {
            return 0;
        }

        c.assign(n, vector<int>(n));
        c[0][0] = 1;
        for (int i = 1; i < n; ++i) {
            c[i][0] = 1;
            for (int j = 1; j < n; ++j) {
                c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % mod;
            }
        }

        TNode* root = new TNode(nums[0]);
        for (int i = 1; i < n; ++i) {
            int val = nums[i];
            insert(root, val);
        }

        dfs(root);
        return (root->ans - 1 + mod) % mod;
    }
};
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
class Solution {
    static final int MOD = 1000000007;
    long[][] c;

    public int numOfWays(int[] nums) {
        int n = nums.length;
        if (n == 1) {
            return 0;
        }

        c = new long[n][n];
        c[0][0] = 1;
        for (int i = 1; i < n; ++i) {
            c[i][0] = 1;
            for (int j = 1; j < n; ++j) {
                c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % MOD;
            }
        }

        TreeNode root = new TreeNode(nums[0]);
        for (int i = 1; i < n; ++i) {
            int val = nums[i];
            insert(root, val);
        }

        dfs(root);
        return (root.ans - 1 + MOD) % MOD;
    }

    public void insert(TreeNode root, int value) {
        TreeNode cur = root;
        while (true) {
            ++cur.size;
            if (value < cur.value) {
                if (cur.left == null) {
                    cur.left = new TreeNode(value);
                    return;
                }
                cur = cur.left;
            } else {
                if (cur.right == null) {
                    cur.right = new TreeNode(value);
                    return;
                }
                cur = cur.right;
            }
        }
    }

    public void dfs(TreeNode node) {
        if (node == null) {
            return;
        }
        dfs(node.left);
        dfs(node.right);
        int lsize = node.left != null ? node.left.size : 0;
        int rsize = node.right != null ? node.right.size : 0;
        int lans = node.left != null ? node.left.ans : 1;
        int rans = node.right != null ? node.right.ans : 1;
        node.ans = (int) (c[lsize + rsize][lsize] % MOD * lans % MOD * rans % MOD);
    }
}

class TreeNode {
    TreeNode left;
    TreeNode right;
    int value;
    int size;
    int ans;

    TreeNode(int value) {
        this.value = value;
        this.size = 1;
        this.ans = 0;
    }
}
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
class TNode:
    def __init__(self, val):
        self.left = None
        self.right = None
        self.value = val
        self.size = 1
        self.ans = 0

class Solution:
    def numOfWays(self, nums: List[int]) -> int:
        def insert(val: int):
            cur = root
            while True:
                cur.size += 1
                if val < cur.value:
                    if not cur.left:
                        cur.left = TNode(val)
                        return
                    cur = cur.left
                else:
                    if not cur.right:
                        cur.right = TNode(val)
                        return
                    cur = cur.right
        
        def dfs(node: TNode):
            if not node:
                return
            dfs(node.left)
            dfs(node.right)
            lsize = node.left.size if node.left else 0
            rsize = node.right.size if node.right else 0
            lans = node.left.ans if node.left else 1
            rans = node.right.ans if node.right else 1
            node.ans = c[lsize + rsize][lsize] * lans * rans % mod

        n = len(nums)
        if n == 1:
            return 0
        
        mod = 10**9 + 7
        c = [[0] * n for _ in range(n)]
        c[0][0] = 1
        for i in range(1, n):
            c[i][0] = 1
            for j in range(1, n):
                c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % mod

        root = TNode(nums[0])
        for i in range(1, n):
            val = nums[i]
            insert(val)

        dfs(root)
        return (root.ans - 1 + mod) % mod

复杂度分析

  • 时间复杂度：O(n^2)。时间复杂度由以下三部分组成：

    • 预处理组合数的时间复杂度为 O(n^2)；

    • 建立二叉查找树的平均时间复杂度为 O(n \log n)。但在最坏情况下，当数组 nums 中的数单调递增或递减时，二叉查找树退化成链式结构，建立的时间复杂度为 O(n^2)。

    • 动态规划的时间复杂度为 O(n)，即为对二叉查找树进行遍历需要的时间。

  • 空间复杂度：O(n^2)。

小贴士

上述 Python 代码的运行时间较长，具体的原因是 Python 对列表 list 的访问效率较低，预处理组合数耗费了大部分的时间。根据 Python 语言的特性，可以不对组合数进行预处理，而是使用 math.comb 或者 math.factorial 函数直接计算组合数，可以大大降低运行时间。但这里仍然希望读者能够掌握递推计算组合数的技巧。

方法二：并查集 + 乘法逆元优化

前言

方法二为竞赛难度，力求将方法一中的各个部分进行优化，达到更低的时间复杂度，供读者挑战自我。

方法二需要读者掌握如下内容：

  • 使用「路径压缩」和「按秩合并」优化的并查集，并且知道并查集实际上是一种树形结构。并查集为面试中常见的数据结构，关于这两种优化的资料也随处可得，故这里不再赘述。

  • 乘法逆元。设模数为 m，整数 a(0 < a < m) 在模 m 的意义下存在乘法逆元整数 b(0 < b < m)，当且仅当

    ab \equiv 1 ~ (\bmod ~ m)

    成立。当 m 为质数时，根据上式可得

    ab = km + 1, \quad k \in \mathbb{N}^+

    整理得

    b \cdot a - k \cdot m = 1

    根据「裴蜀定理」，由于 gcd}(a, m) = 1，因此必存在整数 b 和 k 使得上式成立。如果 (b_0, k_0) 是一组解，那么

    (b_0 + cm, k_0 + ca), \quad c \in \mathbb{Z}

    都是上式的解。因此必然存在一组解中的整数 b 满足 0 < b < m。

    那么如何求出 b 呢？一种简单的方法是使用「费马小定理」，即

    a^{m-1} \equiv 1 ~ (\bmod ~ m)

    那么有

    ab \equiv a^{m-1} ~ (\bmod ~ m)

    即

    b \equiv a^{m-2} ~ (\bmod ~ m)

    使用「乘法逆元」有什么好处呢？如果我们要求 c}{a 对 m 取模的结果，那么我们可以化除法为乘法，即

    c}{a} \equiv c \cdot b ~ (\bmod ~ m)

    这样一来，我们只要：

    • 预处理出所有 fac}[i] = i! \bmod m；

    • 预处理出所有 facInv}[i] = (i!)^{-1} = (i!)^{m-2} \bmod m。

    其中 (i!)^{-1 表示 i! 在模 m 意义下的乘法逆元，就可以快速计算出组合数：

    C_n^k = n!}{k!(n-k)!} \equiv \textit{fac}[n] \cdot \textit{facInv}[k] \cdot \textit{facInv}[n-k] ~ (\bmod ~ m)

    预处理的时间复杂度为 O(n \log m)，计算组合数的时间复杂度为 O(1)。如果读者不知道如何快速计算 (i!)^{m-2} \bmod m，可以参考 50. Pow(x, n) 的官方题解 。

    还能做到更快吗？答案是可以的。我们可以使用一个辅助数组 inv}[i] 表示数 i 的逆元 i^{-1，这样我们可以使用递推式

    \textit{facInv}[i] = \textit{facInv}[i-1] \cdot \textit{inv}[i]

    计算阶乘的乘法逆元。而 i^{-1 可以快速计算得到。设 m = u \cdot i + v，其中 (u, v) 是 m 除以 i 的商和余数，那么有：

    \begin{aligned}
    & u \cdot i + v = m \equiv 0 \
    \Leftrightarrow ~ & u + v \cdot i^{-1} \equiv 0 \
    \Leftrightarrow ~ & u \cdot v^{-1} + i^{-1} \equiv 0 \
    \Leftrightarrow ~ & i^{-1} \equiv -u \cdot v^{-1} ~ (\bmod ~ m)
    \end{aligned}

    由于 u = \lfloor m/i \rfloor，v = m % i，因此有

    \textit{inv}[i] \equiv -\lfloor m/i \rfloor \cdot \textit{inv}[m % i] ~ (\bmod ~ m)

    在实际的代码编写中，由于右侧为负数，因此可以将右侧加上 m \cdot \textit{inv}[m % i]，不会影响取模的结果，得到

    \textit{inv}[i] \equiv (m-\lfloor m/i \rfloor) \cdot \textit{inv}[m % i] ~ (\bmod ~ m)

    这样一来，预处理的时间复杂度降低为 O(n)，计算组合数的时间复杂度仍然为 O(1)。

思路与算法

在方法一中的「时间复杂度」部分，我们详细列举了每一部分需要的时间。现在我们已经将预处理组合数的时间复杂度降低至 O(n)，并且将空间复杂度从 O(n^2) 减少至 O(n)，那么接下来就需要降低建立二叉树的时间复杂度了。

可以发现，在方法一中我们并没有用到数组 nums 是 1 到 n 的一个排列这样的条件：只要数组 nums 中的元素互不相同，方法一都可以得到正确的结果。

对于两个相邻的整数 a_i 和 a_i-1，我们可以证明：

  • 如果 a_i 在数组 nums 中出现在 a_i-1 之前，那么 a_i-1 必然出现在 a_i 对应的节点的左子树中。这是因为 a_i-1 和 a_i 中没有其它的数出现在数组 nums 中，所以这两个数相较于其它的数要么同时较小，要么同时较大。因此在插入 a_i-1 时，会从根节点走到 a_i 对应的节点，再走到其左子树中；

    • 用相同的方法可以证明：对于两个相邻的整数 a_i 和 a_i+1，如果 a_i 在数组 nums 中出现在 a_i+1 之前，那么 a_i+1 必然出现在 a_i 对应的节点的右子树中。

  • 如果 a_i 在数组 nums 中出现在 a_i-1 之后，那么 a_i 对应的节点的左子树为空。这是因为 a_i-1 在数组 nums 中出现在 a_i 之前，根据上面的证明，a_i 必然出现在 a_i-1 对应的节点的右子树中，要想成为 a_i 对应的节点的左子树中的元素，必须要小于 a_i，但小于 a_i 的数一定都小于 a_i-1，会被 a_i-1 对应的节点「拦截」，因此 a_i 对应的节点的左子树为空。

    • 用相同的方法可以证明：如果 a_i 在数组 nums 中出现在 a_i+1 之后，那么 a_i+1 对应的节点的左子树为空。

这样一来，我们只需要逆序地遍历数组 nums 就可以快速地构造出整棵二叉查找树了。当我们遍历到 nums}[i] 时：

  • 如果 nums}[i]-1 已经遍历过，那么 nums}[i] 对应的节点的左子树，就是包含 nums}[i]-1 的树；否则 nums}[i] 的左子树为空；

  • 如果 nums}[i]+1 已经遍历过，那么 nums}[i] 对应的节点的右子树，就是包含 nums}[i]+1 的树；否则 nums}[i] 的右子树为空；

那么如何得到包含某个元素的树的根节点呢？在构造二叉查找树的同时，我们可以使用并查集维护当前遍历过的元素之间的连通性。在遍历数组 nums 并构造二叉查找树的过程中，元素 nums}[i .. n-1] 对应着若干棵二叉查找树，而每棵二叉查找树都一一对应着并查集中的一棵树。对于并查集中的每棵树，我们在其根节点上记录这棵树对应的二叉查找树的根节点，记为数组 root。这样对于任意一个元素，我们在并查集中查找到根，也就能得到其在二叉查找树中的根节点了。

通过并查集辅助二叉查找树的构造，时间复杂度可以降低至 O(n \alpha(n))。

细节

当我们需要合并并查集中的两个根节点 x 和 y 时，如何修改 root}[x] 和 root}[y] 呢？读者可以对这个问题进行思考，也可以参考下面的代码得出答案。

代码

[sol2-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
struct TNode {
    TNode* left;
    TNode* right;
    int size;
    int ans;
    
    TNode(): left(nullptr), right(nullptr), size(1), ans(0) {}
};

class UnionFind {
public:
    vector<int> parent, size, root;
    int n;
    
public:
    UnionFind(int _n): n(_n), parent(_n), size(_n, 1), root(_n) {
        iota(parent.begin(), parent.end(), 0);
        iota(root.begin(), root.end(), 0);
    }
    
    int findset(int x) {
        return parent[x] == x ? x : parent[x] = findset(parent[x]);
    }

    int getroot(int x) {
        return root[findset(x)];
    }
    
    void unite(int x, int y) {
        root[y] = root[x];
        if (size[x] < size[y]) {
            swap(x, y);
        }
        parent[y] = x;
        size[x] += size[y];
    }
    
    bool findAndUnite(int x, int y) {
        int x0 = findset(x);
        int y0 = findset(y);
        if (x0 != y0) {
            unite(x0, y0);
            return true;
        }
        return false;
    }
};

class Solution {
private:
    static constexpr int mod = 1000000007;
    vector<int> fac, inv, facInv;

public:
    int numOfWays(vector<int>& nums) {
        int n = nums.size();
        if (n == 1) {
            return 0;
        }

        fac.resize(n);
        inv.resize(n);
        facInv.resize(n);
        fac[0] = inv[0] = facInv[0] = 1;
        fac[1] = inv[1] = facInv[1] = 1;
        for (int i = 2; i < n; ++i) {
            fac[i] = (long long)fac[i - 1] * i % mod;
            inv[i] = (long long)(mod - mod / i) * inv[mod % i] % mod;
            facInv[i] = (long long)facInv[i - 1] * inv[i] % mod;
        }

        unordered_map<int, TNode*> found;
        UnionFind uf(n);
        for (int i = n - 1; i >= 0; --i) {
            int val = nums[i] - 1;
            TNode* node = new TNode();
            if (val > 0 && found.count(val - 1)) {
                int lchild = uf.getroot(val - 1);
                node->left = found[lchild];
                node->size += node->left->size;
                uf.findAndUnite(val, lchild);
            }
            if (val < n - 1 && found.count(val + 1)) {
                int rchild = uf.getroot(val + 1);
                node->right = found[rchild];
                node->size += node->right->size;
                uf.findAndUnite(val, rchild);
            }
            
            int lsize = node->left ? node->left->size : 0;
            int rsize = node->right ? node->right->size : 0;
            int lans = node->left ? node->left->ans : 1;
            int rans = node->right ? node->right->ans : 1;
            node->ans = (long long)fac[lsize + rsize] * facInv[lsize] % mod * facInv[rsize] % mod * lans % mod * rans % mod;
            found[val] = node;
        }

        return (found[nums[0] - 1]->ans - 1 + mod) % mod;
    }
};
[sol2-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
class Solution {
    static final int MOD = 1000000007;
    long[] fac;
    long[] inv;
    long[] facInv;

    public int numOfWays(int[] nums) {
        int n = nums.length;
        if (n == 1) {
            return 0;
        }

        fac = new long[n];
        inv = new long[n];
        facInv = new long[n];
        fac[0] = inv[0] = facInv[0] = 1;
        fac[1] = inv[1] = facInv[1] = 1;
        for (int i = 2; i < n; ++i) {
            fac[i] = fac[i - 1] * i % MOD;
            inv[i] = (MOD - MOD / i) * inv[MOD % i] % MOD;
            facInv[i] = facInv[i - 1] * inv[i] % MOD;
        }

        Map<Integer, TreeNode> found = new HashMap<Integer, TreeNode>();
        UnionFind uf = new UnionFind(n);
        for (int i = n - 1; i >= 0; --i) {
            int val = nums[i] - 1;
            TreeNode node = new TreeNode();
            if (val > 0 && found.containsKey(val - 1)) {
                int lchild = uf.getroot(val - 1);
                node.left = found.get(lchild);
                node.size += node.left.size;
                uf.findAndUnite(val, lchild);
            }
            if (val < n - 1 && found.containsKey(val + 1)) {
                int rchild = uf.getroot(val + 1);
                node.right = found.get(rchild);
                node.size += node.right.size;
                uf.findAndUnite(val, rchild);
            }
            
            int lsize = node.left != null ? node.left.size : 0;
            int rsize = node.right != null ? node.right.size : 0;
            int lans = node.left != null ? node.left.ans : 1;
            int rans = node.right != null ? node.right.ans : 1;
            node.ans = (int) (fac[lsize + rsize] * facInv[lsize] % MOD * facInv[rsize] % MOD * lans % MOD * rans % MOD);
            found.put(val, node);
        }

        return (found.get(nums[0] - 1).ans - 1 + MOD) % MOD;
    }
}

class TreeNode {
    TreeNode left;
    TreeNode right;
    int size;
    int ans;

    TreeNode() {
        size = 1;
        ans = 0;
    }
}

class UnionFind {
    public int[] parent;
    public int[] size;
    public int[] root;
    public int n;

    public UnionFind(int n) {
        this.n = n;
        parent = new int[n];
        size = new int[n];
        root = new int[n];
        Arrays.fill(size, 1);
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            root[i] = i;
        }
    }

    public int findset(int x) {
        return parent[x] == x ? x : (parent[x] = findset(parent[x]));
    }

    public int getroot(int x) {
        return root[findset(x)];
    }
    
    public void unite(int x, int y) {
        root[y] = root[x];
        if (size[x] < size[y]) {
            int temp = x;
            x = y;
            y = temp;
        }
        parent[y] = x;
        size[x] += size[y];
    }
    
    public boolean findAndUnite(int x, int y) {
        int x0 = findset(x);
        int y0 = findset(y);
        if (x0 != y0) {
            unite(x0, y0);
            return true;
        }
        return false;
    }
}
[sol2-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
class TNode:
    def __init__(self):
        self.left = None
        self.right = None
        self.size = 1
        self.ans = 0

class UnionFind:
    def __init__(self, n: int):
        self.n = n
        self.parent = list(range(n))
        self.root = list(range(n))
        self.size = [1] * n
    
    def findset(self, x: int) -> int:
        if self.parent[x] == x:
            return x
        self.parent[x] = self.findset(self.parent[x])
        return self.parent[x]
    
    def getroot(self, x: int) -> int:
        return self.root[self.findset(x)]
    
    def unite(self, x: int, y: int):
        self.root[y] = self.root[x]
        if self.size[x] < self.size[y]:
            x, y = y, x
        self.parent[y] = x
        self.size[x] += self.size[y]
    
    def findAndUnite(self, x: int, y: int) -> bool:
        parentX, parentY = self.findset(x), self.findset(y)
        if parentX != parentY:
            self.unite(parentX, parentY)
            return True
        return False

class Solution:
    def numOfWays(self, nums: List[int]) -> int:
        n = len(nums)
        if n == 1:
            return 0
        
        mod = 10**9 + 7
        fac = [0] * n
        inv = [0] * n
        facInv = [0] * n
        fac[0] = inv[0] = facInv[0] = 1
        fac[1] = inv[1] = facInv[1] = 1
        for i in range(2, n):
            fac[i] = fac[i - 1] * i % mod
            inv[i] = (mod - mod // i) * inv[mod % i] % mod
            facInv[i] = facInv[i - 1] * inv[i] % mod

        found = dict()
        uf = UnionFind(n)
        for i in range(n - 1, -1, -1):
            val = nums[i] - 1
            node = TNode()
            if val > 0 and val - 1 in found:
                lchild = uf.getroot(val - 1)
                node.left = found[lchild]
                node.size += node.left.size
                uf.findAndUnite(val, lchild)
            if val < n - 1 and val + 1 in found:
                rchild = uf.getroot(val + 1)
                node.right = found[rchild]
                node.size += node.right.size
                uf.findAndUnite(val, rchild)
            
            lsize = node.left.size if node.left else 0
            rsize = node.right.size if node.right else 0
            lans = node.left.ans if node.left else 1
            rans = node.right.ans if node.right else 1
            node.ans = fac[lsize + rsize] * facInv[lsize] * facInv[rsize] * lans * rans % mod;
            found[val] = node

        return (found[nums[0] - 1].ans - 1 + mod) % mod

复杂度分析

  • 时间复杂度：O(n \alpha(n))。

  • 空间复杂度：O(n)。

 Comments
On this page
1569-将子数组重新排序得到同一个二叉搜索树的方案数