1598-文件夹操作日志搜集器
每当用户执行变更文件夹操作时,LeetCode 文件系统都会保存一条日志记录。
下面给出对变更操作的说明:
"../":移动到当前文件夹的父文件夹。如果已经在主文件夹下,则 继续停留在当前文件夹 。"./":继续停留在当前文件夹 。"x/":移动到名为x的子文件夹中。题目数据 保证总是存在文件夹x。
给你一个字符串列表 logs ,其中 logs[i] 是用户在 ith 步执行的操作。
文件系统启动时位于主文件夹,然后执行 logs 中的操作。
执行完所有变更文件夹操作后,请你找出 返回主文件夹所需的最小步数 。
示例 1:

**输入:** logs = ["d1/","d2/","../","d21/","./"]
**输出:** 2
**解释:** 执行 "../" 操作变更文件夹 2 次,即可回到主文件夹
示例 2:
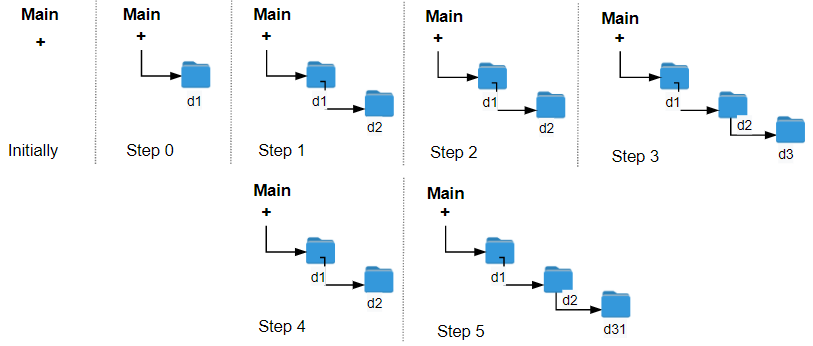
**输入:** logs = ["d1/","d2/","./","d3/","../","d31/"]
**输出:** 3
示例 3:
**输入:** logs = ["d1/","../","../","../"]
**输出:** 0
提示:
1 <= logs.length <= 1032 <= logs[i].length <= 10logs[i]包含小写英文字母,数字,'.'和'/'logs[i]符合语句中描述的格式- 文件夹名称由小写英文字母和数字组成
方法一:直接模拟
根据题意可知返回主文件夹的操作为连续退回到上一层目录,直到返回主目录为止,在这种操作下使用的操作数最少。我们用一个变量记录 depth 当前目录的层次深度,depth 初始化为 0,根据题意可知:
- 如果当前的操作为 “../“:移动到当前文件夹的父文件夹。如果已经在主文件夹下,则继续停留在当前文件夹。则此时如果层次深度 depth} > 0 则将 depth 减 1,否则 depth 保持不变;
- 如果当前的操作为 “./“:继续停留在当前文件夹,此时 depth 保持不变;
- 如果当前的操作为 “x/“:移动到下一层名为 x 的子文件夹中。则此时将 depth 加 1。
最终返回当前的文件层次深度 depth 即可。
1 | class Solution: |
1 | class Solution { |
1 | class Solution { |
1 | public class Solution { |
1 | int minOperations(char ** logs, int logsSize) { |
1 | var minOperations = function(logs) { |
1 | func minOperations(logs []string) (depth int) { |
复杂度分析
时间复杂度:O(n),其中 n 为字符串数组的长度。只需遍历一遍字符串数组即可。
空间复杂度:O(1)。
Comments