如果一棵二叉树满足下述几个条件,则可以称为 奇偶树 :
- 二叉树根节点所在层下标为
0 ,根的子节点所在层下标为 1 ,根的孙节点所在层下标为 2 ,依此类推。
- 偶数下标 层上的所有节点的值都是 奇 整数,从左到右按顺序 严格递增
- 奇数下标 层上的所有节点的值都是 偶 整数,从左到右按顺序 严格递减
给你二叉树的根节点,如果二叉树为 奇偶树 ,则返回 true ,否则返回 false 。
示例 1:
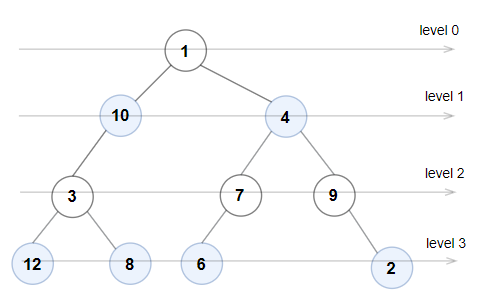
**输入:** root = [1,10,4,3,null,7,9,12,8,6,null,null,2]
**输出:** true
**解释:** 每一层的节点值分别是:
0 层:[1]
1 层:[10,4]
2 层:[3,7,9]
3 层:[12,8,6,2]
由于 0 层和 2 层上的节点值都是奇数且严格递增,而 1 层和 3 层上的节点值都是偶数且严格递减,因此这是一棵奇偶树。
示例 2:
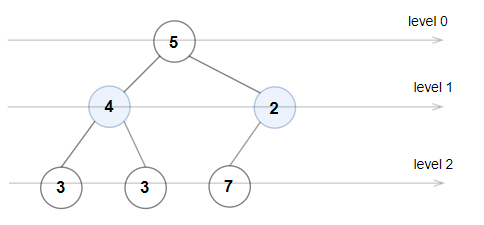
**输入:** root = [5,4,2,3,3,7]
**输出:** false
**解释:** 每一层的节点值分别是:
0 层:[5]
1 层:[4,2]
2 层:[3,3,7]
2 层上的节点值不满足严格递增的条件,所以这不是一棵奇偶树。
示例 3:
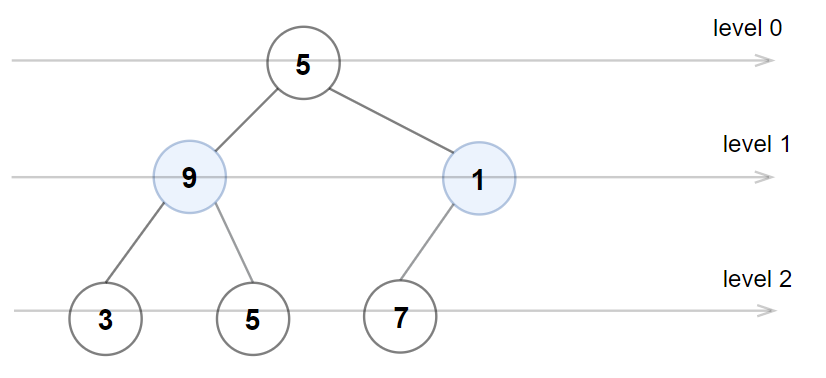
**输入:** root = [5,9,1,3,5,7]
**输出:** false
**解释:** 1 层上的节点值应为偶数。
示例 4:
**输入:** root = [1]
**输出:** true
示例 5:
**输入:** root = [11,8,6,1,3,9,11,30,20,18,16,12,10,4,2,17]
**输出:** true
提示:
- 树中节点数在范围
[1, 105] 内
1 <= Node.val <= 106
方法一:广度优先搜索
由于判断一棵二叉树是否为奇偶树的条件是针对同一层的节点,因此可以使用广度优先搜索,每一轮搜索访问同一层的全部节点,且只会访问这一层的节点。
使用队列存储节点。初始时,将根节点加入队列。每一轮搜索之前,队列中的节点是同一层的全部节点,记队列的大小为 size,该轮搜索只访问 size 个节点,即可保证该轮搜索访问的恰好是同一层的全部节点。搜索过程中,将当前层的节点的非空子节点依次加入队列,用于下一层的搜索。
判断一棵二叉树是否为奇偶树,需要考虑两个条件,一是节点值的奇偶性,二是节点值的单调性,这两个条件都由层下标的奇偶性决定。因此,需要维护搜索到的层下标,以及对于每一层搜索都需要维护上一个节点值。
如果当前层下标是偶数,则要求当前层的所有节点的值都是奇数,且节点值从左到右严格递增。如果遇到节点值是偶数,或者当前节点值小于等于上一个节点值,则二叉树一定不是奇偶树。
如果当前层下标是奇数,则要求当前层的所有节点的值都是偶数,且节点值从左到右严格递减。如果遇到节点值是奇数,或者当前节点值大于等于上一个节点值,则二叉树一定不是奇偶树。
如果二叉树的所有节点都满足奇偶树的条件,则二叉树是奇偶树。
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution {
public boolean isEvenOddTree(TreeNode root) {
Queue<TreeNode> queue = new ArrayDeque<TreeNode>();
queue.offer(root);
int level = 0;
while (!queue.isEmpty()) {
int size = queue.size();
int prev = level % 2 == 0 ? Integer.MIN_VALUE : Integer.MAX_VALUE;
for (int i = 0; i < size; i++) {
TreeNode node = queue.poll();
int value = node.val;
if (level % 2 == value % 2) {
return false;
}
if ((level % 2 == 0 && value <= prev) || (level % 2 == 1 && value >= prev)) {
return false;
}
prev = value;
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
level++;
}
return true;
}
}
|
[sol1-C#]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| public class Solution {
public bool IsEvenOddTree(TreeNode root) {
Queue<TreeNode> queue = new Queue<TreeNode>();
queue.Enqueue(root);
int level = 0;
while (queue.Count > 0) {
int size = queue.Count;
int prev = level % 2 == 0 ? int.MinValue : int.MaxValue;
for (int i = 0; i < size; i++) {
TreeNode node = queue.Dequeue();
int value = node.val;
if (level % 2 == value % 2) {
return false;
}
if ((level % 2 == 0 && value <= prev) || (level % 2 == 1 && value >= prev)) {
return false;
}
prev = value;
if (node.left != null) {
queue.Enqueue(node.left);
}
if (node.right != null) {
queue.Enqueue(node.right);
}
}
level++;
}
return true;
}
}
|
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| class Solution {
public:
bool isEvenOddTree(TreeNode* root) {
queue<TreeNode*> qu;
qu.push(root);
int level = 0;
while (!qu.empty()) {
int size = qu.size();
int prev = level % 2 == 0 ? INT_MIN : INT_MAX;
for (int i = 0; i < size; i++) {
TreeNode * node = qu.front();
qu.pop();
int value = node->val;
if (level % 2 == value % 2) {
return false;
}
if ((level % 2 == 0 && value <= prev) || (level % 2 == 1 && value >= prev)) {
return false;
}
prev = value;
if (node->left != nullptr) {
qu.push(node->left);
}
if (node->right != nullptr) {
qu.push(node->right);
}
}
level++;
}
return true;
}
};
|
[sol1-Python3]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution:
def isEvenOddTree(self, root: Optional[TreeNode]) -> bool:
queue = [root]
level = 0
while queue:
prev = float('inf') if level % 2 else 0
nxt = []
for node in queue:
val = node.val
if val % 2 == level % 2 or level % 2 == 0 and val <= prev or level % 2 == 1 and val >= prev:
return False
prev = val
if node.left:
nxt.append(node.left)
if node.right:
nxt.append(node.right)
queue = nxt
level += 1
return True
|
[sol1-JavaScript]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| var isEvenOddTree = function(root) {
const queue = [];
queue.push(root);
let level = 0;
while (queue.length) {
const size = queue.length;
let prev = level % 2 == 0 ? -Number.MAX_VALUE : Number.MAX_VALUE;
for (let i = 0; i < size; i++) {
const node = queue.shift();
const value = node.val;
if (level % 2 === value % 2) {
return false;
}
if ((level % 2 === 0 && value <= prev) || (level % 2 === 1 && value >= prev)) {
return false;
}
prev = value;
if (node.left) {
queue.push(node.left);
}
if (node.right) {
queue.push(node.right);
}
}
level++;
}
return true;
};
|
[sol1-C]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| #define MAX_SIZE 100001
bool isEvenOddTree(struct TreeNode* root){
struct TreeNode* qu[MAX_SIZE];
int head = 0, tail = 0;
qu[head++] = root;
int level = 0;
while (tail < head) {
int size = head - tail;
int prev = level % 2 == 0 ? INT_MIN : INT_MAX;
for (int i = 0; i < size; i++) {
struct TreeNode * node = qu[tail++];
int value = node->val;
if (level % 2 == value % 2) {
return false;
}
if ((level % 2 == 0 && value <= prev) || (level % 2 == 1 && value >= prev)) {
return false;
}
prev = value;
if (node->left != NULL) {
qu[head++] = node->left;
}
if (node->right != NULL) {
qu[head++] = node->right;
}
}
level++;
}
return true;
}
|
[sol1-Golang]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| func isEvenOddTree(root *TreeNode) bool {
q := []*TreeNode{root}
for level := 0; len(q) > 0; level++ {
prev := 0
if level%2 == 1 {
prev = math.MaxInt32
}
size := len(q)
for _, node := range q {
val := node.Val
if val%2 == level%2 || level%2 == 0 && val <= prev || level%2 == 1 && val >= prev {
return false
}
prev = val
if node.Left != nil {
q = append(q, node.Left)
}
if node.Right != nil {
q = append(q, node.Right)
}
}
q = q[size:]
}
return true
}
|
复杂度分析