1621-大小为 K 的不重叠线段的数目

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:45:43 2023-09-13 16:45:43 Updated    

给你一维空间的 n 个点，其中第 i 个点（编号从 0 到 n-1）位于 x = i 处，请你找到 恰好 k
个不重叠 线段且每个线段至少覆盖两个点的方案数。线段的两个端点必须都是 整数坐标 。这 k 个线段不需要全部覆盖全部 n
个点，且它们的端点 可以 重合。

请你返回 k 个不重叠线段的方案数。由于答案可能很大，请将结果对 109 + 7 取余 后返回。

示例 1：

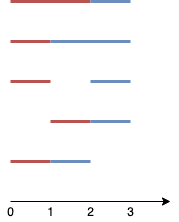
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/10/17/ex1.png)

**输入：** n = 4, k = 2
**输出：** 5
**解释：** 如图所示，两个线段分别用红色和蓝色标出。
上图展示了 5 种不同的方案 {(0,2),(2,3)}，{(0,1),(1,3)}，{(0,1),(2,3)}，{(1,2),(2,3)}，{(0,1),(1,2)} 。

示例 2：

**输入：** n = 3, k = 1
**输出：** 3
**解释：** 总共有 3 种不同的方案 {(0,1)}, {(0,2)}, {(1,2)} 。

示例 3：

**输入：** n = 30, k = 7
**输出：** 796297179
**解释：** 画 7 条线段的总方案数为 3796297200 种。将这个数对 109 + 7 取余得到 796297179 。

示例 4：

**输入：** n = 5, k = 3
**输出：** 7

示例 5：

**输入：** n = 3, k = 2
**输出：** 1

提示：

  • 2 <= n <= 1000
  • 1 <= k <= n-1

方法一：动态规划

思路与算法

记 f[i][j] 表示使用 0 .. i 的点构造了 j 条线段的方案数。我们需要区分第 j 条线段的右端点是否就是 i，因此可以考虑把 f[i][j] 拆分成两个状态：

  • f[i][j][0] 表示第 j 条线段的右端点不是 i，也就是说我们没有办法继续延长第 j 条线段；

  • f[i][j][1] 表示第 j 条线段的右端点就是 i，也就是说我们可以选择是否继续延长第 j 条线段。

如何进行状态转移呢？

首先考虑 f[i][j][0]，因为第 j 条线段的右端点不是 i，因此第 i 个点没有用上，那么 0 .. i-1 的点构造了 j 条线段，即

f[i][j][0] = f[i-1][j][0] + f[i-1][j][1]

再考虑 f[i][j][1]，因为第 j 条线段的右端点就是 i，因此有两种情况：

  • 第 j 条线段长度为 1，那么 0 .. i-1 的点构造了 j-1 条线段，即

    f[i][j][1] = f[i-1][j-1][0] + f[i-1][j-1][1]

  • 第 j 条线段长度大于 1，那么删去第 j 条线段 i-1 .. i 的这一部分，0 .. i-1 的点仍然构造了 j 条线段，并且点 i-1 是属于第 j 条线段的，即

    f[i][j][1] = f[i-1][j][1]

加上边界条件 f[0][0][0] = 1，最终答案即为 f[n-1][k][0] + f[n-1][k][1]。

注意事项

力扣对 C++ 不是很友好，编译时只开 -O1 优化，所以直接拿 vector<> 定义三维数组很容易超时。下面给出两种解决方法。

代码

第一种是定义数组，每次动态规划之前记得清空一下。

[sol11-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
private:
    static constexpr int mod = 1000000007;
    int f[1000][1001][2];

public:
    int numberOfSets(int n, int k) {
        memset(f, 0, sizeof(f));
        f[0][0][0] = 1;
        for (int i = 1; i < n; ++i) {
            for (int j = 0; j <= k; ++j) {
                f[i][j][0] = (f[i - 1][j][0] + f[i - 1][j][1]) % mod;
                f[i][j][1] = f[i - 1][j][1];
                if (j > 0) {
                    f[i][j][1] += f[i - 1][j - 1][0];
                    f[i][j][1] %= mod;
                    f[i][j][1] += f[i - 1][j - 1][1];
                    f[i][j][1] %= mod;
                }
            }
        }
        return (f[n - 1][k][0] + f[n - 1][k][1]) % mod;
    }
};

第二种是使用 vector<> 定义 pair<int, int> 的二维数组。

[sol12-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
private:
    static constexpr int mod = 1000000007;
public:
    int numberOfSets(int n, int k) {
        vector<vector<pair<int, int>>> f(n, vector<pair<int, int>>(k + 1));
        f[0][0].first = 1;
        for (int i = 1; i < n; ++i) {
            for (int j = 0; j <= k; ++j) {
                f[i][j].first = (f[i - 1][j].first + f[i - 1][j].second) % mod;
                f[i][j].second = f[i - 1][j].second;
                if (j > 0) {
                    f[i][j].second += f[i - 1][j - 1].first;
                    f[i][j].second %= mod;
                    f[i][j].second += f[i - 1][j - 1].second;
                    f[i][j].second %= mod;
                }
            }
        }
        return (f[n - 1][k].first + f[n - 1][k].second) % mod;
    }
};

复杂度分析

  • 时间复杂度：O(nk)。

  • 空间复杂度：O(nk)。

方法二：组合数学

思路与算法

本方法参考自某不愿透露姓名的太阳神。

题目等价于求出满足

0 \leq l_1 < r_1 \leq l_2 < r_2 \leq \cdots \leq l_k < r_k < n

的 (l_1, \cdots, l_k, r_1, \cdots, r_k) 的数目。

令 l’_i = l_i + (i-1) 以及 r’_i = r_i + (i-1)，(l’_1, \cdots, l’_k, r’_1, \cdots, r’_k) 与 (l_1, \cdots, l_k, r_1, \cdots, r_k) 逐一对应，并且满足

0 \leq l’_1 < r’_1 < l’_2 < r’_2 < \cdots < l’_k < r’_k < n+k-1

此时就可以使用组合求解方案数了，即在 [0, n+k-1) 共 n+k-1 个数中选择 2k 个，因此答案为

\binom{n+k-1/2k}

代码

[sol2-Python3]
1
2
3
class Solution:
    def numberOfSets(self, n: int, k: int) -> int:
        return math.comb(n + k - 1, k * 2) % (10**9 + 7)

复杂度分析

  • 时间复杂度：用了 Python 的高精度，就当是 O(k) 吧。

  • 空间复杂度：O(1)。

 Comments
On this page
1621-大小为 K 的不重叠线段的数目