1627-带阈值的图连通性

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:28 2023-09-13 16:06:28 Updated    

有 n 座城市，编号从 1 到 n 。编号为 x 和 y 的两座城市直接连通的前提是： x 和 y 的公因数中，至少有一个
严格大于 某个阈值 threshold 。更正式地说，如果存在整数 z ，且满足以下所有条件，则编号 x 和 y
的城市之间有一条道路：

  • x % z == 0
  • y % z == 0
  • z > threshold

给你两个整数 n 和 threshold ，以及一个待查询数组，请你判断每个查询 queries[i] = [ai, bi] 指向的城市
ai 和 bi 是否连通（即，它们之间是否存在一条路径）。

返回数组 answer ，其中answer.length == queries.length 。如果第 i 个查询中指向的城市 ai 和
bi 连通，则 answer[i] 为 true ；如果不连通，则 answer[i] 为 false 。

示例 1：

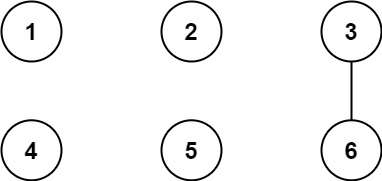
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/10/18/ex1.jpg)

**输入：** n = 6, threshold = 2, queries = [[1,4],[2,5],[3,6]]
**输出：** [false,false,true]
**解释：** 每个数的因数如下：
1:   1
2:   1, 2
3:   1, **3**
4:   1, 2, **4**
5:   1, **5**
6:   1, 2, **3** , **6**
所有大于阈值的的因数已经加粗标识，只有城市 3 和 6 共享公约数 3 ，因此结果是： 
[1,4]   1 与 4 不连通
[2,5]   2 与 5 不连通
[3,6]   3 与 6 连通，存在路径 3--6

示例 2：

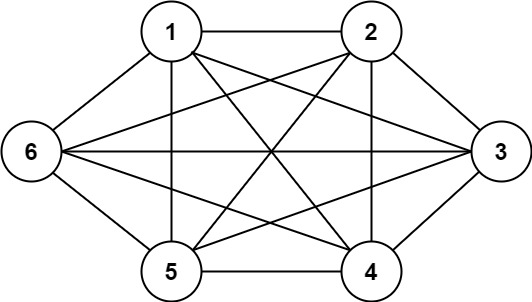
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/10/18/tmp.jpg)

**输入：** n = 6, threshold = 0, queries = [[4,5],[3,4],[3,2],[2,6],[1,3]]
**输出：** [true,true,true,true,true]
**解释：** 每个数的因数与上一个例子相同。但是，由于阈值为 0 ，所有的因数都大于阈值。因为所有的数字共享公因数 1 ，所以所有的城市都互相连通。

示例 3：

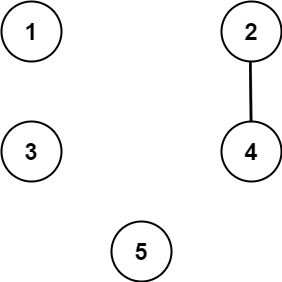
![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2020/10/16/ex3.jpg)

**输入：** n = 5, threshold = 1, queries = [[4,5],[4,5],[3,2],[2,3],[3,4]]
**输出：** [false,false,false,false,false]
**解释：** 只有城市 2 和 4 共享的公约数 2 严格大于阈值 1 ，所以只有这两座城市是连通的。
注意，同一对节点 [x, y] 可以有多个查询，并且查询 [x，y] 等同于查询 [y，x] 。

提示：

  • 2 <= n <= 104
  • 0 <= threshold <= n
  • 1 <= queries.length <= 105
  • queries[i].length == 2
  • 1 <= ai, bi <= cities
  • ai != bi

解法

思路和算法

这道题要求计算每个查询中的两个城市是否属于同一个连通分量。如果两个城市的编号有大于阈值 threshold 的公因数，则两个城市之间有一条道路连通。对于同一个连通分量，其中的每个城市的编号都至少和该连通分量中的另一个城市的编号有大于阈值 threshold 的公因数。

连通性问题可以使用并查集解决。由于两个城市合并的条件是两个城市的编号有大于阈值 threshold 的公因数，因此应将每个城市的编号和自身的所有大于阈值 threshold 的因数合并，则两个有大于阈值 threshold 的公因数的编号对应的城市将合并到同一个连通分量。

由于有 n 个城市，编号从 1 到 n，因此创建大小为 n + 1 的并查集，包含 0 到 n 的所有整数。并查集初始化时，每个整数分别属于不同的集合。初始化之后，遍历大于 threshold 且小于等于 n 的每个整数，将该整数和自身的所有不超过 n 的倍数合并，遍历结束之后，得到所有连通分量。

得到所有连通分量之后，对于每个查询 query，如果 query}[0] 和 query}[1] 属于同一个连通分量则查询结果为 true，否则查询结果为 false。

代码

[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class Solution {
    public List<Boolean> areConnected(int n, int threshold, int[][] queries) {
        UnionFind uf = new UnionFind(n + 1);
        for (int i = threshold + 1; i * 2 <= n; i++) {
            for (int j = i * 2; j <= n; j += i) {
                uf.union(i, j);
            }
        }
        List<Boolean> answer = new ArrayList<Boolean>();
        for (int[] query : queries) {
            answer.add(uf.find(query[0]) == uf.find(query[1]));
        }
        return answer;
    }
}

class UnionFind {
    private int[] parent;
    private int[] rank;

    public UnionFind(int n) {
        parent = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
        rank = new int[n];
    }

    public void union(int x, int y) {
        int rootx = find(x);
        int rooty = find(y);
        if (rootx != rooty) {
            if (rank[rootx] > rank[rooty]) {
                parent[rooty] = rootx;
            } else if (rank[rootx] < rank[rooty]) {
                parent[rootx] = rooty;
            } else {
                parent[rooty] = rootx;
                rank[rootx]++;
            }
        }
    }

    public int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }
}
[sol1-C#]
1

复杂度分析

  • 时间复杂度：O(n \log n \times \alpha(n) + m \times \alpha(n))，其中 n 是数组 nums 的长度，m 是数组 queries 的长度，\alpha 是反阿克曼函数。并查集的初始化需要 O(n) 的时间，合并操作的总次数是 O(n \log n)，查询操作的总次数是 O(m)，这里的并查集使用了路径压缩和按秩合并，每次操作的时间是 O(\alpha(n))，因此时间复杂度是 O(n \log n \times \alpha(n) + m \times \alpha(n))。

  • 空间复杂度：O(n)，其中 n 是数组 nums 的长度。并查集需要 O(n) 的空间。注意返回值不计入空间复杂度。

 Comments
On this page
1627-带阈值的图连通性
  1. 解法
    1. 思路和算法
    2. 代码
    3. 复杂度分析